Cách xét tính liên tục của hàm số và bài tập áp dụng

Xét tính liên tục của hàm số là một khái niệm quan trọng trong chương trình toán 11, đặc biệt là trong giải tích và lý thuyết hàm.

Để xét tính liên tục của một hàm số, chúng ta cần kiểm tra ba điều kiện chính: tồn tại giá trị hàm tại điểm x, giới hạn của hàm khi x tiến đến giá trị x0 tồn tại và bằng giới hạn của hàm tại điểm x0. Nếu ba điều kiện này được thỏa mãn, ta nói rằng hàm số là liên tục tại điểm x0.

Trong bài viết này, thayphu sẽ tìm hiểu về cách xét tính liên tục của hàm số và vận dụng giải một số dạng bài tập mẫu liên quan.

Lý thuyết về hàm số liên tục

Hàm số liên tục tại 1 điểm

• Cho hàm số y = f(x) đã xác định trên khoảng (a;b) và x0 ∈ (a;b). Hàm số y = f(x) được gọi là hàm số liên tục tại xo nếu

xx0f(x)=f(x0)

• Hàm số f(x0) nếu không liên tục tại điểm xo thì được gọi là điểm gián đoạn của hàm số f(x).

Hàm số liên tục trên 1 khoảng

• Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
• Hàm số y = f(x) được gọi là liên tục trên đoạn [a,b] nếu nó liên tục trên khoảng (a,b) và

xa+f(x)=f(a),xxb-f(x)=f(b)

Các dạng bài tập xét tính liên tục và phương pháp giải

Dạng 1: Xét tính liên tục của hàm số tại 1 điểm

Phương pháp:

• Bước 1: Tính f(x0)
• Bước 2: Tính xx0f(x) hoặc xx0+f(x), xx0-f(x)
• Bước 3: So sánh: xx0f(x) hoặc xx0+f(x), xx0-f(x) với f(x0)
  • Nếu xx0f(x) = f(x0) hoặc xx0+f(x) = xx0-f(x) = f(x0) thì kết luận hàm số liên tục tại x0.
  • Nếu xx0f(x) không tồn tại hoặc xx0f(x) f(x0) thì kết luận hàm số không liên tục tại x0.
• Bước 4: Kết luận.

Ví dụ:

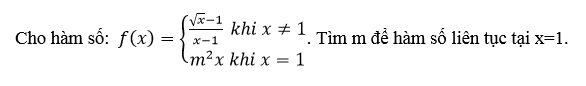
Gợi ý lời giải:

Hàm đã cho xác định trên [0;+)

Ta có f(1)=m2

x1x-1x-1=x11x+1=12

Để hàm số liên tục tại x=1 thì x1f(x)=f(1)m2=12

m=12=22

Vậy m=22.

Dạng 2: Xét tính liên tục của hàm số trên 1 khoảng, 1 đoạn

Để xác định tính liên tục của hàm số trên khoảng [a, b] hoặc đoạn (a, b), chúng ta cần kiểm tra tính liên tục của hàm số tại mọi điểm trong khoảng, đoạn đó. Điều này có nghĩa là hàm số f(x) phải là liên tục tại các điểm x thuộc [a, b] hoặc (a, b).

Phương pháp:

• Bước 1: Xác định miền xác định của hàm số đã cho. Có nghĩa là chúng ta cần đảm bảo rằng khoảng hoặc đoạn được xét thuộc miền xác định của hàm số đã cho.
• Bước 2: Kiểm tra tính xác định của hàm số trên khoảng hoặc đoạn: Kiểm tra xem hàm số có được định nghĩa trên toàn bộ khoảng hoặc đoạn không. Điều này đảm bảo rằng hàm số tồn tại và xác định tại mọi điểm trong khoảng hoặc đoạn.
• Bước 3: Kiểm tra tính liên tục tại các điểm trong khoảng hoặc đoạn đã cho.
• Bước 4: Kết luận.

Ví dụ: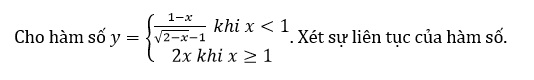

Gợi ý lời giải:

Hàm số xác định và liên tục trên (-;1) và (1;+).

Từ đó suy ra, ta cần xét tính liên tục của hàm số tại x=1

f(1)=2.1=2

x1f(x)=x11=x2-x-1

=x1(1-x) (2-x+1)2-x-1

=x1(2-x+1)=2

Ta thấy x1f(x)=f(1) nên hàm số liên tục tại x=1.

Vậy hàm số liên tục trên R.

Dạng 3: Xét tính liên tục của hàm số để chứng minh phương trình có nghiệm.

Phương pháp:

• Bước 1: Xác định phương trình có nghiệm: Đầu tiên, hãy xác định phương trình có nghiệm trên một khoảng hoặc đoạn cụ thể.
• Bước 2: Dựa vào để bài, tìm hai số a và b (a<b) thỏa mãn điều kiện f(a).f(b)<0. Khi đó, phương trình f(x)=0 có ít nhất là một nghiệm
• Bước 3: Kết luận.

Ví dụ: Chứng minh rằng phương trình (1-m2) x5-3x-1=0 luôn có nghiệm với mọi m.

Gợi ý lời giải:

Xét hàm số f(x)=(1-m2) x5-3x-1

Ta có: f(0)=-1 và f(-1)=m2+1

nên f(-1).f(0)=-(m2+1)<0, mR

Mặt khác: f(x)=f(x)=(1-m2) x5-3x-1 là hàm đa thức nên liên tục trên [-1;0]

Suy ra, phương trình (1-m2) x5-3x-1=0 có ít nhất 1 nghiệm thuộc (-1;0).

Vậy phương trình (1-m2) x5-3x-1=0 luôn có nghiệm với mọi m.

Bài viết trên đã giới thiệu về khái niệm tính liên tục của hàm số, các dạng bài tập mẫu và gợi ý cách giải các dạng bài. Qua đó, chúng ta đã thấy cách xét tính liên tục của hàm số và vận dụng vào các dạng bài tập.

Để nắm vững khái niệm này, chúng ta cần thực hành nhiều bài tập và đọc thêm tài liệu để hiểu rõ hơn về tính liên tục của các hàm số phức tạp hơn. Mong rằng bài viết này của thayphu.net sẽ giúp các bạn hiểu rõ hơn về tính liên tục của hàm số và các dạng bài tập liên quan.