Cách giải bất phương trình bậc nhất hai ẩn kèm bài tập áp dụng

Bất phương trình bậc nhất hai ẩn dạng thuộc toán học cơ bản lớp 10, bạn có thể tìm hiểu cách giải bất phương trình bật nhất 2 ẩn và bài tập áp dụng tại đây.

Bất phương trình bậc nhất hai ẩn dạng toán học khá phổ biến được tích hợp vào chương trình giảng dạy trên giảng đường hiện nay. Các dạng bài tập liên quan đến bất phương trình này kèm theo lời giải chi tiết đã được trình bày trong bài viết dưới đẩy của thayphu. Tham khảo để nắm được kiến thức liên quan đến phương trình bậc nhất có 2 ẩn và cách giải bạn nhé!

Kiến thức bất phương trình bậc nhất hai ẩn

Bất phương trình bậc nhất hai ẩn có dạng tổng quát như sau: ax + by ≤ c.

Trong đó:

• a,b,c chính là 3 số đã cho trước (a, b khác 0)

• x, y là 2 ẩn số mà bạn cần tìm được

Các cặp số (x0; y0) sẽ là các cặp nghiệm của bất phương trình bậc nhất 2 ẩn ax + by ≤ c, sao cho thỏa mãn được điều kiện ax0 + by0 ≤ c.

Miền nghiệm là gì?

• Định nghĩa miền nghiệm là gì?

Là tập hợp tất cả điểm trong mặt phẳng Oxy sẽ có tọa độ chính là nghiệm của bất phương trình hai ẩn hay còn được gọi là miền nghiệm của bất phương trình đó.

• Định lý miền nghiệm

Cho đường thẳng (d) có dạng ax + by + c = 0 chia mặt phẳng tọa độ Oxy thành 2 nửa mặt phẳng sao cho trong đó có 1 trong 2 mặt phẳng ấy gồm các điểm có tọa độ thỏa mãn ax + by + c > 0, nữa còn lại gồm các điểm có tọa độ thỏa mãn ax + by + c < 0.

Suy ra nửa mặt phẳng là miền nghiệm của bất phương trình hai ẩn ax + by + c > 0 là nghiệm của bất phương trình đó.

• Cách biểu diễn miền nghiệm của bất phương trình bậc nhất 2 ẩn được hướng dẫn chi tiết dưới đây.

Hướng dẫn cách biểu diễn miền nghiệm của bất phương trình bậc nhất 2 ẩn

Thế nào là một bất phương trình bậc nhất hai ẩn

• Trong một mặt phẳng tọa độ, ta gọi tập hợp các điểm có tọa độ thỏa mãn mọi bất phương trình là miền nghiệm.

• Để có thể xác định được miền nghiệm của hệ, ta có thể dùng phương pháp biểu diễn hình học như sau:

• Với mỗi bất phương trình ta xác định miền nghiệm của hệ và gạch bỏ miền còn lại.

• Sau khi làm tất cả với các phương trình trong hệ trên cùng một mặt phẳng tọa độ, miền nghiệm còn lại không bị gạch chính là nghiệm của bất phương trình.

Bài tập áp dụng phương trình bậc nhất 2 ẩn có lời giải

Bài tập 1

Trong các cặp số (-1 ; 5), (2 ; -3), (4 ; 2) cặp số nào là nghiệm của phương trình bậc nhất 2 ẩn: 5x – 2y = 16.

Giải:

• x = -1, y = 5 => 5x – 2y = -5 – 10 = -15, vì vậy (-1 ; 5) không là nghiệm của phương trình 5x – 2y = 16.

• x = 2, y = -3 => 5x – 2y = 10 + 6 = 16, vì vậy (2 ; -3) là nghiệm của phương trình 5x – 2y = 16.

• x = 4, y = 2 => 5x – 2y = 20 – 4 = 16, vì vậy (4 ; 2) là nghiệm của phương trình 5x – 2y = 16.

Bài tập 2

Cho biết (-4 ; 2) là một nghiệm của bất phương trình hai ẩn -2x + 2my = 3m + 1, hãy xác nhận giá trị của m.

Giải:

Vì (-4 ; 2) là một nghiệm của bất phương trình 2 ẩn -2x + 2my = 3m + 1 => 8 + 4m = 3m + 1. Từ đó suy ra m = 1 – 8 = -7.

Bài tập 3

Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau: -x + 2 + 2(y – 2) < 2(1 – x).

Giải:

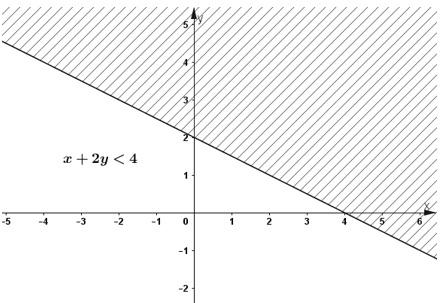
–x + 2 + 2(y – 2) < 2(1 – x) => –x + 2 + 2y – 4 < 2 – 2x => x + 2y < 4 (1)

Biểu diễn tập nghiệm của bất phương trình 2 ẩn trên mặt phẳng tọa độ :

• Vẽ đường thẳng x + 2y = 4.

• Thay tọa độ (0; 0) vào (1) ta được 0 + 0 < 4

=> (0; 0) chính là một nghiệm của bất phương trình.

Vậy miền nghiệm của bất phương trình 2 ẩn là nửa mặt phẳng chứa gốc tọa độ không kể bờ với bờ là đường thẳng x + 2y = 4 (miền không bị gạch).

Bài tập 4

Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau: 3(x – 1) + 4(y – 2) < 5x – 3.

Giải:

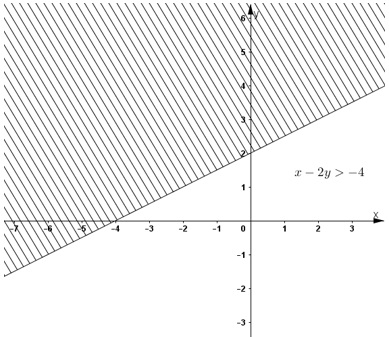
3(x – 1) + 4(y – 2) < 5x – 3 => 3x – 3 + 4y – 8 < 5x – 3 => -2x + 4y < 8 => x – 2y > –4 ( chia cả hai vế cho -2 < 0)

Biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ:

• Vẽ đường thẳng x – 2y = –4.

• Thay tọa độ (0; 0) vào (2) ta được: 0 + 0 > –4 đúng

=> (0; 0) là một nghiệm của bất phương trình.

Vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa gốc tọa độ không kể bờ với bờ là đường thẳng x – 2y = –4

4 bài tập cơ bản về bất phương trình bậc nhất 2 ẩn đã được liệt kê và giải chi tiết để bạn tham khảo và nắm được cách giải thông qua nội dung được trình bày. Hy vọng với cách giải trên bạn có thể hiểu và áp dụng vào các bài tập toán tương tự.

Kết luận

Với những kiến thức về bất phương trình bậc nhất 2 ẩn kèm theo một vài bài tập có lời giải sẽ giúp bạn hiểu hơn về dạng phương trình này. Học toán là cả một quá trình tiếp thu và phân tích tư duy để đưa đến kết quả chính xác cuối cùng. Chúc bạn học nhanh hiểu nhanh thông qua nội dung về kiến thức toán được chia sẻ ở nội dung bài viết trên.