Công thức tính khoảng cách giữa 2 điểm trong mặt phẳng oxy và oxyz

Chia sẻ cách công thức tính khoảng cách giữa 2 điểm trong mặt phẳng oxy và oxyz chuẩn nhất, đây là kiến thức toán lớp 10 cơ bản mà bạn cần nắm.

Công thức tính khoảng cách giữa cách giữa 2 điểm là một kiến thức cơ bản trong toán hình học lớp 10 và cũng là một công thức được áp dụng rộng rãi trong hình học không gian. Nhiều bạn thắc mắc rằng khoảng cách giữa hai điểm trên mặt phẳng hay không gian có sự khác nhau về công thức hay không? Hãy cùng thayphut.net theo dõi bài viết dưới đây để có đáp án cho mình nhé.

Khoảng cách giữa hai điểm là gì?

Tìm hiểu khoảng cách giữa hai điểm là gì?

Khoảng cách giữa hai điểm là một khái niệm quan trọng trong hình học và các lĩnh vực liên quan. Nó cho chúng ta biết khoảng cách từ một điểm đến điểm khác, giúp đo lường khoảng cách giữa các vật thể, đặc biệt là trong không gian Euclid. Khoảng cách giữa hai điểm được sử dụng trong rất nhiều bài toán thực tế, như tính tốc độ, vận tốc, độ lớn và độ chính xác của các vật thể.

Khoảng cách giữa hai điểm cũng đóng vai trò quan trọng trong xử lý hình ảnh và đồ họa máy tính. Trong các ứng dụng này, khoảng cách giữa hai điểm được sử dụng để tính toán và phân tích các hình dạng khác nhau của vật thể, đánh giá các thuộc tính như kích thước, hình dạng và khoảng cách. Khoảng cách giữa hai điểm cũng được sử dụng trong các bài toán liên quan đến nhận dạng hình ảnh, phân tích khuôn mặt và các bài toán khác trong lĩnh vực trí tuệ nhân tạo.

Khoảng cách giữa hai điểm còn được sử dụng trong địa chất, đặc biệt là trong đo lường độ sâu của các giếng khoan dầu và khí tự nhiên. Khoảng cách giữa hai điểm cũng là một yếu tố quan trọng trong xác định tọa độ của các địa danh trên bản đồ và hệ thống định vị toàn cầu. Trong các ứng dụng y tế, khoảng cách giữa hai điểm được sử dụng để đo khoảng cách giữa các cơ quan trong cơ thể, đánh giá kích thước và hình dạng của các khối u và các vật thể khác.

Công thức tính khoảng cách giữa 2 điểm trong toán lớp 10

Ở lớp 10 thì chúng ta sẽ được học 2 công thức để tính khoảng cách 2 điểm. Đầu tiên là tính khoảng cách trong mặt phẳng Oxy và thứ hai là tính khoảng cách trong mặt phẳng Oxyz. Cả hai công thức này đều sẽ sử dụng công thức định lý Pythagoras để tính khoảng cách.

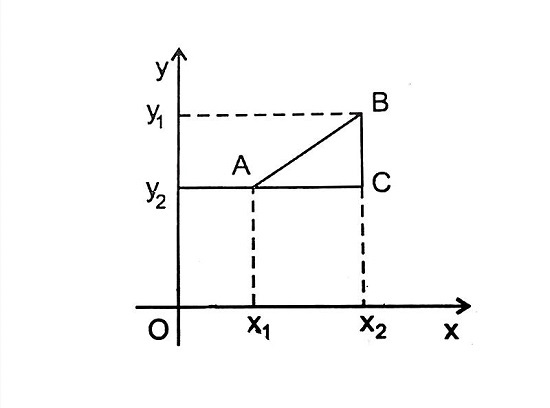
Tính khoảng cách giữa hai điểm trong mặt phẳng

Tính khoảng cách của 2 điểm trong mặt phẳng Oxy

Để tính khoảng cách giữa hai điểm trong mặt phẳng Oxy, ta có thể sử dụng công thức sau:

Khoảng cách giữa hai điểm trên mặt phẳng Oxy có A(x1, y1) và B(x2, y2) được tính bằng công thức:

Trong đó, d là khoảng cách giữa hai điểm A và B, và (x1, y1) và (x2, y2) lần lượt là tọa độ của hai điểm A và B trên mặt phẳng Oxy.

Ví dụ, nếu ta muốn tính khoảng cách giữa hai điểm A(3, 4) và B(7, 8) trên mặt phẳng Oxy, ta sẽ áp dụng công thức trên và có:

Do đó, khoảng cách giữa hai điểm A và B trên mặt phẳng Oxy là khoảng 5,657 đơn vị.

Tính khoảng cách của 2 điểm trong mặt phẳng Oxyz

Để tính khoảng cách giữa hai điểm trong mặt phẳng Oxyz, ta có thể sử dụng công thức sau:

Khoảng cách giữa hai điểm A(x1, y1, z1) và B(x2, y2, z2) được tính bằng công thức:

Trong đó, d là khoảng cách giữa hai điểm A và B, và (x1, y1, z1) và (x2, y2, z2) lần lượt là tọa độ của hai điểm A và B trên mặt phẳng Oxyz.

Ví dụ, nếu ta muốn tính khoảng cách giữa hai điểm A(1, 2, 3) và B(4, 5, 6) trên mặt phẳng Oxyz, ta sẽ áp dụng công thức trên và có:

Do đó, khoảng cách giữa hai điểm A và B trên mặt phẳng Oxyz là khoảng 5,196 đơn vị.

So sánh hai công thức trên ta có thể thấy rằng công thức đầu tiên chỉ có hoành độ và tung độ. Ở công thức thứ hai thì có thêm cao độ. Cả hai công thức đều căn bậc 2 và cách tính của hai công thức trên đều như nhau. Như vậy ta chỉ cần nhớ rằng “Khoảng cách giữa 2 điểm bằng tổng bình phương cuối trừ bình phương đầu rồi lấy căn bậc 2”.

Tùy vào dữ kiện mà đề bài cho, dạng bài cũng như các kiến thức hình học thì dựa vào đó mà bạn có thể tìm được tọa độ điểm để có thể tính độ dài đoạn thẳng nối giữa hai điểm trên mặt phẳng.

Ví dụ khi tính khoảng cách giữa 2 điểm khi đề bài cho hai điểm A(x1, y1) và B(x2, y2) trên hình tròn, ta sử dụng công thức:

Trong đó, d là khoảng cách giữa hai điểm A và B. Lưu ý: Nếu đề bài cho hình tròn có bán kính R và tâm là điểm A(x1, y1), ta cần tìm khoảng cách giữa một điểm bất kỳ P(x2, y2) và tâm C, ta sử dụng công thức:

Trong đó, d là khoảng cách giữa điểm P và tâm C của hình tròn có bán kính R.

Lời kết

Như vậy cách tính khoảng cách giữa 2 điểm có công thức đơn giản và vô cùng dễ nhớ. Đây là kiến thức cơ bản mà bạn cần nắm chắc khi giải bài tập. Đặc biệt khi giải bài với dữ kiện nhiều hơn thì bạn cần vận dụng nhiều kiến thức hơn mới có thể tìm ra hướng giải đúng.