Cách giải bất phương trình chứa căn - toán lớp 10

Bất phương trình chứa căn có nhiều dạng bài khó, thường có trong kì thi HSG. Nắm chắc công thức giải bất phương trình chứa căn sẽ giúp bạn giải toán dễ dàng

Bất phương trình hay bất phương trình chứa căn là một nội dung quan trọng trong chương trình toán lớp 10. Để giải tốt các dạng bài này, yêu cầu người học phải rèn luyện thật kỹ càng và giải càng nhiều bài tập càng tốt. Thông thường những câu hỏi liên quan đến bất phương trình thường xuất hiện trong kì thi lớn như tốt nghiệp THPT nên chúng ta cần lưu ý hơn.

Hãy cùng theo dõi bài viết dưới đây của thayphu để biết đâu là cách giải phương trình chứa căn nhé.

Công thức giải bất phương trình chứa căn lớp 10

Bất phương trình chứa căn là một nội dung quan trọng

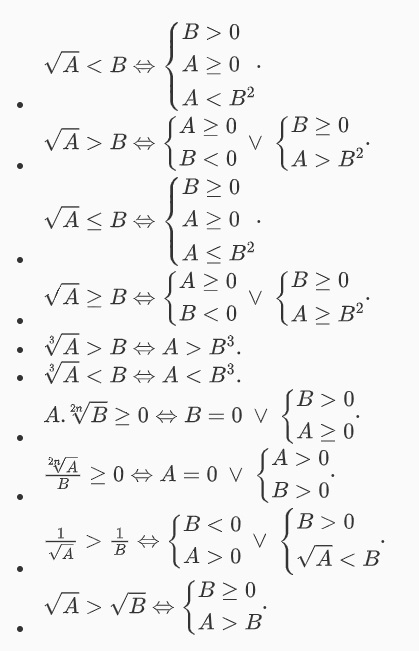
Phương pháp giải bất phương trình chứa căn

Cách giải bất phương trình chứa căn toán lớp 10

Để giải bất phương trình chứa căn lớp 10, ta cần áp dụng những nguyên tắc chung sau đây:

• Bỏ qua dấu căn để đưa bất phương trình về dạng đơn giản hơn.
• Giải bất phương trình đã được đưa về dạng đơn giản hơn bằng các phương pháp giải bất phương trình thông thường.
• Kiểm tra kết quả và đáp án để đảm bảo rằng chúng thỏa mãn điều kiện dấu căn.

Bất phương trình chứa căn cơ bản

Ví dụ 1: Giải các bất phương trình sau đây:

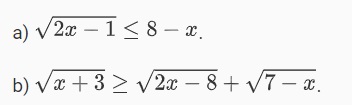
Cách giải:

1. Bất phương trình đã cho sẽ tương đương với

Như vậy tập nghiệm của bất phương trình sẽ là

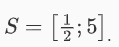
2. Đối với câu này, ta có điều kiện như sau:

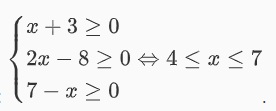
Bất phương trình chứa căn đã cho tương đương với

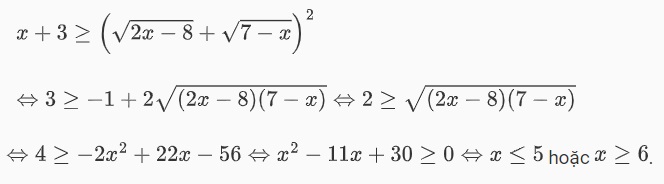
Như vậy, tập nghiệm của bất phương trình đó chính là: 4 <= x <=5 hoặc 6 <=x <=7.

Ví dụ 2: Cho các bất phương trình dưới đây, tìm tập nghiệm S của phương trình:

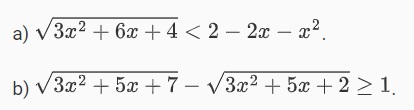
Cách giải:

1. Đặt t là vế bên trái với điều kiện là t>=0. Cụ thể là 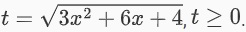Lúc này ta suy ra được là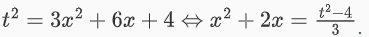

Bất phương trình đã cho tương đương với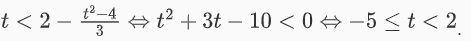

Vì t >= 0, kết hợp với bất phương trình trên, ta có điều kiện chung đó là 0 <= t < 2.

Với điều kiện trên, ta được,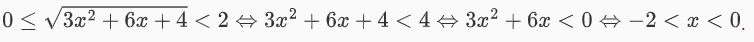

Như vậy, tập nghiệm của phương trình sẽ là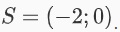

Sử dụng phương pháp chia khoảng & tách căn khi giải bất phương trình

Ví dụ: Tìm nghiệm của bất phương trình sau đây:

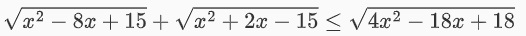
Cách giải:

Khi nhận đề như dạng bất phương trình trên, ta sẽ xét nghiệm của cả 3 phương trình. Sau khi tìm nghiệm của 3 phương trình, ta nhận thấy x = 3 là nghiệm chung. Chính vì vậy mà việc bạn cần làm đó chính là tách căn, sau đó đặt thừa số chung. Lời giải chi tiết sẽ là:

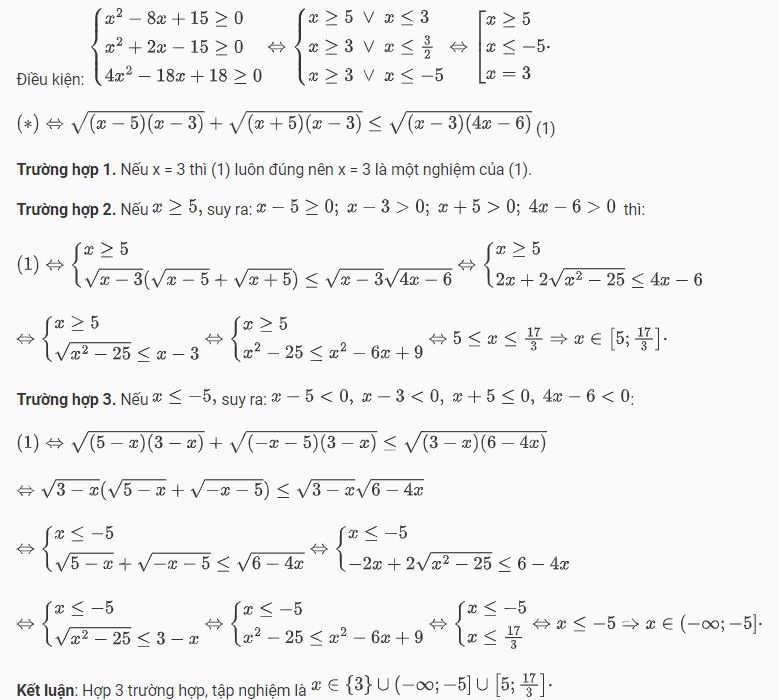
Đặt ẩn phụ khi giải bất phương trình chứa căn

Ví dụ: Giải các bất phương trình sau đây:

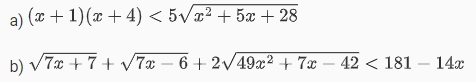
Cách giải:

1. Bất phương trình đã cho sẽ tương đương với

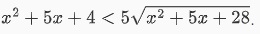
Ta đặt Phương trình này tương đương với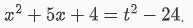

Bất phương trình lúc này sẽ trở thành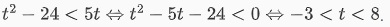

Vì t có điều kiện là t >= 0 nên ta có điều kiện chung là 0 <= t <8.

Suy ra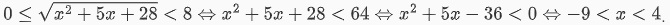

Như vậy tập nghiệm của phương trình sẽ là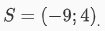

2. Làm đơn giản bất phương trình, ta được:

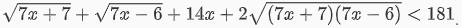
Phương trình có điều kiện như sau:

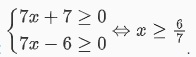(1)

Đặt biến t =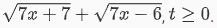

Ta suy ra được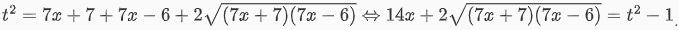

Bất phương trình lúc này sẽ trở thành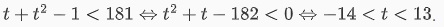

Vì là t >= 0 nên 0 <= t <13.

Với điều kiện trên, ta được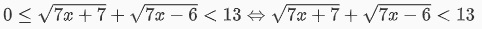

Phương trình tương đương với:

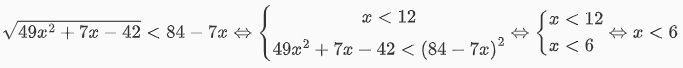(2)

Từ (1) và (2), ta suy ra được nghiệm của bất phương trình là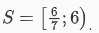

Sử dụng phương pháp đánh giá để giải bất phương trình

Ví dụ: Giải bất phương trình sau đây:

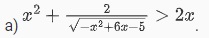
Cách giải:

Với điều kiện 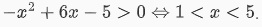, ta được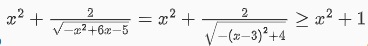

Tối giản bất phương trình, ta có bất phương trình tương đương là x^2 + 1 >= 2x. Dấu “=” lúc này chỉ xảy ra khi x = 1. Chính vì vậy mà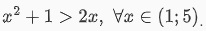

Như vậy tập nghiệm của phương trình sẽ là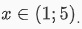

Những lưu ý khi giải bất phương trình chứa căn

Các lưu ý khi giải bất phương trình chứa căn

Khi giải bất phương trình chứa căn lớp 10, có một số lưu ý sau đây cần được lưu ý:

• Điều kiện dấu căn: Khi bỏ qua dấu căn để đưa bất phương trình về dạng đơn giản hơn, ta phải đảm bảo rằng các giá trị của biểu thức bên trong căn không âm. Nếu không, phép tính căn sẽ không xác định và phương trình sẽ không có nghiệm.

• Phép toán bên trong căn: Trong quá trình giải bất phương trình, ta cần thực hiện các phép toán như bình phương, cộng trừ, nhân chia... với biểu thức có chứa căn. Tuy nhiên, cần phải kiểm tra kỹ trước khi thực hiện phép toán để đảm bảo rằng các giá trị của biểu thức đó vẫn đảm bảo điều kiện dấu căn.

• Kết quả có thể không chính xác: Do tính đặc biệt của căn lớp 10, kết quả có thể không chính xác hoặc phức tạp. Để đảm bảo tính chính xác của kết quả, ta nên kiểm tra lại bằng cách đưa giá trị đã tìm được vào bất phương trình ban đầu.

• Đối xứng: Nếu bất phương trình có dạng f(x) > 0 hoặc f(x) < 0, ta có thể sử dụng tính chất đối xứng của đồ thị để giải quyết bài toán. Tức là nếu f(a) > 0 thì f(b) > 0, với $b$ là giá trị đối xứng của a qua trục đứng của đồ thị.

• Thay thế biến số: Đôi khi, ta có thể sử dụng phép thay thế biến số để đưa bất phương trình về dạng đơn giản hơn. Việc này giúp giải quyết bài toán dễ dàng hơn, tuy nhiên, cần phải kiểm tra lại kết quả cuối cùng.

Một số bài tập áp dụng bất phương trình chứa căn

Sau khi đọc bài học trên của thayphu.net, hi vọng các bạn đã nắm chắc những lý thuyết, các công thức cũng như các dạng bài tập. Từ những kiến thức này, bạn sẽ vận dụng thật tốt trong việc giải toán. Đừng quên luyện tập thường xuyên về dạng bài bất phương trình chứa căn để có hiệu quả tốt nhất nhé.