Cách viết phương trình đường thẳng đi qua 2 điểm

Phương trình đường thẳng đi qua 2 điểm là kiến thức cơ bản cần nhớ trong toán lớp 10. thầy phú sẽ giúp bạn củng cố và chuẩn bị tốt cho các kì thi sắp tới.

Bắt đầu vào kiến thức trung học phổ thông chắc hẳn nhiều bạn còn gặp nhiều khó khăn khi phải tiếp thu những kiến thức hoàn toàn mới. Trong số đó, phương trình đường thẳng đi qua 2 điểm được khá nhiều bạn học quan tâm. Chính vì vậy mà ngay trong bài viết này, thayphu.net sẽ hướng dẫn bạn cách xác định cũng như viết phương trình đường thẳng một cách chi tiết nhất.

Phương trình tham số của đường thẳng có dạng gì?

Tìm hiểu phương trình tham số của đường thẳng có dạng gì

Phương trình tham số của đường thẳng là một cách khác để mô tả một đường thẳng trên mặt phẳng, thường được sử dụng trong đại số tuyến tính. Phương trình sẽ được viết dưới dạng như sau:

x = x₁ + at

y = y₁ + bt

Trong đó:

• (x₁, y₁) là một điểm trên đường thẳng, gọi là điểm gốc (hay điểm đầu tiên)

• a và b là hằng số thực, được gọi là các tham số của đường thẳng

• t là một biến thực, cho phép di chuyển trên đường thẳng bằng cách thay đổi giá trị của nó.

Phương trình tham số của đường thẳng cho phép biểu diễn đường thẳng dưới dạng hệ số và hệ số góc, cũng như tính toán các đặc tính khác của đường thẳng, bao gồm vị trí của các điểm trên đường thẳng, khoảng cách giữa hai điểm trên đường thẳng, và góc giữa hai đường thẳng.

Dạng của phương trình tổng quát đường thẳng

Phương trình tổng quát của đường thẳng là một phương trình tuyến tính có dạng: Ax + By + C = 0

Trong đó:

• A, B và C là các hằng số thực và không đồng thời bằng 0.

• x và y là các biến đại diện cho các điểm trên đường thẳng.

Nếu phương trình tổng quát của đường thẳng được viết dưới dạng Ax + By + C = 0, ta có thể tìm độ dốc của đường thẳng bằng cách chia hệ số A cho B (nếu B không bằng 0), hoặc tìm hệ số góc của đường thẳng bằng cách tính arctan của độ dốc. Ngoài ra, vị trí của điểm cắt trục tung có thể được tính bằng cách đặt x = 0 trong phương trình tổng quát của đường thẳng, trong khi vị trí của điểm cắt trục hoành có thể được tính bằng cách đặt y = 0 trong phương trình.

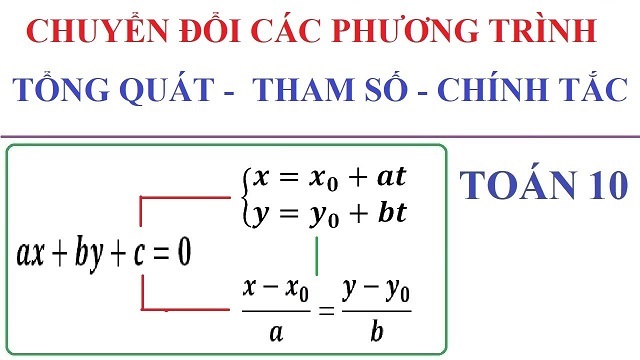
Cách chuyển phương trình tổng quát sang các dạng khác

Ví dụ 1: Cho đường thẳng AB với A(-2, 3) và B(4, -1). Hãy tìm phương trình tổng quát của đường thẳng AB.

Để tìm phương trình tổng quát của đường thẳng, ta có thể sử dụng hệ số góc của đường thẳng:

Độ dốc của đường thẳng AB: m = (yB - yA)/(xB - xA) = (-1 - 3)/(4 - (-2)) = -0.5

Vì A(-2, 3) là một điểm trên đường thẳng AB, ta có thể sử dụng điểm này để tìm hệ số b của đường thẳng: y = mx + b => 3 = -0.5(-2) + b => b = 2

Phương trình tổng quát của đường thẳng AB là: y = -0.5x + 2, hoặc có thể viết lại dưới dạng tổng quát: 0.5x + y - 2 = 0.

Ví dụ 2: Cho phương trình tổng quát của đường thẳng là 2x - 3y + 6 = 0. Tìm vị trí của các điểm cắt của đường thẳng với trục hoành và trục tung.

Để tìm vị trí của điểm cắt trục hoành và trục tung, ta có thể đặt x = 0 và y = 0 tương ứng vào phương trình tổng quát của đường thẳng:

Điểm cắt trục tung: x = 0, 2x - 3y + 6 = 0 => y = 2

Điểm cắt trục hoành: y = 0, 2x - 3y + 6 = 0 => x = 3

Vậy đường thẳng có điểm cắt trục tung là (0, 2) và điểm cắt trục hoành là (3, 0).

Cách viết phương trình đường thẳng đi qua 2 điểm

Hướng dẫn cách viết phương trình đường thẳng đi qua 2 điểm

Để viết phương trình đường thẳng đi qua hai điểm đã biết trên mặt phẳng tọa độ, ta có thể sử dụng công thức sau đây:

Phương trình đường thẳng đi qua hai điểm P(x1, y1) và Q(x2, y2) là:

(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)

hoặc bạn cũng có thể viết lại phương trình thành:

(y2 - y1)x + (x1 - x2)y + x2y1 - x1y2 = 0

Ví dụ, để tìm phương trình đường thẳng đi qua hai điểm P(1, 2) và Q(3, 4), ta có thể sử dụng công thức trên để có được:

(y2 - y1)x + (x1 - x2)y + x2y1 - x1y2 = (4 - 2)x + (1 - 3)y + 3(2) - 1(4) = 2x - 2y + 2 = 0

Vậy phương trình đường thẳng đi qua hai điểm P(1, 2) và Q(3, 4) là 2x - 2y + 2 = 0.

Cách viết phương trình đường thẳng đi qua 2 điểm thuộc trục tọa độ

Nếu hai điểm thuộc trục tọa độ, thì phương trình đường thẳng đi qua chúng có thể được dễ dàng xác định. Cụ thể:

• Nếu hai điểm là (a, 0) và (b, 0) (với a < b), thì đường thẳng đi qua chúng là trục hoành, có phương trình đơn giản là y = 0.

• Nếu hai điểm là (0, a) và (0, b) (với a < b), thì đường thẳng đi qua chúng là trục tung, có phương trình đơn giản là x = 0.

• Nếu một điểm nằm trên trục Ox có tọa độ (a;0) và một điểm nằm trên trục Oy có tọa độ (0;b), thì để tìm phương trình đường thẳng đi qua hai điểm đó, ta sử dụng công thức: x/a + y/b = 1.

Bài tập áp dụng

Bài tập 1: Viết phương trình đường thẳng đi qua hai điểm A(2, 5) và B(2, -3).

Vì hai điểm A và B có cùng tọa độ x, nên đường thẳng đi qua chúng là một đường thẳng song song với trục y và có phương trình x = 2.

Bài tập 2: Viết phương trình đường thẳng đi qua hai điểm A(-4, 6) và B(2, 6).

Đường thẳng đi qua hai điểm A và B là đường thẳng vuông góc với trục tung và có phương trình y = 6.

Bài tập 3: Viết phương trình đường thẳng đi qua hai điểm A(1, 3) và B(-2, 4).

Để viết phương trình đường thẳng đi qua hai điểm A và B, ta sử dụng công thức:

(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)

Thay giá trị của hai điểm A(1, 3) và B(-2, 4) vào công thức, ta được:

(y - 3)/(4 - 3) = (x - 1)/(-2 - 1)

Rút gọn ta được:

(y - 3) = (-1/3)(x - 1)

Kết luận ta được phương trình đường thẳng đi qua hai điểm A và B: 3x + y = 10.

Như vậy trên đây bài viết đã giới thiệu cho các bạn về cách viết phương trình đường thẳng đi qua 2 điểm. Mong rằng qua những gì đã chia sẻ thì các bạn đọc đã nắm được những kiến thức chính và vận dụng nó hiệu quả vào việc giải bài tập trong toán lớp 10. Chúc tất cả các bạn học tập thật tốt. Đừng quên thường xuyên cập nhật các bài viết của chúng tôi để biết thêm những thông tin bổ ích nhé.