Công thức tính tiệm cận đứng và bài tập áp dụng nhanh nhất

Tìm hiểu khái niệm tiệm cận đứng, tìm tiệm cận đứng chính xác nhất bằng công thức và máy tính cầm tay, kèm bài tập áp dụng.

Tiệm cận đứng là một kiến thức cơ bản và cũng dạng bài chúng ta thường gặp ở các bài thi. Đây là một kiến thức không quá khó nhưng nếu không nắm chắc thì bạn sẽ đánh mất số điểm mà không đáng có. Chính vì vậy trong bài viết này, thayphu.net sẽ tổng hợp lại các kiến thức liên quan và ví dụ các bài tập minh họa cho các bạn tham khảo.

Tiệm cận đứng là gì?

Tiệm cận đứng là khái niệm trong giải tích, được sử dụng để mô tả hành vi của một hàm số khi giá trị đầu vào tiến đến một giá trị xác định mà không bao giờ đạt được giá trị đó. Nó được gọi là "cận đứng" bởi vì đường cong của hàm số tiến đến một giá trị xác định và "đứng" vì nó không bao giờ chạm hoặc cắt qua giá trị đó.

Cụ thể, giả sử f(x) là một hàm số và x0 là một giá trị xác định. Nếu khi x tiến đến x0, giá trị của f(x) tiến đến vô cùng hoặc âm vô cùng mà không bao giờ đạt được giá trị đó, thì ta nói rằng f(x) có tiệm cận đứng tại x0. Ta có điều kiện như sau:

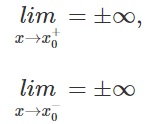
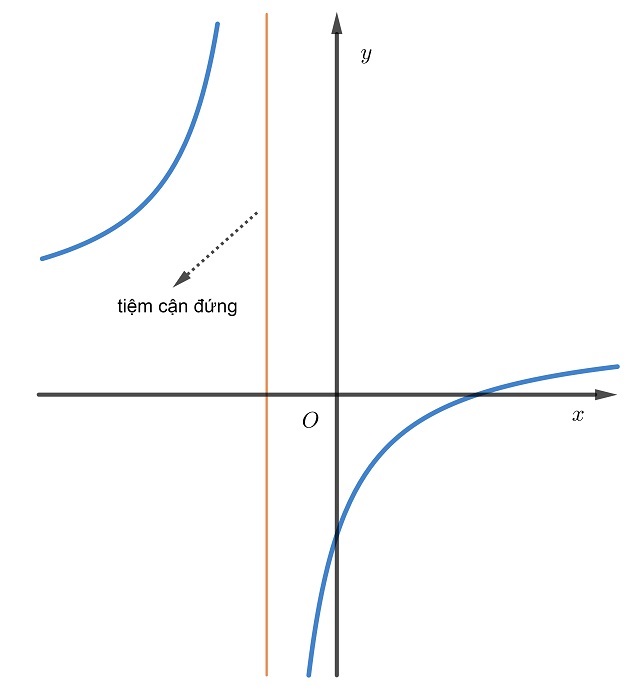
Khái quát tìm tiệm cận đứng là gì?

Tiệm cận đứng có thể là một đường thẳng ngang hoặc dạng vô hạn, phụ thuộc vào hành vi của hàm số gần giá trị x0. Việc hiểu rõ về tiệm cận đứng là rất quan trọng trong việc giải quyết nhiều bài toán và ứng dụng trong toán học và khoa học tự nhiên.

Các bước tìm tiệm cận đứng của một hàm số

Để tìm tiệm cận đứng của một hàm số có dạng f(x)/g(x), ta thực hiện theo các bước sau đây:

• Bước 1: Đầu tiên bạn tìm nghiệm của phương trình g(x).

• Bước 2: Đối với những nghiệm mà bạn vừa tìm được, nếu trùng với nghiệm của f(x) thì loại ngay.

• Bước 3: Với những nghiệm còn lại, thì đường thẳng x = x0 sẽ là tiệm cận đứng của hàm số đã cho.

Ví dụ: Tìm tiệm cận đứng của hàm số y = x2−1 / x2−3x+2

Cách giải:

Ta xét phương trình: g(x) = 0 ⇔ x2−3x+2=0. Lúc này ta được 2 nghiệm x =1 hoặc x = 2.

Trong 2 nghiệm trên, x = 1 cũng là nghiệm của f(x). Tức là nghiệm của phương trình x2−1 = 0. Và x = 2 không phải là nghiệm của phương trình x2−1=0

Chính vì vậy mà ta có thể kết luận rằng, hàm số đã cho ở đều bài có tiệm cận đứng là x = 2.

Ví dụ: Tìm tiệm cận đứng của hàm số f(x) = 2x^3 - 4x^2 + 5x - 7

Để tìm tiệm cận đứng của hàm số này, ta làm theo các bước sau:

Tính giới hạn của hàm số f(x) khi x tiến đến vô cùng hoặc âm vô cùng:

Khi x tiến đến vô cùng, ta có: f(x) = 2x^3 - 4x^2 + 5x - 7 -> vô cùng

Khi x tiến đến âm vô cùng, ta có: f(x) = 2x^3 - 4x^2 + 5x - 7 -> âm vô cùng

Vì giới hạn không tồn tại hoặc bằng vô cùng, ta phải kiểm tra xem hàm số có thể được viết dưới dạng f(x) = kx + b với k và b là các hằng số không đổi khi x tiến đến vô cùng hay không.

Ta có f(x) = 2x^3 - 4x^2 + 5x - 7 = 2x^3(1 - 2x/x + 5/(2x^2) - 7/(2x^3))

Vì khi x tiến đến vô cùng, các giá trị 2x/x, 5/(2x^2), 7/(2x^3) đều tiến đến 0, nên ta có thể xấp xỉ hàm số f(x) = 2x^3(1 - 2x/x + 5/(2x^2) - 7/(2x^3)) bằng f(x) = 2x^3(1 - 0 + 0 - 0) = 2x^3

Vậy, ta có thể viết hàm số f(x) = 2x^3 dưới dạng f(x) = kx + b với k = 0 và b = 0. Do đó, phương trình của tiệm cận đứng là x = 0.

Vậy, tiệm cận đứng của hàm số f(x) là x = 0.

Hướng dẫn tìm tiệm cận đứng bằng máy tính cầm tay

Để tìm tiệm cận đứng của một hàm số f(x)/g(x) bằng máy tính thì ta cũng thực hiện như các bước ở phần trước. Đầu tiên ta sẽ đi tìm nghiệm của hàm số g(x) rồi bước tiếp theo loại những nghiệm của hàm số f(x). Cụ thể bạn thực hiện các bước sau:

• Bước 1: Bạn sử dụng tính năng SOLVE trên máy tính để giải nghiệm. Nếu mẫu số của hàm số đã cho có căn bậc 2 hoặc căn bậc 3 thì bạn có thể dùng Equation ( EQN) để tìm nghiệm của phương trình.

• Bước 2: Sử dụng nút CALC để thử các nghiệm của mẫu số mà bạn vừa tìm được. Bạn sẽ tiến hành thử nghiệm của mẫu có phải là nghiệm của tử số hay không.

• Bước 3: Những nghiệm x0 nào là nghiệm của mẫu số nhưng không là nghiệm của tử số thì x=x0 chính là đường tiệm cận đứng của hàm số.

Ví dụ: Tìm tiệm cận đứng của hàm số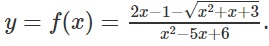

Đầu tiên tính nghiệm của phương trình: x2-5x + 6=0.

Trên máy tính của bạn ta sẽ bấm lần lượt Mode -> 5 -> 3 để giải phương trình bậc 2.

Sau đó bạn bấm lần lượt hệ số 1, -5, 6 và nhấn bằng.

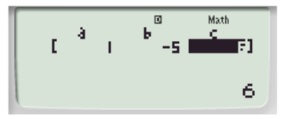
Lúc này màn hình xuất hiện 2 nghiệm đó chính là x=2 và x=3.

Sau đó tiến hành nhập tử số vào máy tính cầm tay

Sử dụng tính năng CALC rồi thay từng giá trị x=2 và x=3 vào tử số.

Sau khi thử nghiệm ta nhận thấy rằng x=2 thì tử số bằng 0 và x=3 thì tử số khác 0.

Kết luận: x=3 là tiệm cận đứng của hàm số.

Tìm tiệm cận đứng dựa vào bảng biến thiên hàm số

• Bước 1: Bạn dựa vào bảng biến thiên để tìm tập xác định của hàm số.

• Bước 2: Bạn tiến hành quan sát bảng biến thiên. Tiệm cận đứng của hàm số là những điểm mà tại giá trị này hàm số không xác định.

• Bước 3: Kết luận tiệm cận đứng của hàm số.

Một số bài tập áp dụng

Dạng 1: Tìm tiệm cận đứng dựa vào định nghĩa

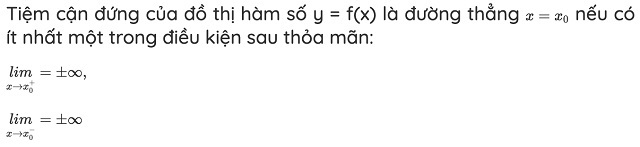
Tiệm cận đứng dựa vào định nghĩa

Ví dụ: Cho đồ thị hàm số và tìm tiệm cận đứng của hàm số.

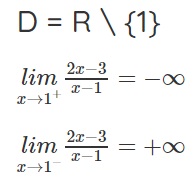
Dạng 2: Tìm tiệm cận đứng của đồ thị hàm số phân thức

Với những gì chia sẻ trong bài viết trên sẽ giúp bạn nắm được tiệm cận đứng là gì và biết được cách tìm tiệm cận đứng chuẩn xác nhất.