Cách tìm tiệm cận ngang của đồ thị hàm số và bài tập áp dụng

Thế nào là Tiệm cận ngang? Tiệm cận ngang của đồ thị hàm số là đường thẳng như thế nào? Các công thức và các dạng bài tập Tiệm cận ngang.

Trong chương trình toán học THPT, đặc biệt là các kỳ thi toán 12, các bạn học sinh thường gặp các bài toán tiệm cận ngang. Tùy dạng toán này không khó nhưng đòi hỏi các bạn phải nắm chắc kiến thức để vận dụng vào bài tập một cách tốt nhất, nhanh nhất. Bài viết dưới đây của thayphu.net sẽ tổng hợp đầy đủ lý thuyết, công thức, cách tìm tiệm cận ngang của đồ thị hàm số và các dạng bài tập.

Khái niệm đường Tiệm cận ngang

Cho đồ thị hàm số y = f(x) xác định trên (a; +∞)là:

Nếu lim x→+∞ y = b thì y = b là đường tiệm cận ngang của đồ thị hàm số y = f (x).

Tương tự, cho đồ thị hàm số y = f(x) xác định trên (a; -∞)là:

Nếu lim x→-∞ y = b thì y = b là đường tiệm cận ngang của đồ thị hàm số y = f (x).

Vậy hàm số sẽ có tối đa là hai đường tiệm cận ngang hoặc tối thiểu không có đường tiệm cận ngang nào.

​

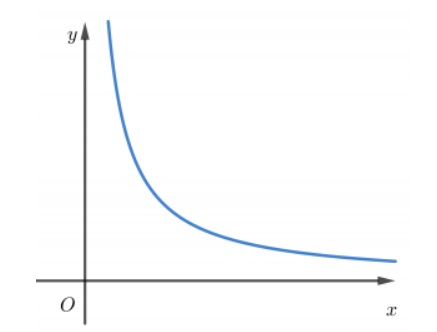
Cách tìm Tiệm cận ngang của đồ thị hàm số

Để tìm tiệm cận ngang của một đồ thị hàm số, ta có các bước sau:

Bước 1: Ta tìm tập xác định của hàm số.

Bước 2: Tính giới hạn của hàm số đó tại vô cực (nếu có). Từ đó ta xác định được đường tiệm cận ngang.

Giải: Tập xác định hàm số là: D = R

Ta có: lim x→-∞ y = 0, lim x→+∞ y = 0

Vậy đồ thị hàm số có đúng một đường tiệm cận ngang là y = 0.

Các công thức tính tiệm cận ngang

Tiệm cận ngang của đồ thị hàm số ac:

Công thức tính Tiệm cận ngang của hàm phân thức hữu tỉ:

Công thức tính Tiệm cận ngang của hàm phân thức vô tỉ:

Cách tính tiệm cận ngang bằng máy tính casio

Hướng dẫn:

Tìm đường tiệm cận ngang bằng máy tính, ta sẽ tính giá trị gần đúng của lim x→+∞y và lim x→-∞y.

Tính lim x→+∞y: Ta tính giá trị của hàm số tại một giá trị x rất lớn. Ta lấy x = 10^9 . Kết quả là giá trị gần đúng của lim x→+∞y.

Tính lim x→-∞y: Ta tính giá trị của hàm số tại một giá trị x rất nhỏ. Ta lấy x = - 10^9. Kết quả là giá trị gần đúng của lim x→-∞y.

=> Tính giá trị hàm số tại một giá trị x, ta dùng chức năng CALC trên máy tính.

Ví dụ:

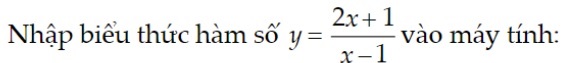
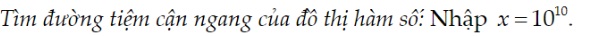
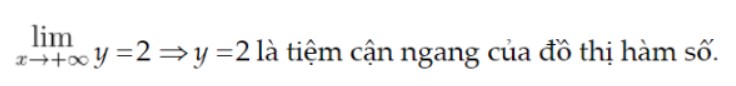
Các bài tập tiệm cận ngang

Trên đây đã tổng hợp đầy đủ nội dung kiến thức và các dạng bài tập về đường tiệm cận ngang. Mong rằng với những nội dung kiến thức trên sẽ mang lại hữu ích cho các bạn.