Các trường hợp bằng nhau của hai tam giác và bài tập vận dụng

Có 3 trường hợp bằng nhau của hai tam giác gồm cạnh - cạnh - cạnh, cạnh - góc - cạnh và góc - cạnh - góc. Nắm vững lý thuyết này các em dễ dàng làm tốt bài tập.

Các trường hợp bằng nhau của hai tam giác là gì? Bài viết sau đây thayphu sẽ hệ thống lại kiến thức, các dạng bài tập liên quan và phương pháp giải. Đây sẽ là tài liệu hữu ích, giúp các em ôn tập và học tốt nội dung Toán 7 này!

Các trường hợp bằng nhau của hai tam giác

Lý thuyết trường hợp bằng nhau của hai tam giác

Trường hợp bằng nhau cạnh - cạnh - cạnh (c.c.c)

Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì 2 tam giác đó bằng nhau.

Xét 2 tam giác ABC và A’B’C’ có:

AB = A’B’; AC = A’C’; BC = B’C’

Thì ABC = A’B’C’ (c.c.c)

Trường hợp bằng nhau cạnh - góc - cạnh (c.g.c)

Nếu 2 cạnh và góc xen giữa của tam giác này lần lượt bằng 2 cạnh và góc xen giữa của tam giác kia thì 2 tam giác đó bằng nhau.

• Nếu AB = A’B’, A = A', AC = A’C’ thì ABC = A’B’C’ (c.g.c)

Ví dụ minh họa:

Chỉ cần thêm 1 điều kiện thì 2 tam giác dưới đây trong các trường hợp dưới đây sẽ bằng nhau theo trường hợp cạnh - góc - cạnh. Hãy nêu điều kiện đó tương ứng cho mỗi hình.

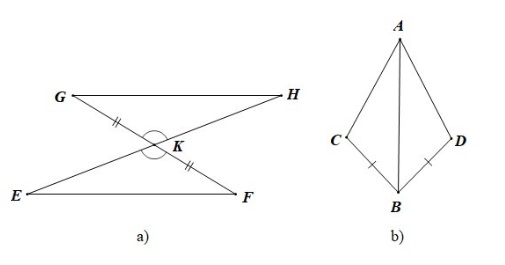
Cách giải:

1. Xét 2 tam giác KGH VÀ KEF ta có: GKH = EKF (đối đỉnh) và KG = KF

Để KGH = KEF theo trường hợp cạnh - góc - cạnh thì điều kiện còn thiếu là góc xen giữa 2 cặp cạnh bằng nhau.

Mà GKH của KGH xen giữa 2 cạnh KG và KH

EKF của KEF xen giữa 2 cạnh KE và KF

=> Điều kiện còn thiếu là KH = KE

Vậy để KGH = KEF theo cạnh - góc - cạnh thì cần thêm điều kiện là KH = KE.

2. Xét 2 ABC và ABD ta có: BC = BD và AB là cạnh chung

Để ABC = ABD bằng nhau theo trường hợp cạnh - góc - cạnh thì điều kiện còn thiếu là về góc sao cho cặp góc bằng nhau là góc xen giữa 2 cặp cạnh bằng nhau.

Ta lại có: - Góc xen giữa 2 cạnh BC và BA của ABC là ABC

• Góc xen giữa 2 cạnh BD và BA của ABD là ABD

=> Điều kiện còn thiếu là ABC = ABD.

Trường hợp bằng nhau góc - cạnh - góc (g.c.g)

Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 cạnh và 2 góc kề của tam giác kia thì 2 tam giác đó bằng nhau.

Nếu ABC và A’B’C’ có: BC = B’C’; B = B'; C = C'

Thì ABC = A’B’C’ (g.c.g)

Các trường hợp bằng nhau của hai tam giác vuông

Các trường hợp bằng nhau của tam giác vuông

Hai cạnh góc vuông

Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng 2 cạnh góc vuông của tam giác kia thì 2 tam giác vuông đó bằng nhau (cạnh - góc - cạnh).

Cạnh góc vuông và góc nhọn kề cạnh đó

Nếu 1 cạnh góc vuông và 1 góc nhọn kề cạnh ấy của tam giác vuông này bằng 1 cạnh góc vuông và 1 góc nhọn kề cạnh ấy của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau (góc - cạnh - góc).

Cạnh huyền - góc nhọn

Nếu cạnh huyền và 1 góc nhọn của tam giác vuông này bằng cạnh huyền và 1 góc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau (góc - cạnh - góc).

Cạnh huyền - cạnh góc vuông

Nếu cạnh huyền và 1 cạnh góc vuông của tam giác vuông này bằng cạnh huyền và 1 cạnh góc vuông của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.

Ví dụ minh họa:

Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC. Hãy chứng minh rằng AHB = AHC.

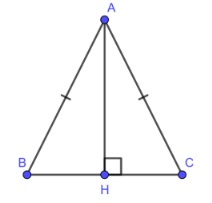
Cách giải:

Ta có ABC cân tại A và AH là đường cao của ABC

=> AH là đường trung tuyến của ABC

=> BH = CH

Xét 2 AHB và AHC có:

• AHB = AHC = 90 độ

• AB = AC (giả thiết)

• BH = CH (cmt)

=> AHB = AHC (cạnh huyền - cạnh góc vuông)

Các dạng bài tập về trường hợp bằng nhau của hai tam giác

Dạng 1 - Tìm hoặc chứng minh 2 tam giác bằng nhau

Phương pháp giải:

• Đầu tiên là xét 2 tam giác

• Sau đó kiểm tra 3 điều kiện bằng nhau cạnh - cạnh - cạnh, cạnh - góc - cạnh, góc - cạnh - góc.

• Cuối cùng là kết luận 2 tam giác bằng nhau.

Bài tập vận dụng:

Cho góc nhọn xOy có tia Oz là tia phân giác. Qua điểm A thuộc tia Ox ta vẽ đường thẳng song song với Oy cắt Oz tại điểm M. Qua điểm M kẻ đường thẳng song song với Ox cắt Oy tại điểm B.

1. Chứng minh OAM = MBO

2. Từ M vẽ MH Ox; MK Oy, chứng minh MHO = MKO

Cách giải:

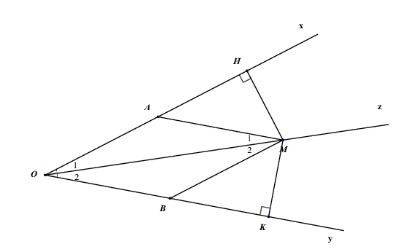
1. Xét 2 OAM và MBO ta có:

• O1 = M1 (2 góc so le trong)

• OM là cạnh chung

• M2 = O2 (2 góc so le trong)

=> OAM = MBO (g.c.g)

2. Ta có: O1 + OMH = 90 độ (2 góc nhọn phụ nhau)

O2 + OMK = 90 độ (2 góc nhọn phụ nhau)

Ta lại có: O1 = O2 (vì Oz là tia phân giác của góc xOy)

=> OMH = OMK

Xét 2 tam giác OMH và tam giác OMK ta có:

• OMH = OMK

• OM là cạnh chung

• OHM = OKM

Vậy OMH = OMK (g.c.g)

Dạng 2 - Sử dụng trường hợp bằng nhau của tam giác để chứng minh 1 tính chất khác

Phương pháp giải:

• Đầu tiên chọn 2 tam giác có cạnh hoặc góc là 2 đoạn thẳng hoặc góc cần chứng minh bằng nhau.

• Chứng minh 2 tam giác ấy bằng nhau theo các trường hợp bằng nhau của hai tam giác. Sau đó suy ra 2 cạnh hoặc góc tương ứng bằng nhau và kiểm tra 3 điều kiện bằng nhau.

• Cuối cùng kết hợp các tính chất đã học về tia phân giác, đường thẳng song song, đường trung trực, tổng 3 góc trong 1 tam giác,... để chứng minh 1 tính chất khác.

Bài tập vận dụng

Cho xOy, với Oz là tia phân giác của góc đó. Gọi I là 1 điểm trên tia Oz (I khác O). Kẻ IM vuông góc với Ox (M Ox), IN vuông góc với Oy (N Oy). Biết độ dài đoạn thẳng IM là 2 cm, tính độ dài đoạn thẳng IN?

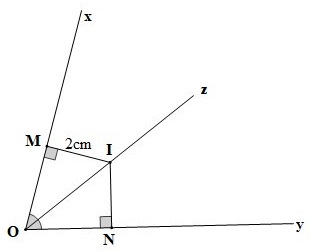
Cách giải:

Xét 2 tam giác OIM và OIN ta có:

• OMI = ONI = 90 độ

• IOM = ION (do Oz là tia phân giác của xOy)

• OI là cạnh chung

Do đó OMI = ONI (cạnh huyền - góc nhọn)

=> IM = IN (2 cạnh tương ứng)

Mà IM = 2cm (giả thiết) => IN = 2cm

Kết luận độ dài đoạn thẳng IN là 2cm.

Bài tập tự luyện

Bài tập 1: Cho tam giác ABC với M là trung điểm BC, N là 1 điểm trong tam giác sao cho NB = NC. Chứng minh tam giác NMB bằng tam giác NMC.

Bài tập 2: Cho tam giác ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Hãy chứng minh rằng tam giác ABE bằng tam giác ACE.

Bài tập 3: Cho tam giác ABC có A = 40 độ, AB = AC. Gọi M là trung điểm của BC. Hãy tính các góc của tam giác AMB và tam giác AMC.

Bài tập 4: Cho tam giác ABC có AB = AC với các điểm D, E thuộc cạnh BC sao cho BD = DE = EC, biết AD = AE.

1. Chứng minh EAB = DAC

2. Gọi M là trung điểm của BC, chứng minh AM là phân giác của góc DAE

3. Giả sử DAE = 60 độ. Tính các góc còn lại của tam giác DAE.

Trên đây, thayphut.net đã tổng hợp các trường hợp bằng nhau của hai tam giác và các dạng bài tập thường gặp kèm phương pháp giải. Các em có thể tham khảo thêm các bài tập vận dụng để hiểu bài và thực hành ngay cùng các bài tập tự luyện.