Quan hệ giữa góc và cạnh đối diện, lý thuyết và bài tập

Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác. Tìm hiểu 2 dạng toán thường gặp và cách vận dụng lý thuyết để giải bài tập.

Quan hệ giữa góc và cạnh đối diện trong tam giác là kiến thức trong chương trình Toán 7 mà các em cần nắm. Bài viết sau đây thayphu sẽ tổng hợp các nội dung về lý thuyết, phương pháp giải các dạng bài tập cùng ví dụ minh họa chi tiết, dễ hiểu nhất!

Lý thuyết về quan hệ giữa góc và cạnh đối diện

quan he giua goc va canh doi dien 1 jpg

Tìm hiểu về quan hệ giữa góc và cạnh đối diện trong tam giác

Góc đối diện với cạnh lớn hơn trong 1 tam giác

Định lý 1: Trong 1 tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

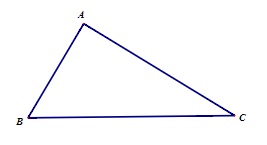
quan he giua goc va canh doi dien 2 jpg

Ví dụ: Cho ABC (AC > AB), khi đó:

Cạnh AB là cạnh đối diện với góc C
Cạnh AC là cạnh đối diện với góc B

AC > AB => B > C

Cạnh đối diện với góc lớn hơn trong 1 tam giác

Định lý 2: Trong 1 tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Ví dụ: Trong ABC có:

Góc C là góc đối diện với cạnh AB
Góc B là góc đối diện với cạnh AC

B > C => AC > AB

Chú ý:

Đối diện với cạnh là góc mà đối diện với góc là cạnh
Trong tam giác tù hoặc tam giác vuông thì góc tù và góc vuông là góc lớn nhất nên cạnh đối diện với góc vuông (cạnh huyền), cạnh đối diện với góc tù là cạnh lớn nhất.
Định lý 1 và 2 chỉ đúng khi ta áp dụng trong 1 tam giác.
Trong tam giác cạnh nhỏ nhất đối diện với góc nhọn.

Các dạng bài về quan hệ giữa góc và cạnh đối diện

Sau khi tìm hiểu về lý thuyết, chúng ta sẽ cùng xem có bao nhiêu dạng bài tập liên quan đến góc và cạnh đối diện trong tam giác:

quan he giua goc va canh doi dien 3 jpg

Các dạng bài tập liên quan đến góc và cạnh trong một tam giác

Dạng 1 - So sánh các góc trong một tam giác

Phương pháp giải:

Trường hợp 1: Nếu các góc cần so sánh nằm trong cùng 1 tam giác thì ta áp dụng định lí 1: “So sánh các cạnh đối diện với các góc đó”.
Trường hợp 2: Nếu các góc cần so sánh không cùng nằm trong 1 tam giác thì ta dùng góc trung gian để so sánh.

Bài tập 1

Cho tam giác ABC có 3 góc nhọn, AB < AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. So sánh góc DBC và ECB.

Lời giải:

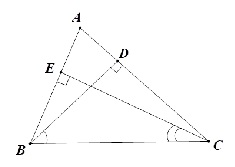
quan he giua goc va canh doi dien 4 jpg

Xét ABC có AB < AC => ACB < ABC (quan hệ giữa cạnh và góc trong tam giác)

DBC có DBC = 90 độ - ACB (1) (trong tam giác vuông 2 góc nhọn phụ nhau)

ECB có ECB = 90 độ - ABC (2) (trong tam giác vuông 2 góc nhọn phụ nhau)

Ta lại có: ACB < ABC (giả thiết) (3)

Từ (1) (2) (3) => DBC > ECB

Bài tập 2

Cho tam giác ABC có AB < AC, gọi M là trung điểm của BC. Hãy chứng minh MAB > MAC

Lời giải:

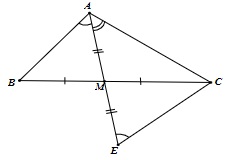
quan he giua goc va canh doi dien 5 jpg

Trên tia đối của tia MA lấy điểm E sao cho AM = ME

ABM = ECM (c.g.c)

=> AB = EC (2 cạnh tương ứng)

=> BAM = CEM (2 góc tương ứng) (1)

Xét AEC có CE < AC (vì EC = AB < AC)

=> EAC < AEC (quan hệ giữa góc và cạnh đối diện trong tam giác) (2)

Từ (1) và (2) => MAB > MAC (đpcm)

Bài tập 3

Cho ABC đều, trên cạnh BC lấy điểm M sao cho BM = ⅓ BC. Chứng minh rằng BAM < 20 độ.

Lời giải:

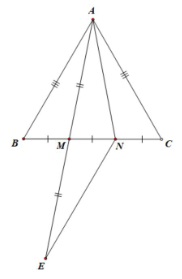
quan he giua goc va canh doi dien 6 jpg

Gọi N là điểm trên BC sao cho BM = MN = NC

ABC đều nên BAC = ABC = ACB = 60 độ

ABM = ACN (c.g.c)

=> BAM = CAN (2 góc tương ứng)

Trên tia đối của tia MA lấy điểm E sao cho AM = ME

ABM = ENM (c.g.c)

=> AB = EN (2 cạnh tương ứng)

ABM có B = 60 độ, BAM < 30 độ

(Vì ABC đều BM = ⅓ BC => BM < BC/2 nên BAM < 30 độ)

=> AMB > 90 độ

=> ABM < AMB => AM < AB (quan hệ giữa cạnh và góc trong tam giác)

EN > AM mà AM = AN (ABM = ACN)

=> EN > AN hay EAN > AEN => MAN > BAM

Mà BAM + MAN + NAC = 60 độ => MAN + 2BAM = 60 độ

Mặt khác MAN > BAM => 3 BAM < 60 độ => BAM < 20 độ (đpcm)