Sự đồng quy của 3 đường trung trực, lý thuyết và các bài tập

Lý thuyết và các dạng toán thường gặp về sự đồng quy của 3 đường trung trực kèm phương pháp giải chi tiết. Qua đây các em có thể vận dụng giải bài tập hiệu quả.

Sự đồng quy của 3 đường trung trực là một nội dung các em sẽ được học trong chương trình Toán lớp 7. Bài viết sau đây thayphu sẽ tổng hợp lại các kiến thức lý thuyết và bài tập giúp các em ôn luyện dễ dàng, hãy cùng theo dõi nhé!

Đường trung trực của tam giác

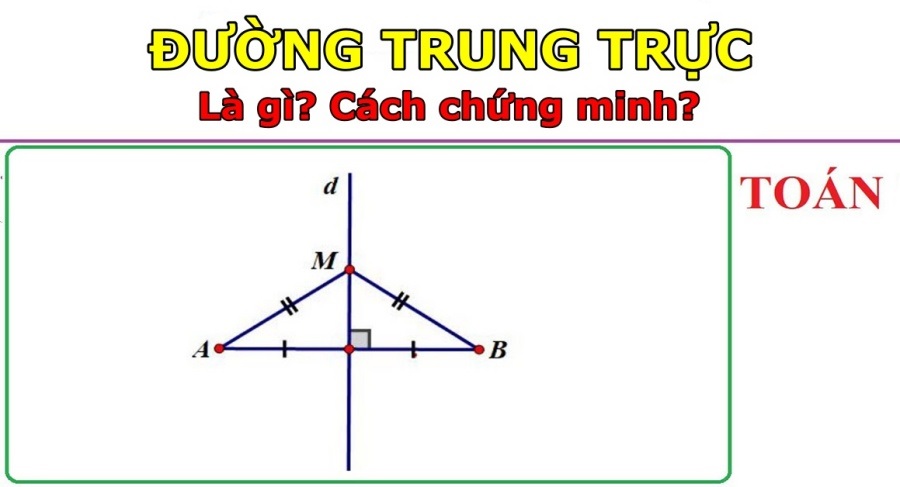
Lý thuyết về đường trung trực trong tam giác

Định nghĩa: Xét trong một tam giác, đường trung trực của các cạnh chính là đường trung trực của tam giác.

Định lý 1: Ba đường trung trực của tam giác đồng quy tại 1 điểm và điểm đó cách đều 3 đỉnh của tam giác.

Nhận xét: Vì giao điểm của ba đường trung trực của tam giác cách đều 3 đỉnh của tam giác nên là tâm đường tròn đi qua 3 đỉnh tam giác đó.

Tính chất: Tam giác ABC cân tại A, AM là đường trung tuyến thì nó cũng là đường trung trực của BC.

Cụ thể:

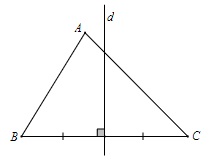
1. Cho tam giác ABC (d) là đường trung trực của cạnh BC thì (d) gọi là đường trung trực của tam giác ABC ứng với cạnh BC.

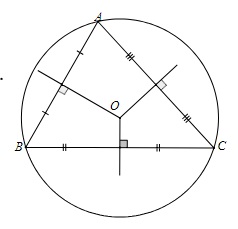
2. Trong hình dưới đây, điểm O là giao điểm các đường trung trực của tam giác ABC. Ta có: OA = OB = OC và điểm O là tâm đường tròn ngoại tiếp của ABC.

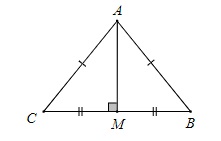
3. Xét ABC cân tại A có AM là đường trung tuyến và chính là đường trung trực của cạnh BC.

Đường cao của tam giác

Định nghĩa: Đoạn thẳng kẻ từ 1 đỉnh tam giác và vuông góc với cạnh đối diện thì được gọi là đường cao của tam giác.

Định lý 2: Ba đường cao của tam giác đồng quy tại một điểm và điểm đó gọi là trực tâm của tam giác.

Cụ thể:

1. AH là một đường cao của tam giác ABC ⇔ AH vuông góc BC

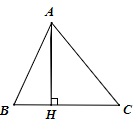
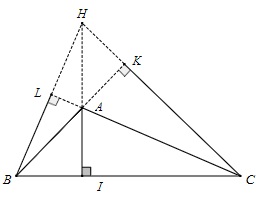
2. Xét hình vẽ dưới đây có AD, BE, CF là các đường cao, H là trực tâm của tam giác ABC.

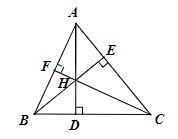
Chú ý:

• Tam giác ABC là tam giác nhọn thì H nằm trong tam giác

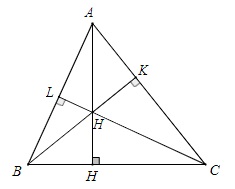
• Tam giác ABC là tam giác vuông tại A thì điểm H trùng với điểm A

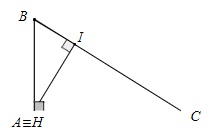
• Tam giác ABC là tam giác tù thì điểm H nằm ngoài tam giác

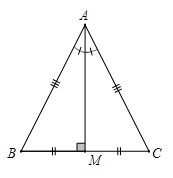
Tính chất trong tam giác cân: Tam giác ABC cân tại A, AM là đường cao và cũng chính là đường trung trực, đường trung tuyến, đường phân giác.

Các dạng bài về sự đồng quy của 3 đường trung trực

Sau đây là 3 dạng toán thường gặp liên quan đến sự đồng quy của 3 đường trung trực và phương pháp giải:

Các dạng bài tập về sự đồng quy của 3 đường trung trực

Dạng 1 - Bài tập tâm đường tròn ngoại tiếp của tam giác

Phương pháp giải:

• Dựa vào lý thuyết về sự đồng quy của 3 đường trung trực trong tam giác
• Sử dụng tính chất giao điểm các đường trung trực trong tam giác thì cách đều 3 đỉnh của tam giác đó.

Bài tập 1

Cho A, B, C là 3 điểm phân biệt không thẳng hàng. Xác định đường tròn đi qua 3 điểm đó.

Lời giải:

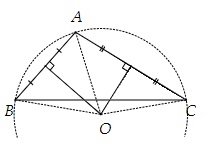
Gọi đường tròn đi qua 3 điểm A, B, C có tâm O ta có: OA = OB = OC

Bên cạnh đó, 3 điểm phân biệt A, B, C không thẳng hàng tạo thành ABC.

Vì OA = OB = OC nên O là giao điểm 3 đường trung trực của tam giác ABC.

Vậy đường tròn đi qua 3 điểm A, B, C có tâm O là giao của 3 đường trung trực của tam giác ABC và bán kính bằng OA.

Bài tập 2

Cho tam giác ABC với A > 90 độ và các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E. Nối AD, AE, OB, OC. Hãy tìm tam giác nào bằng với OAD và OAE.

Lời giải:

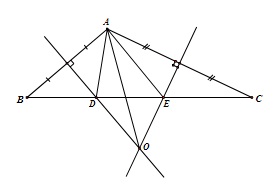
OD là đường trung trực của AB

Suy ra DA = DB, OA = OB

Do đó tam giác OAD = tam giác OBD (c.c.c)

Tương tự tam giác OAE = tam giác OCE (c.c.c)

Dạng 2 - Hãy chứng minh 3 đường thẳng đồng quy, 3 điểm thẳng hàng

Phương pháp giải: Dựa vào định lý, tính chất về đường trung trực và sự đồng quy của ba đường trung trực trong tam giác.

Bài tập 1

Cho tam giác ABC cân tại A. Gọi M là trung điểm của BC, với các đường trung trực của AB và AC cắt nhau ở E. Hãy chứng minh ba điểm A, E, M thẳng hàng.

Lời giải:

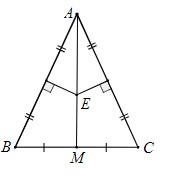
Ta có M là trung điểm của BC (theo giả thiết)

Từ đó suy ra AM là đường trung tuyến của tam giác cân ABC

Ngoài ra AM cũng là đường trung trực của BC (1)

Xét tam giác ABC cân tại A có đường trung trực của AB và AC cắt nhau ở E.

=> E thuộc đường trung trực của BC (theo tính chất 3 đường trung trực của tam giác) (2)

Từ (1) và (2) suy ra, 3 điểm A, E, M thẳng hàng.

Bài tập 2

Cho tam giác ABC cân tại A. Gọi G là trọng tâm, O là giao điểm 3 đường trung trực của tam giác ABC.

1. Tam giác BOC là tam giác gì?
2. Hãy chứng minh rằng A, O, G thẳng hàng

Lời giải

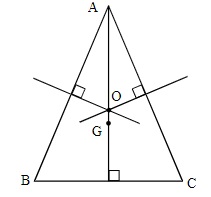
1. Do O là giao điểm 3 đường trung trực của tam giác ABC nên ta có:

OA = OB = OC => BOC chính là tam giác cân tại O

2. Do O là giao điểm 3 đường trung trực của tam giác ABC nên O thuộc đường trung trực của BC (1)

Vì điểm G là trọng tâm => G cũng đường trung tuyến của BC đi qua A (2)

Cùng với đó ABC cân tại A => Trung tuyến ứng với cạnh BC là đường trung trực của BC.

Như vậy G thuộc đường trung trực của BC (3)

Từ (1) (2) và (3) suy ra 3 điểm A, O, G thẳng hàng.

Dạng 3 - Sử dụng tính chất 3 đường trung trực giải các bài toán khác

Phương pháp giải: Dựa vào tính chất về đường trung trực và sự đồng quy của ba đường trung trực trong tam giác.

• Điểm M nằm trên đường trung trực của một đoạn thẳng thì cách đều 2 đầu mút của đoạn thẳng đó.
• ABC cân tại A có AM là đường trung tuyến và là đường trung trực của BC.

Bài tập 1

Cho ABC cân tại A, đường trung tuyến AM và đường trung trực của AC cắt đường thẳng AM tại D. Hãy chứng minh rằng DA = DB.

Lời giải:

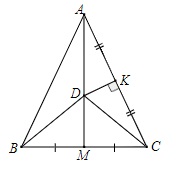
Cách 1:

Ta có tam giác ABC cân ở A nên trung tuyến AM cũng là đường trung trực của BC

Vì D thuộc đường trung trực của AC nên DA = DC (1)

Vì D thuộc đường trung trực của BC nên DB = DC (2)

Từ (1) (2) suy ra DA = DB

Cách 2:

Tam giác ABC cân tại A có AM là đường trung tuyến của cạnh đáy BC nên AM cũng là đường trung trực của BC

Ngoài ra đường trung trực của AC cắt AM tại điểm D

=> D là giao điểm của 2 đường trung trực của cạnh BC và AC suy ra D thuộc đường trung trực của AB

Vì vậy DA = DB

Bài tập 2

Cho cân ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Hãy chứng minh rằng AOB = AOC .

Lời giải:

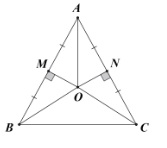
Vì điểm O là giao điểm các đường trung trực của tam giác ABC nên O thuộc đường trung trực của BC.

Tam giác ABC cân tại A => AB = AC

=> A thuộc đường trung trực của BC

Do đó AO là đường trung trực của BC

Tam giác ABC cân tại A nên đường trung trực của AO đồng thời là đường phân giác của A.

Xét tam giác AOB và tam giác AOC có:

• OA là cạnh chung
• AB = AC (tam giác ABC cân tại A)
• OAB = OAC (AO là tia phân giác của góc BAC)

Do đó tam giác AOB = tam giác AOC (c.g.c)

=> AOB = AOC (2 góc tương ứng)

Bài viết vừa gửi đến các em kiến thức cơ bản về sự đồng quy của 3 đường trung trực và các dạng toán thường gặp. Hãy cùng ôn tập, thực hành với các bài tập để hiểu rõ và hoàn thành tốt nội dung này nhé!