Sự đồng quy của 3 đường trung tuyến, lý thuyết và bài tập chọn lọc

Lý thuyết về sự đồng quy của 3 đường trung tuyến là nội dung các em cần nắm trong chương trình Toán 7. Có các dạng toán cơ bản nào và phương pháp giải ra sao?

Sự đồng quy của 3 đường trung tuyến có ý nghĩa trong việc xác định 1 điểm trên các đường này. Để giúp các em ôn tập kiến thức và làm tốt các bài tập, thayphu sẽ tổng hợp đầy các nội dung qua bài viết sau đây, hãy cùng xem chi tiết!

Lý thuyết sự đồng quy của 3 đường trung tuyến

Đường trung tuyến của một tam giác

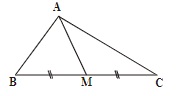
Xét tam giác ABC có đoạn thẳng AM nối đỉnh A của tam giác với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC).

Đoạn thẳng AM cũng được gọi là đường trung tuyến của tam giác ABC và tương tự như vậy thì mỗi tam giác sẽ có 3 đường trung tuyến.

Tính chất về sự đồng quy của 3 đường trung tuyến

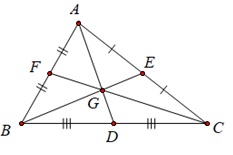
Khi 3 đường trung tuyến của 1 tam giác cùng đi qua 1 điểm hay đồng quy tại 1 điểm. Và điểm gặp nhau của 3 đường trung tuyến được gọi là trọng tâm của tam giác đó.

Vị trí trọng tâm của 1 tam giác cách mỗi đỉnh 1 khoảng bằng ⅔ độ dài đường trung tuyến đi qua đỉnh ấy là AG/AD = BG/BE = CG/CF = ⅔.

Các dạng bài về sự đồng quy của 3 đường trung tuyến

Sau khi tìm hiểu về lý thuyết và tính chất cơ bản, các em hãy cùng xem ngay 3 dạng bài liên quan và phương pháp giải sau đây:

Dạng 1 - Bài tập ứng dụng tính chất trọng tâm của tam giác

Phương pháp giải: Chúng ta có thể vận dụng linh hoạt các tỉ số liên quan đến trọng tâm của tam giác.

Bài tập 1

Cho tam giác ABC có cạnh BC = a, CA = b, AB = c kẻ đường trung tuyến AM và cho AM = ma. Hãy chứng minh rằng: (b + c - a)/2 < ma < (b + c)/2.

Lời giải:

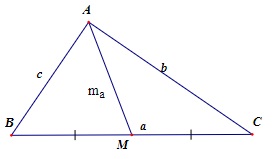
Xét tam giác AMB ta có: AM + MB > AB (1)

Tương tự tam giác AMC ta có: AM + MC > AC (2)

Cộng từng vế (1) và (2) chúng ta sẽ được 2AM + (MB + MC) > AB + AC

Hay là 2ma + a > b + c suy ra ma > (b + c - a)/2

Thực hiện các bước chứng minh tương tự ta có ma < (b+c)/2

Khi đó chúng ta được kết quả là (b + c - a)/2 < ma < (b + c)/2

Bài tập 2

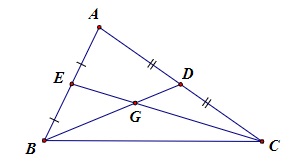
Cho tam giác ABC có 2 đường trung tuyến là BD và CE

1. Hãy tính các tỉ số BG/BD và CG/CE
2. Hãy chứng minh rằng BD + CE > 3/2 BC

Lời giải:

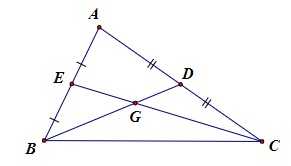
Cho điểm G là giao điểm của 2 đường trung tuyến BD và CE

Xét tam giác GBC ta có: GB + GC > BC (theo bất đẳng thức tam giác)

Bên cạnh đó GB = ⅔ BD và GC = ⅔ CE nên suy ra ⅔ BD + ⅔ CE > BC.

Từ đó kết luận BD + CE > 3/2 BC.

Bài tập 3

Cho tam giác ABC có cạnh BC = 8cm, các đường trung tuyến BD, CE cắt nhau tại điểm G. Hãy chứng minh rằng tổng BD + CE > 12cm.

Lời giải:

Xét tam giác GBC ta có: GB + GC > BC (theo bất đẳng thức tam giác)

Bên cạnh đó GB = ⅔ BD, GC = ⅔ CE nên suy ra ⅔ BD + ⅔ CE > BC

Kết quả là BD + CE > 3/2 BC = 3/2.8 = 12

Dạng 2 - Chứng minh 1 điểm là trọng tâm của tam giác

Phương pháp giải: Để chứng minh được 1 điểm là trọng tâm của tam giác ta áp dụng 2 cách như sau:

• Cách 1: Chứng minh rằng điểm đó là giao điểm của 2 đường trung tuyến trong tam giác
• Cách 2: hứng minh rằng điểm đó thuộc đường trung tuyến của tam giác và thỏa mãn được 1 trong số các tỉ lệ về tính chất trọng tâm của tam giác.

Bài tập 1

Cho 2 đường thẳng xx’ và yy’ cùng cắt nhau ở điểm O. Trên tia Ox ta lấy 2 điểm A và B sao cho điểm A nằm giữa O và B, AB = 2OA. Trên tia yy’ lấy 2 điểm L, M sao cho điểm O trở thành trung điểm của LB. Hãy chứng minh rằng đoạn thẳng LP, MQ cùng đi qua A.

Lời giải:

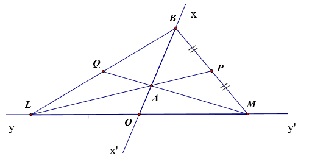
Theo bài ra ta có điểm O là trung điểm của đoạn LM

=> BO là đường trung tuyến của tam giác BLM (1)

Bên cạnh đó: BO = BA + AO vì điểm A nằm giữa O và B hay OB = 2OA + OA = 3OA.

Từ đó ta được BA = ⅔ BO (2)

Từ (1) (2) suy ra điểm A là trọng tâm của tam giác BLM

Cùng với LP, MQ là các đường trung tuyến của tam giác BLM. Bởi vì điểm P là trung điểm của MB và điểm O là trung điểm của đoạn LM.

Như vậy các đoạn thẳng LP và MQ cùng đi qua A (tính chất 3 đường trung tuyến)

Bài tập 2

Cho tam giác ABC có đường trung tuyến AD. Trên tia AD ta lấy điểm E sao cho AD = DE, tương tự trên tia BC lấy điểm M sao cho BC = CM. Hãy chứng minh rằng điểm C là trọng tâm của tam giác AEM.

Lời giải:

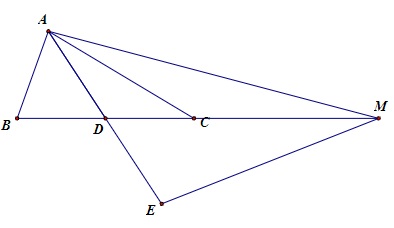
Theo đề ra ta có AD = DE nên điểm C thuộc MD là đường trung tuyến của tam giác AEM (1)

Cùng với đó BC = 2CD và BC = CM nên CM = 2CD (2)

Từ (1) (2) ta kết luận được điểm C là trọng tâm của tam giác AEM.

Bài tập 3

Cho tam giác ABC, trên đường trung tuyến AM ta lấy 2 điểm D và E sao cho AD = DE = EM. Hãy chứng minh rằng điểm E là trọng tâm của tam giác ABC.

Lời giải:

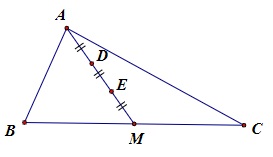
Theo bài ra ta có AD = DE = EM nên AE = 2/3AM

Mà điểm E thuộc trung tuyến AM nên điểm E chính là trọng tâm của tam giác ABC.

Dạng 3 - Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều

Phương pháp giải: Áp dụng các tính chất liên quan của tam giác vuông, tam giác cân, tam giác đều.

Bài tập 1

Cho tam giác ABC cân tại điểm A có trung tuyến AM. Hãy chứng minh AM vuông góc với BC.

Lời giải:

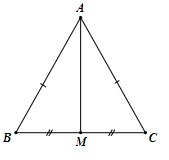
Tiến hành xét 2 ABM và ACM ta có:

AB = AC (giả thiết)

BM = CM (giả thiết)

AM là cạnh chung

Suy ra ABM = ACM (c.c.c) nên AMB = AMC (2 góc tương ứng)

Mà AMB + AMC = 180 độ nên AMB = AMC = 90 độ hay AM BC.

Bài tập 2

Cho tam giác ABC có các đường trung tuyến là BD và CE bằng nhau. Hãy chứng minh tam giác ABC cân.

Lời giải:

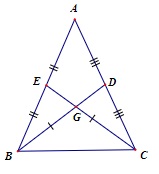
Gọi điểm G là giao điểm của BD và CE ta được:

BG = ⅔ BD, CG = ⅔ CE

Vì BD = CE nên BG = CG. GD = GE => BGE = CGD (c.g.c) => BE = CD

Cùng với đó: BE = ½ AB, CD = ½ CA

Suy ra AB = AC nên kết luận ABC cân tại A.

Bài tập 3

Cho tam giác ABC có đường trung tuyến AM và K là trung điểm của BM. Trên tia đối của tia KA lấy điểm E sao cho KE = KA.

1. Điểm M là trọng tâm của tam giác nào? Vì sao?
2. Gọi điểm F là trung điểm của CE, hãy chứng minh 3 điểm A, M, F thẳng hàng

Lời giải:

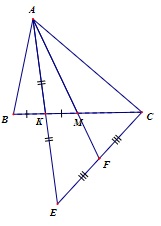
Xét tam giác ACE có KA = KE (theo bài ra) => CK là đường trung tuyến

Ta lại có CM = 2/3CK nên điểm M là trọng tâm của tam giác ACE.

Do điểm F là điểm của EC (theo bài ra) nên AF là đường trung tuyến thứ 3 của tam giác ACE.

Mà điểm M là trọng tâm nên AF đi qua điểm M hay 3 điểm A, M, F thẳng hàng.

Trên đây là tổng hợp lý thuyết và 3 dạng toán cơ bản về sự đồng quy của 3 đường trung tuyến. Các em nắm chắc phương pháp giải chi tiết và thực hành với các bài tập cụ thể để hiểu bài nhé!