Tổng góc trong của tam giác, lý thuyết và các dạng bài tập

Tổng góc trong của tam giác là phần kiến thức cơ bản trong chương trình Toán 7. Cùng tham khảo ngay các dạng bài tập và phương pháp giải chi tiết.

Tổng góc trong của tam giác sẽ bằng 180 độ. Bài viết sau đây thayphu sẽ giúp các em ôn tập lại các lý thuyết và tập hợp các toán cơ bản liên quan. Đây sẽ là nguồn tài liệu để các em củng cố kiến thức và chuẩn bị tốt nhất cho kỳ thi sắp tới!

Lý thuyết về tổng các góc trong một tam giác

Tổng góc trong của tam giác là tổng số đo 3 góc trong tam giác đó.

Tổng 3 góc trong của 1 tam giác bằng 180 độ.

Góc ngoài của tam giác là góc kề bù với 1 góc của tam giác.

Mỗi góc ngoài của 1 tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.

Ví dụ minh họa:

Cho tam giác ABC có các góc A2, góc B, góc C là các góc trong của tam giác.

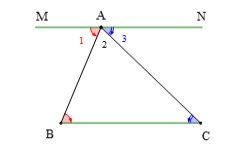
Qua điểm A kẻ đường thẳng MN // BC, ta có:

B = A1 (2 góc so le trong)

C = A3 (2 góc so le trong)

Mà A1 + A2 + A3 = 180 độ => B + A2 + C = 180 độ

Vậy nên tổng 3 góc trong tam giác ABC bằng 180 độ.

Chú ý:

• Tam giác có 3 góc đều nhọn được gọi là tam giác nhọn.
• Tam giác có 1 góc tù được gọi là tam giác tù.
• Tam giác có 1 góc vuông được gọi là tam giác vuông. Trong tam giác vuông, 2 cạnh của góc vuông được gọi là cạnh góc vuông. Cạnh còn lại được gọi là cạnh huyền.
• 2 góc có tổng số đo bằng 90 độ được gọi là 2 góc phụ nhau. Trong tam giác vuông 2 góc nhọn phụ nhau.

Mẹo ghi nhớ tổng góc trong của tam giác

Với một tam giác bất kỳ, tổng số đo các góc đều sẽ bằng 180 độ.

Định lý này đã được thừa nhân, trong đó công thức tính tổng số đo các góc trong của 1 đa giác như sau: Tổng số đo = (n - 2).180 với n là số cạnh của đa giác.

• Trong tam giác vuông, tổng số đo 2 góc phụ nhau bằng 90 độ.

Áp dụng định lý về tổng ba góc trong 1 tam giác vào tam giác vuông thì tam giác vuông có 1 góc bằng 90. Nên 2 góc còn lại sẽ bằng 180 độ - 90 độ = 90 độ. Bởi vậy ta nói 2 góc nhọn của tam giác phụ nhau.

• Các góc ngoài của tam giác bằng tổng số đo của 2 góc không kề với nó

Vì góc ngoài của tam giác và góc trong kề với nó có tổng bằng 180 độ. Trong khi tổng 3 góc trong của tam giác bằng 180 độ. Vì vậy số đo góc ngoài của tam giác bằng tổng số đo của 2 góc trong không kề với nó.

• Góc ngoài của tam giác luôn có số đo lớn hơn mỗi góc trong không kề với nó

Ta thấy góc ngoài của tam giác bằng tổng số đo các góc trong không kề với nó. Vì vậy góc ngoài luôn luôn lớn hơn mỗi góc trong.

Góc ngoài của tam giác

Góc ngoài của tam giác là góc kề bù với một góc của tam giác.

Tính chất:

• Mỗi góc ngoài của tam giác sẽ bằng tổng của 2 góc trong không kề với nó.
• Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.

Các dạng toán về tổng góc trong của tam giác thường gặp

Dạng 1 - Tính số đo góc của 1 tam giác

Phương pháp giải:

Lập các đẳng thức thể hiện tổng 3 góc của 1 tam giác bằng 180 độ. Trong tam giác vuông 2 góc nhọn phụ nhau. Góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó. Từ đó sẽ tính được số đo góc cần tìm.

Bài tập vận dụng:

Tính số đo x trong các hình dưới đây:

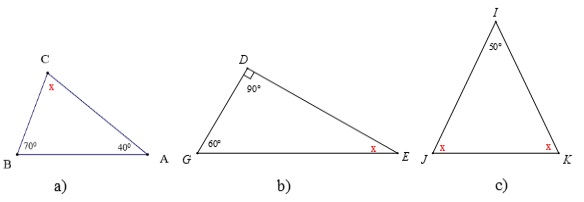
Cách giải:

1. Xét tam giác ABC có: A + B + C = 180 độ (tổng 3 góc trong tam giác)

Do đó: 40 độ + 70 độ + x = 180 độ

=> x = 180 độ - 40 độ - 70 độ => x = 70 độ

Vậy góc x = 70 độ.

2. Xét tam giác DGE có: D + G + E = 180 độ (tổng 3 góc trong tam giác)

Do đó: 90 độ + 60 độ + x = 180 độ

=> x = 180 độ - 90 độ - 60 độ => x = 30 độ

Kết luận góc x = 30 độ.

3. Xét tam giác IJK có: I + J + K = 180 độ (tổng 3 góc trong tam giác)

Do đó: 50 độ + x + x =180 độ

=> x + x = 180 độ - 50 độ => 2x = 130 độ => x = 65 độ

Kết luận góc x = 65 độ.

Dạng 2 - Nhận biết tam giác vuông

Phương pháp giải:

Dấu hiệu nhận biết tam giác vuông là chỉ ra trong tam giác đó có 1 góc bằng 90 độ. Trong tam giác vuông thì 2 góc nhọn phụ nhau.

Bài tập vận dụng

Cho các tam giác sau đây, hãy cho biết tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?

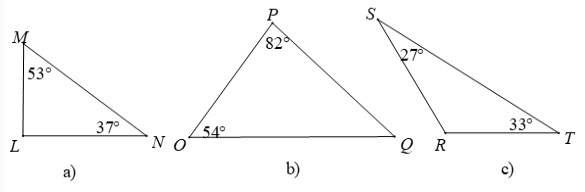
Cách giải:

1. Xét tam giác MLN có: M + L + N = 180 độ (tổng 3 góc trong tam giác)

Do đó: 53 độ + L + 37 độ = 180 độ

=> L = 180 độ - 53 độ - 37 độ = 90 độ

Vì L là góc vuông nên tam giác MLN là tam giác vuông.

2. Xét tam giác POQ có: P + O + Q = 180 độ (tổng 3 góc trong tam giác)

Do đó: 82 độ + 54 độ + Q = 180 độ

=> Q = 180 độ - 82 độ - 54 độ = 44 độ < 90 độ

=> P, O, Q là góc nhọn nên tam giác POQ là tam giác nhọn.

3. Xét tam giác SRT có: S + R + T = 180 độ (tổng 3 góc trong tam giác)

Do đó: 27 độ + R + 33 độ = 180 độ

=> R = 180 độ - 27 độ - 33 độ = 120 độ > 90 độ.

=> R là góc tù nên tam giác SRT là tam giác tù.

Dạng 3: So sánh các góc dựa vào tính chất góc ngoài của tam giác

Phương pháp giải: Sử dụng tính chất góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.

Bài tập vận dụng

Cho tam giác ABC có A = 80 độ, 2 tia phân giác BD và CE cắt nhau tại điểm I.

1. Tính góc BIC
2. So sánh các góc BIC, BDC và BAC

Cách giải:

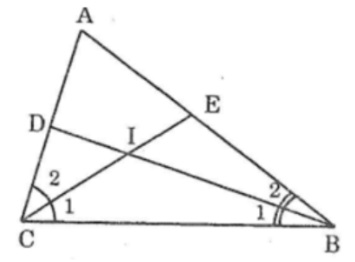
1. Ứng dụng định lý tổng 3 góc trong tam giác ta có:

A + ABC + ACB = 180 độ

=> ABC + ACB = 180 độ - A

=> ABC + ACB = 180 độ - 80 độ = 100 độ

=> B1 + C1 = (ABC + ACB) / 2 = 100 độ / 2 = 50 độ (vì BD, CE là tia phân giác)

Tương tự xét tam giác BIC ta có:

BIC + B1 + C1 = 180 độ

BIC = 180 độ - (B1 + C1) = 180 độ - 50 độ = 130 độ

Vậy BIC =130 độ.

2. Ta có BIC là góc ngoài ứng với đỉnh I của tam giác IDC

=> BIC > IDC hay BIC > BDC (1)

Tương tự xét tam giác ADB, BDC > BAC (2)

Từ (1) và (2) suy ra BIC > BDC > BAC.

Bài tập tự luyện

Bài tập 1: Trong tam giác vuông ABC có số đo một góc bằng 36 độ. Vậy số đo góc nhọn còn lại là bao nhiêu?

1. 64 độ
2. 54 độ
3. 44 độ
4. 74 độ

Bài tập 2: Trong tam giác ABC có A = 70 độ, B - C = 50 độ. Số đo của góc C sẽ là bao nhiêu?

1. 80 độ
2. 60 độ
3. 30 độ
4. 40 độ

Bài tập 3: Cho tam giác ABC có A = 50 độ, B = 70 độ. Tia phân giác của góc C cắt AB tại điểm M. Hãy tính AMC, BMC.

Bài tập 4: Tam giác ABC có B + C = A; C = 2B. Tia phân giác của góc C cắt AB tại điểm D. Hãy tính ADC, BDC.

Bài tập 5: Cho tam giác ABC có A = 90 độ. Gọi d là đường thẳng đi qua C và vuông góc với BC. Tia phân giác của góc B cắt AC ở điểm D và cắt d ở điểm E. Kẻ CH vuông góc DE (H DE). Hãy chứng minh rằng CH là phân giác của DCE.

Bài viết vừa tổng hợp lại phần lý thuyết về tổng góc trong của tam giác, các dạng toán liên quan cùng phương pháp giải chi tiết. Các em có thể tham khảo ngay các bài tập vận dụng có lời giải và thực hành ngay cùng các bài tập tự luyện.