Tính số đo góc toán lớp 7, phương pháp giải và bài tập vận dụng

Phương pháp tính số đo góc lớp 7, sử dụng linh hoạt các tính chất về góc của 1 tam giác, góc ngoài tại 1 đỉnh hay tính chất tia phân giác của góc.

Tính số đo góc lớp 7 là một nội dung cơ bản trong chương trình Toán 7 mà các em cần nắm vững. Bài viết này thayphu sẽ tổng hợp lại các kiến thức lý thuyết quan trọng. Từ đó các em sẽ có thể vận dụng làm tốt các dạng bài tập được giao. Hãy cùng theo dõi ngay sau đây nhé!

Làm sao để tính số đo góc lớp 7?

Nắm vững kiến thức để biết cách tính số đo góc

Phương pháp giải

Để giải các bài toán về tính số đo góc lớp 7 thì chúng ta phải nắm vững các kiến thức cơ bản sau đây:

1. Trong tam giác thường

• Tổng ba góc trong của tam giác bằng 180 độ
• Khi biết 2 góc chúng ta sẽ xác định được góc còn lại.

2. Trong tam giác cân: Biết được 1 góc chúng ta xác định được 2 góc còn lại.

3. Trong tam giác vuông

• Biết 1 góc nhọn, chúng ta xác định được góc nhọn còn lại
• Cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh góc vuông đó có số đo bằng 30 độ.

4. Trong tam giác vuông cân: Mỗi góc nhọn có số đo bằng 45 độ

5. Trong tam giác đều: Mỗi góc có số đo bằng 60 độ

6. Đường phân giác của 1 góc chia góc đó ra 2 góc có số đo bằng nhau

7. Hai đường phân giác của 2 góc kề bù thì vuông góc với nhau

8. Hai góc đối đỉnh thì bằng nhau

9. Tính chất về góc so le trong, đồng vị, trong cùng phía của 1 đường thẳng cắt 2 đường thẳng song song.

Trong thực tế, để giải các bài toán về tính số đo góc lớp 7 chúng ta thường xét các góc đó nằm trong mối liên hệ với các góc ở các hình đặc biệt đã nêu ở trên hoặc xét các góc tương ứng bằng nhau,... rồi suy ra kết quả.

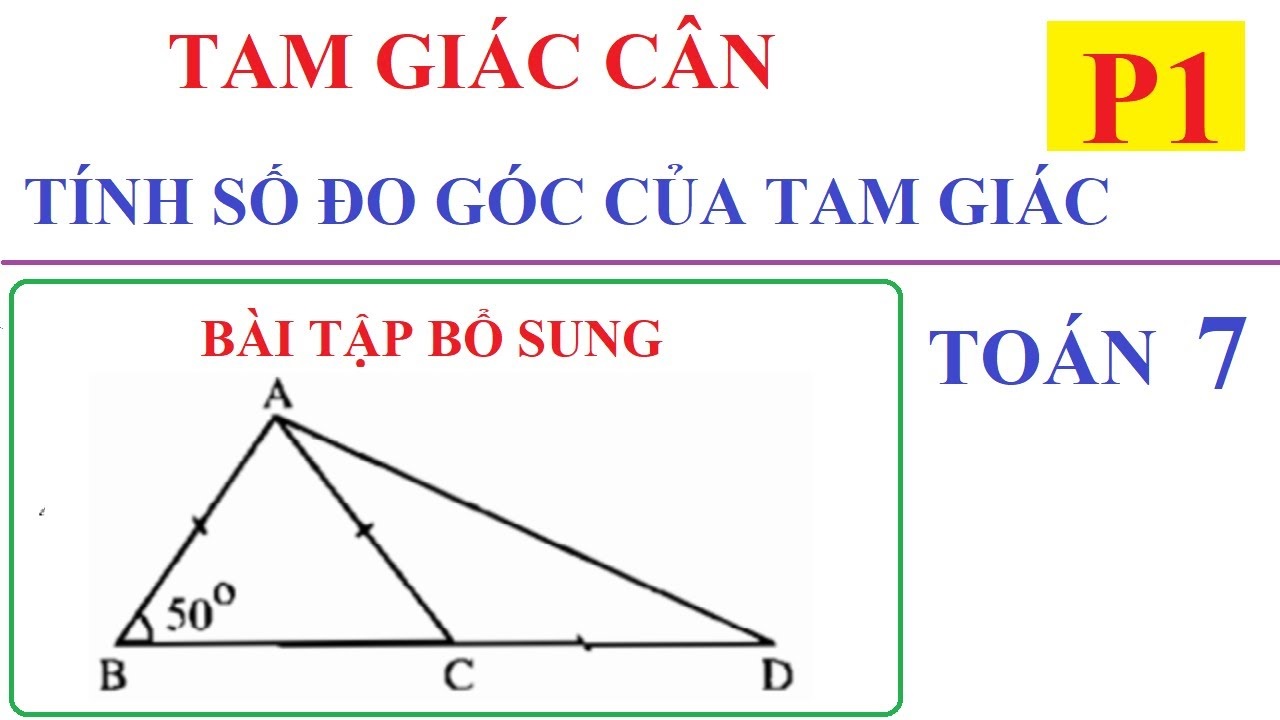Các dạng bài tập tính số đo góc lớp 7

Ví dụ minh họa

Cho tam giác ABC, góc C = 30 độ. Kẻ AH vuông góc với BC tại H biết rằng AH = ½ BC. Gọi D là trung điểm của AB. Tính số đo góc ACD?

Cách giải:

Xuất phát từ tam giác AHC vuông có góc C = 30 độ và AH = ½ BC. Từ 2 yếu tố này chúng ta nghĩ tới tam giác vuông có 1 góc bằng 30 độ. Với lập luận đó, ta có thể chứng minh tam giác ABC cân.

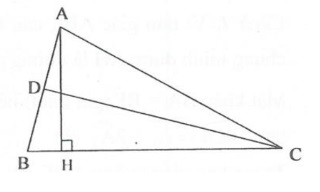
Xét tam giác AHC có: C = 30 độ, AHC = 90 độ

=> AH = ½ AC

Mà AH = ½ BC => AC = BC

=> Tam giác ACB cân tại C => CD là đường phân giác của góc C

=> ACD = 15 độ

Các dạng bài tập liên quan đến tính số đo góc lớp 7

Các em cùng tham khảo các dạng toán liên quan đến tính số đo góc lớp 7, phương pháp giải cùng bài tập chi tiết như sau:

Dạng 1 - Tính số đo của 1 góc, so sánh các góc

Phương pháp giải:

Lập đẳng thức thể hiện tổng ba góc của tam giác bằng 180 độ. Trong tam giác vuông, 2 góc nhọn phụ nhau. Góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó. Sau đó tính số đo góc phải tìm.

Bài tập vận dụng

Bài 1: Cho tam giác ABC có tia giác góc B và góc C cắt nhau tại điểm I. Gọi M là trung điểm của đoạn thẳng BC. Biết rằng BI = 2IM và BIM = 90 độ. Tính số đo góc A?

Cách giải:

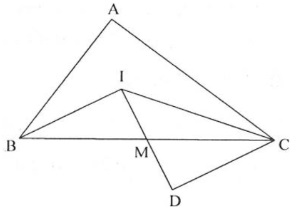
Trên tia đối của tia MI lấy MD = MI, BMI = CMD, IM = DM

Suy ra BIM = CDM (c.g.c)

=> BI = CD, BIM = CDM => CDI = 90 độ

Từ BI = 2IM => BI = ID = 2IM

=> CD = ID => CDI vuông cân tại D

=> CID = 45 độ => BIC = 135 độ

BIC có BIC = 135 độ nên IBC - ICB = 45 độ

BI, CI là tia phân giác B và C nên ABC + ACB = 2IBC + ICB = 90 độ

Vậy kết luận A = 90 độ.

Bài 2: Cho tam giác ABC cân tại A với BAC < 90 độ và kẻ BD, AH lần lượt vuông góc với AC, BC. Trên tia BD lấy điểm K sao cho BK = BA. Tính số đo HAK.

Cách giải:

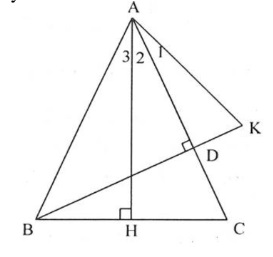
Vì tam giác ABC cân tại A có AH vuông góc với BC nên dễ dàng chứng minh được AH là đường phân giác của BAC suy ra A2 = A3.

Mặt khác: BA = BK (giả thiết) nên ABK cân tại B => BKA = BAK hay BKA = A1 + 2A2 (1)

Trong tam giác vuông ADK có:

K + A1 = 90 độ (2)

Thay (1) vào (2) ta được:

2A1 + 2A2 = 90 độ

Suy ra A1 + A2 = 45 độ

Vậy HAK = 45 độ.

Dạng 2 - Các bài toán chứng minh góc

Phương pháp giải:

Sử dụng linh hoạt các tính chất về góc của 1 tam giác, góc ngoài tại 1 đỉnh hay tính chất tia phân giác của góc.

• B1: Áp dụng tính chất tổng 3 góc trong tam giác, tính góc trong yêu cầu của bài toán.
• B2: Kết hợp tính chất đường phân giác để chứng minh hệ thức.

Bài tập vận dụng

Cho tam giác ABC cân tại A có A = 3B. Trên nửa mặt phẳng bờ BC, chứa điểm A, vẽ tia Cy sao cho BCy = 132 độ. Tia Cy cắt tia phân giác Bx của B tại D. Tính số đo góc ADB.

Cách giải:

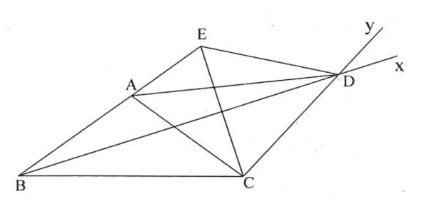
Từ giả thiết ABC cân tại A và A = 3B, suy ra B = C = 36 độ. Trên tia BA lấy điểm E sao cho BE = BC (E nằm ngoài đoạn AB). Khi đó Bx là tia phân giác của ABC. Từ đó dễ dàng chứng minh được BD vuông góc với CE.

EBC cân tại B có EAC = ABC + ACB = 72 độ

=> AEC = (180 độ - 36 độ) /2 = 72 độ

Do đó AEC = CAE => ACE cân tại C nên CA = CE (1)

Ta lại có DEC cân tại D và ECD = 132 độ - 72 độ = 60 độ nên DEC là tam giác đều (2)

Từ (1) và (2) suy ra CAD cân tại C, có ACD = 132 độ - 36 độ = 96 độ

=> ADC = (180 độ - 96 độ) / 2 = 42 độ.

Trong BCD có BDC = 180 độ - 132 độ - 18 độ = 30 độ

=> ADB = ADC - BDC = 42 độ - 30 độ = 12 độ

Vậy ADB = 12 độ.

Bài tập tự luyện

Bài 1: Cho tam giác ABC cân tại A, có góc A = 80 độ. Điểm D thuộc miền trong tam giác sao cho góc DBC = 10 độ, góc DCB = 30 độ. Tính số đo góc ADB.

Bài 2: Cho tam giác ABC, biết B = 45 độ, A = 15 độ. Trên tia đối của tia CB lấy điểm D sao cho CD = 2BC. Vẽ DE AC, E thuộc AC.

1. Hãy chứng minh rằng EB = ED
2. Tính số đo góc ADB.

Bài 3: Cho tam giác ABC cân tại A có A = 100 độ. Qua B dựng tia Bx sao cho CBx = 30 độ. Tia phân giác của góc ACB cắt tia Bx tại D.

1. So sánh CD với CA
2. Tính số đo của góc BDA

Bài 4: Cho tam giác cân ABC (AB = AC) với BAC = 20 độ. Trên cạnh AC lấy điểm D sao cho CBD = 50 độ. Trên cạnh AB lấy điểm E sao cho BCE = 60 độ. Tính số đo góc CEB.

Bài 5: Cho tam giác ABC cân tại A có BAC = 80 độ. Gọi M là điểm nằm ngoài tam giác sao cho MBC = 10 độ, MCB = 30 độ. Tính số đo các góc AMB, AMC.

Bài viết trên đây vừa cung cấp cho các em thông tin hữu ích về cách tính số đo góc lớp 7, các dạng bài tập liên quan và cách giải. Chúc các em ôn tập hiệu quả và làm tốt bài thi sắp tới!