Tính chất giao hoán và kết hợp của phép nhân kèm bài tập

Tính chất giao hoán và kết hợp của phép nhân được hiểu là sẽ giúp ta tính toán nhanh hơn, vì có thể thay đổi thứ tự nhân các số mà không ảnh hưởng đến kết quả.

Trong toán học, phép nhân là một trong những phép tính quan trọng nhất. Nhưng bạn có biết rằng chúng cũng có một số đặc điểm mà chúng ta cần phải biết những tính chất để giải quyết các bài toán dễ dàng hơn .Tính chất của phép nhân cho biết phương pháp nhân một số không ảnh hưởng đến kết quả. Điều này rất hữu ích khi thực hiện các phép tính, chúng cho phép bạn sắp xếp các con số một cách tốt nhất có thể.

Mặt khác, tính chất của phép nhân cho phép chúng ta nhân các số theo bất kỳ cách nào chúng ta muốn trong khi kiểm tra kết quả cuối cùng. Trong bài viết này của thayphu chúng ta sẽ tìm hiểu sâu hơn về tính chất giao hoán và kết hợp của phép nhân và những điều xung quanh chúng.

Định nghĩa về tính chất giao hoán và kết hợp của phép nhân

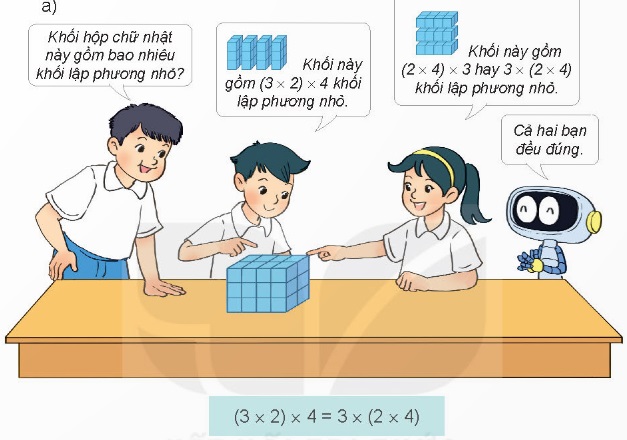
Định nghĩa về tính chất giao hoán và kết hợp của phép nhân

Những tính chất quan trọng của phép nhân được định nghĩa như sau

Tính chất giao hoán

Giải thích: Khi nhân hai số a và b, thứ tự của chúng không thay đổi kết quả. Thứ tự các số: a × b = b × a

Tính chất kết hợp

Giải thích: Khi nhân ba số a, b và c, thứ tự của phép nhân không quan trọng đối với kết quả.

Phương trình toán học: (a × b) × c = a × (b × c)

Ví dụ:

Tính chất giao hoán:

3 × 5 = 15

5 × 3 = 15

Kết quả giữ nguyên như nhau.

Tính chất kết hợp

(3 × 5) × 2 = 30

3 × (5 × 2) = 30

Kết quả giữ nguyên.

Ứng dụng của tính chất giao hoán và kết hợp trong thực tế

Tính chất giao hoán, kết hợp có nhiều ứng dụng hữu ích trong thực tế dưới đây chúng tôi đã tổng hợp những ứng dụng của chúng trong cuộc sống

Tính chất giao hoán

Tính nhanh: Khi tính toán, chúng ta có thể sắp xếp các số sao cho hợp lý nhất, rồi cộng lại với nhau và ra kết quả

Ví dụ: Khi tính 5 × 3 + 2 × 3, ta tính được các giá trị 5 × 3 = 15 và 2 × 3 = 6 rồi cộng chúng lại. Việc tính toán của phương pháp này nhanh hơn so với phép tính 2 × 3 + 5 × 3.

Đơn giản hóa biểu thức toán học: Chúng giúp chúng ta viết biểu thức toán học một cách đơn giản.

Ví dụ: b + a × c có thể viết lại thành a × (b + c).

Tính chất kết hợp

Hệ số nhân lớn: Hệ số nhân cho phép chúng ta chia phép nhân cho phép nhân, sau đó tạo từng số một và gộp chúng vào. Điều này rất hữu ích khi thực hiện các phép tính lớn.

Ví dụ: Muốn tính 5 × 7 × 3, ta có thể tính (5 × 7) × 3 hoặc 5 × (7 × 3), cả hai đều cho kết quả là 105.

Cải tiến tính toán: Tích hợp các tính năng giúp cải tiến thuật toán tính toán bằng cách đo các phép tính.

Chứng minh tính chất giao hoán và kết hợp của phép nhân

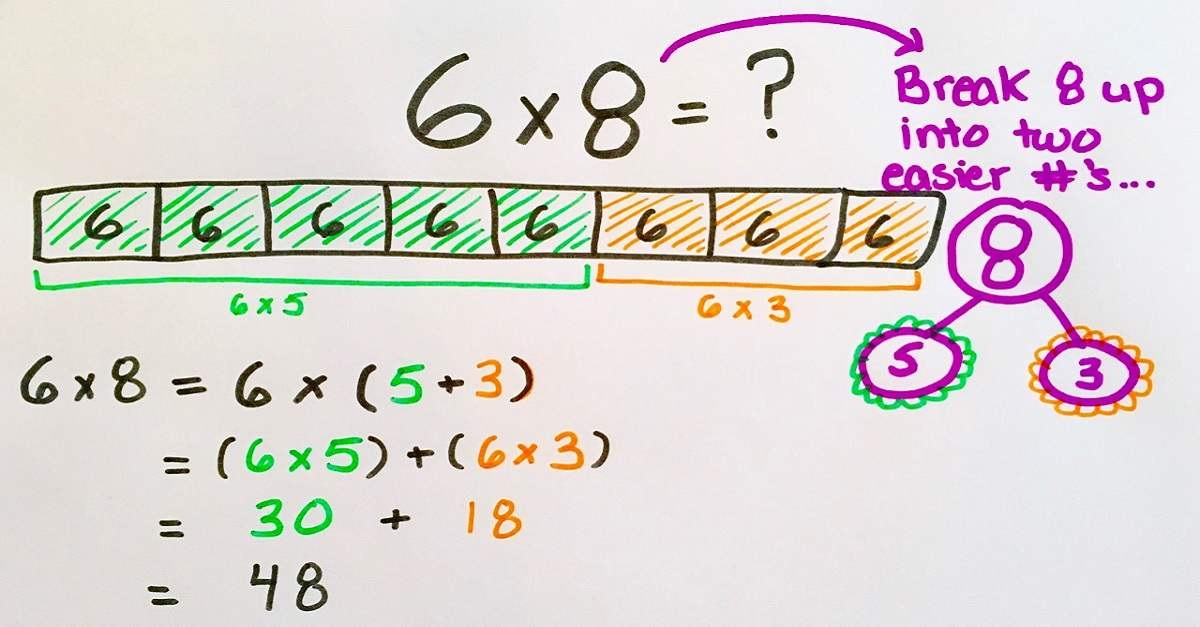
Chứng minh tính chất giao hoán và kết hợp của phép nhân

Dưới đây là những bước cụ thể giúp bạn dễ dàng chứng minh tính chất giao hoán, kết hợp

Chứng minh tính chất giao hoán

Chứng minh: a × b = b × a

Bước 1: Định nghĩa phép nhân

Theo định nghĩa, a × b = Σ (lần) b

Bước 2: Chứng minh

Giả sử a và b đều là số nguyên.

Theo định nghĩa phép nhân ta có:

a × b = Σ (lần) b

b × a = Σ (b lần) a

Bước 3: Sử dụng tính chất tăng

Vì Σ (lần) b = Σ (b) lần) a (vì phép cộng không phụ thuộc vào thứ tự) nên:

a × b = b × a

Bước 4: Kết quả

Như vậy ta đã chứng minh được tính chất giao hoán phép nhân.

Chứng minh tính chất kết hợp

Chứng minh: (a × b) × c = a × (b × c)

Bước 1: Định nghĩa phép nhân

Theo định nghĩa a × b = Σ (phép nhân) b

Bước 2: Chứng minh

Giả sử a, b và c là ba phần tử.

Theo định nghĩa phép nhân, ta có:

(a × b) × c = Σ ((a × b) lần) c

a × (b × c) = Σ (b × c)

Bước 3: Kết hợp và sử dụng các phần tử cộng chung

Vì Σ ((a × b) lần) c = Σ (lần) (b × c) (vì phép cộng không phụ thuộc vào thứ tự), nên

(a × b) × c = a × ( b × c) )

Bước 4: Kết quả

Như vậy, ta đã chứng minh được tính chất kết hợp của phép nhân.

Những dạng toán về tính chất giao hoán và kết hợp của phép nhân

Dưới đây là một số bài toán về tính chất giao hoán , kết hợp

Tính chất giao hoán

Tính chất giao hoán của phép nhân có nghĩa là a * b = b * a, với mọi a và b là các số thực.

Ví dụ:

1. Chứng minh rằng 3 * 5 = 5 * 3

Giải:

Trái: 3 * 5 = 15

Phải: 5 * 3 = 15

Vì 15 = 15, nên 3 * 5 = 5 * 3.

2. Chứng minh rằng a * b = b * a, với mọi a và b là các số thực.

Giải:

Giả sử a và b là hai số thực bất kỳ.

Theo định nghĩa của phép nhân, ta có: a * b = a × b.

Theo tính chất giao hoán của phép nhân, ta có: a × b = b × a.

Vậy a * b = b * a.

Tính chất kết hợp

Tính chất kết hợp của phép nhân có nghĩa là (a * b) * c = a * (b * c), với mọi a, b và c là các số thực.

Ví dụ:

1. Chứng minh rằng (2 * 3) * 4 = 2 * (3 * 4)

Giải:

Trái: (2 * 3) * 4 = 6 * 4 = 24

Phải: 2 * (3 * 4) = 2 * 12 = 24

Vì 24 = 24, nên (2 * 3) * 4 = 2 * (3 * 4).

2.Chứng minh rằng (a * b) * c = a * (b * c), với mọi a, b và c là các số thực.

Giải:

Giả sử a, b và c là ba số thực bất kỳ.

Theo định nghĩa của phép nhân, ta có: (a * b) * c = (a × b) × c.

Theo tính chất kết hợp của phép nhân, ta có: (a × b) × c = a × (b × c).

Vậy (a * b) * c = a * (b * c).

Bài tập áp dụng

Câu 1: Chọn câu đúng về tính chất giao hoán của phép nhân:

a) a * b = b * a, với mọi a và b là số thực

b) a * b ≠ b * a, với mọi a và b là số thực

c) a * b = a + b, với mọi a và b là số thực

Đáp án: a

Câu 2: Chọn câu sai về tính chất kết hợp của phép nhân:

a) (a * b) * c = a * (b * c), với mọi a, b và c là số thực

b) (a + b) + c = a + (b + c), với mọi a, b và c là số thực

c) (a * b) * c ≠ a * (b * c), với mọi a, b và c là số thực

Đáp án: c

Câu 3: Tính giá trị của biểu thức (2 * 3) * 5:

a) 10

b) 30

c) 50

Đáp án: a

Câu 4: Tính giá trị của biểu thức 2 * (3 * 5):

a) 10

b) 30

c) 50

Đáp án: b

Câu 5: Chọn câu đúng:

a) Tính chất giao hoán của phép nhân có nghĩa là a * b = a + b, với mọi a và b là số thực.

b) Tính chất kết hợp của phép nhân có nghĩa là (a * b) * c = a * (b + c), với mọi a, b và c là số thực.

c) Tính chất giao hoán và kết hợp của phép nhân đều đúng.

Đáp án: c

Câu 6: Chọn câu sai:

a) Tính chất giao hoán của phép nhân có nghĩa là a * b = b * a, với mọi a và b là số thực.

b) Tính chất kết hợp của phép nhân có nghĩa là (a * b) * c = a * (b * c), với mọi a, b và c là số thực.

c) Tính chất giao hoán và kết hợp của phép nhân không đúng với mọi a, b và c là số thực.

Đáp án: c

Câu 7: Tính giá trị của biểu thức (4 * 2) * 3:

a) 24

b) 36

c) 48

Đáp án: a

Câu 8: Tính giá trị của biểu thức 4 * (2 * 3):

a) 24

b) 36

c) 48

Đáp án: a

Câu 9: Chọn câu đúng:

a) Tính chất giao hoán của phép nhân có nghĩa là a * b = a + b, với mọi a và b là số thực.

b) Tính chất kết hợp của phép nhân có nghĩa là (a * b) * c = a * (b * c), với mọi a, b và c là số thực.

c) Tính chất giao hoán và kết hợp của phép nhân đều sai.

Đáp án: b

Câu 10: Chọn câu sai:

a) Tính chất giao hoán của phép nhân có nghĩa là a * b = b * a, với mọi a và b là số thực.

b) Tính chất kết hợp của phép nhân có nghĩa là (a * b) * c ≠ a * (b * c), với mọi a, b và c là số thực.

c) Tính chất giao hoán và kết hợp của phép nhân đều đúng.

Đáp án: b

Trong bài viết này, chúng ta đã học được hai tính chất quan trọng của phép nhân: tính chất giao hoán và tính chất kết hợp.

Các tính chất này đóng vai trò quan trọng trong việc tính toán và xử lý số. Chúng giúp chúng ta làm toán dễ dàng và hiệu quả. Biết những tính chất này có thể giúp bạn trở thành một nhà toán học giỏi hơn.

Thayphu.net hy vọng thông tin kèm với những ví dụ này sẽ giúp bạn hiểu rõ hơn về bản chất của sự tính chất giao hoán và kết hợp trong chương trình toán lớp 4. Nếu bạn có bất kỳ câu hỏi nào khác xin vui lòng liên hệ với chúng tôi nhé.