Tính chất phân số, ứng dụng và cách giải các bài tập dễ hiểu

Nắm vững tính chất phân số sẽ giúp các em dễ dàng vận dụng làm tốt các bài tập. Tham khảo các nội dung hữu ích để hoàn thành nội dung Toán lớp 4.

Các kiến thức cơ bản về tính chất phân số là nội dung quan trọng trong chương trình Toán lớp 4. Hãy cùng thayphu ôn tập lại ngay qua bài viết này và thực hành giải bài tập một cách nhanh chóng, dễ hiểu nhất nhé!

Tính chất phân số Toán lớp 4

Lý thuyết về các tính chất cơ bản của phân số

Tính chất 1: Nếu ta nhân cả tử số và mẫu số của 1 phân số với cùng 1 số tự nhiên khác 0 thì ta sẽ được 1 phân số mới bằng phân số đã cho.

Ví dụ minh họa: ⅓ = (1 x 2) / (3 x 2) = 2/6

Tính chất 2: Nếu chia cả tử số và mẫu số của 1 phân số cho cùng 1 số tự nhiên khác 0 thì ta được 1 phân số mới bằng với phân số đã cho.

Ví dụ minh họa: 5/10 = 5:5 / 10:5 = ½

Ứng dụng tính chất phân số như thế nào?

Các tính chất cơ bản của phân số được ứng dụng trong các trường hợp:

Rút gọn phân số

Khi tiến hành rút gọn phân số ta sẽ được 1 phân số có tử số và mẫu số bé đi mà phân số mới vẫn bằng với phân số đã cho ban đầu.

Cụ thể các bước rút gọn phân số như sau:

• Đầu tiên ta xét xem cả tử số và mẫu số của phân số đó có cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Tiếp theo là chia cả tử số và mẫu số của phân số đó cho số tự nhiên vừa tìm được.
• Cuối cùng ta cứ thực hiện cho đến khi tìm được phân số tối giản nhất.

Chú ý: Chúng ta phải rút gọn phân số cho đến khi không thể rút gọn được nữa. Tức là khi đã nhận được phân số tối giản. Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho bất kỳ số tự nhiên nào khác 1.

Ví dụ minh họa:

Rút gọn phân số 18/27

Ta xét 18 và 27 đều chia hết cho 3, nên:

18/27 = (18 : 3) / (27 : 3) = 6/9

Tuy nhiên cả 6 và 9 đều vẫn có thể chia hết cho 3 nên phải rút gọn tiếp:

6/9 = (6 : 3) / (9 : 3) = ⅔ (⅔ là phân số tối giản)

Chú ý: Có nhiều cách rút gọn phân số nhưng cách nhanh nhất là ta chọn đúng số lớn nhất mà tử số và mẫu số của phân số đã chia đều hết cho số đó.

Chẳng hạn như với phân số 18/27, ngoài 3 ra thì cả tử số và mẫu số đều chia hết cho 9.

18/27 = (18 : 9) / (27 : 9) = ⅔

Quy đồng mẫu số các phân số

Quy đồng mẫu số nghĩa là biến các phân số có mẫu số khác nhau về dưới dạng phân số có cùng mẫu số. Với các mẫu số khác nhau, ta thường quy đồng mẫu số theo 2 bước:

• Bước 1: Đầu tiên lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ 2
• Bước 2: Tiếp theo lấy tử số và mẫu số của phân số thứ 2 nhân với mẫu số của phân số thứ nhất.

Ví dụ minh họa: Quy đồng mẫu số của 2 phân số ⅖ và 4/7

Ta được kết quả: ⅖ = (2 x 7) / (5 x 7) = 14/35

4/7 = (4 x 5) / (7 x 5) = 20 / 35

=> Như vậy 2 phân số mới đó là 14/35 và 20/35.

Trường hợp đặc biệt 1:

• Nếu như các mẫu số đã cho có 1 mẫu số nào chia hết cho tất cả các mẫu số còn lại thì đó là mẫu số chung.
• Ta dùng mẫu số chung chia cho các mẫu số còn lại để tìm thừa số phụ.
• Rồi nhân cả tử số và mẫu số của các phân số còn lại với thừa số phụ tương ứng.
• Cuối cùng giữ nguyên phân số có mẫu số chia hết cho các mẫu số kia.

Ví dụ minh họa: Quy đồng mẫu số của ⅖ và 3/10

Ta có 10 chia hết cho 5 nên mẫu số chung của 2 phân số này là 10

Vì 10 : 5 = 2 nên ta dùng cả tử và mẫu số của ⅖ nhân với thừa số phụ là 2

⅖ = (2 x 2) / (5 x 2) = 4/10

Giữ nguyên phân số 3/10

=> Vậy kết quả quy đồng mẫu số ta được 4/10 và 3/10.

Trường hợp đặc biệt 2:

• Nếu các mẫu số đã cho không có mẫu số nào chia hết cho các mẫu số còn lại thì mẫu số chung là số tự nhiên nhỏ nhất khác 0 và cùng chia hết cho các mẫu số còn lại.
• Ta lấy mẫu số chung chia cho các mẫu số còn lại để tìm thừa số phụ.
• Rồi nhân cả tử và mẫu số của các phân số còn lại với thừa số phụ tương ứng.

Ví dụ minh họa: Quy đồng ½, ⅔ và ¾

Tích của 3 mẫu số trên là 2 x 3 x 4 = 24 nhưng ta không lấy 24

Mà có 12 chia hết cho cả 2, 3, 4 nên mẫu số chung của 3 phân số đó là 12.

Vì 12 : 2 = 6 ta lấy ⅓ nhân với thừa số phụ là 6 sẽ được: ½ = (1x6) / (2x6) = 6/12

Vì 12 : 3 = 4 ta lấy ⅔ nhân với thừa số phụ là 4 sẽ được: ⅔ = (2x4) / (3x4) = 8/12

Vì 12 : 4 = 3 ta lấy ¾ nhân với thừa số phụ là 3 sẽ được: ¾ = (3x3) / (4x3) = 9/12

Giải bài tập SGK về tính chất phân số lớp 4

Sau khi tìm hiểu các tính chất phân số hãy cùng thực hành giải các bài tập cơ bản sau đây:

Giải các bài tập về tính chất của phân số lớp 4

Bài tập 1

Điền số thích hợp vào chỗ chấm:

1. 3/7 = (3x4) / (7x4) = … / …

2/9 = (2x3) / (9x3) = … / …

15/46 = (15x7) / (46x7) = … / …

2. 28/60 = (28:4) / (60:4) = … / …

48/56 = (48:8) / (56:8) = …/…

125/75 = (125:25) / (75:25) = …/…

Lời giải:

1. 3/7 = (3x4) / (7x4) = 12/28

2/9 = (2x3) / (9x3) = 6/27

15/46 = (15x7) / (46x7) = 105/322

2. 28/60 = (28:4) / (60:4) = 7/15

48/56 = (48:8) / (56:8) = 6/7

125/75 = (125:25) / (75:25) = 5/3

Bài tập 2

Cho phân số 60/95, cùng giảm 5 lần tử số và mẫu số ta sẽ được phân số nào? Hãy chọn đáp án đúng trong kết quả sau:

1. 12/95

2. 60/19

3. 12/19

4. 19/12

Lời giải:

Ta có 60/95 = (60:50) / (95:5) = 12/19

Như vậy phân số 60/95 sau khi giảm đi 5 lần cả tử số và mẫu số thì ta được phân số mới là 12/19.

Kết luận đáp án đúng là C.

Bài tập 3

Điền số thích hợp vào chỗ chấm:

1. ⅝ = …/16

2. 24/30 = …/5

3. …/18 = ⅚

4. 7/12 = …/48

Lời giải:

1. ⅝ = 10/16

2. 24/30 = ⅘

3. 15/18 = ⅚

4. 7/12 = 28/48

Bài tập 4

Mỗi hình vuông, hình tam giác, hình tròn che khuất 1 số trong các phân số như hình:

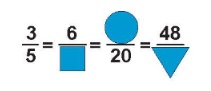
Cộng các số bị che lấp bởi 3 hình ta sẽ được kết quả là…

Lời giải:

Ta có ⅗ = 6/10 = 12/20 = 48/80

Như vậy hình vuông là số 10, hình tròn là 12, hình tam giác là 80.

Cộng tất cả các số bị che lấp bởi 3 hình đó là: 10 + 12 + 80 = 102.

Bài tập 5

Cho các phân số 4/6, 3/2, 8/12, ⅔

Hãy tìm các phân số bằng nhau?

Lời giải:

Ta có: 4/6 = (4x2) / (6x2) = ⅔

8/12 = (8:4) / (12:4) = ⅔

Như vậy các phân số bằng nhau là 4/6; 8/12; ⅔.

Trên đây là bài viết của thayphu.net tổng hợp các tính chất phân số, ví dụ minh họa cùng lời giải các bài tập chi tiết nhất. Các em hãy cùng ôn tập và thực hành để nắm vững nội dung này. Đừng quên truy cập vào chuyên mục Toán 4 để theo dõi các bài học mới nhất nhé!