Tính chất 2 tiếp tuyến cắt nhau, tổng hợp kiến thức và bài tập

Tổng hợp lý thuyết căn bản về tính chất 2 tiếp tuyến cắt nhau. Các dạng bài tập thường gặp kèm lời giải chi tiết, dễ hiểu nhất.

Tính chất 2 tiếp tuyến cắt nhau là một trong những nội dung đáng chú ý của chương trình Toán lớp 9. Để làm tốt các dạng bài tập hình học các em phải nắm vững phần kiến thức cơ bản. Hãy cùng thay phu ôn lại lý thuyết và tham khảo những dạng bài tập thường gặp sau đây nhé!

Lý thuyết về tính chất 2 tiếp tuyến cắt nhau

Định lý 2 tiếp tuyến cắt nhau

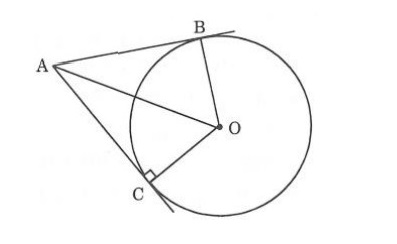
Nếu như 2 tiếp tuyến của một đường tròn cắt nhau tại một điểm thì ta có:

• Điểm đó sẽ cách đều 2 tiếp điểm
• Tia kẻ từ điểm đó đi qua tâm đường tròn là tia phân giác của góc tạo bởi 2 tiếp tuyến.
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi 2 bán kính qua các tiếp điểm.

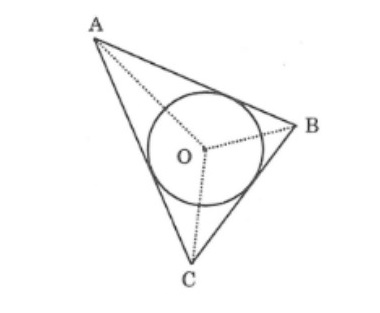
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả 3 cạnh của 1 tam giác. Còn tam giác được gọi là ngoại tiếp đường tròn. Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác góc trong tam giác.

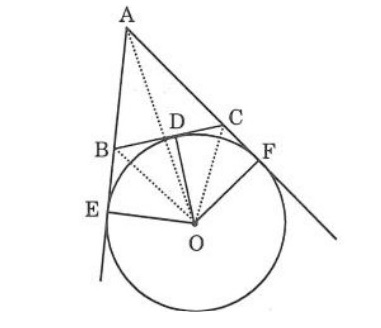
Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với 1 cạnh của tam giác và tiếp xúc với 2 phần kéo dài của 2 cạnh kia. Tâm đường tròn bàng tiếp tam giác trong góc A là giao điểm của 2 đường phân giác của các góc ngoài tại điểm B và C. Hoặc là giao điểm của đường phân giác của góc trong A và đường phân giác góc ngoài tại B (hoặc C). Có 3 đường tròn bàng tiếp trong 1 tam giác.

Các dạng bài tập về tính chất 2 tiếp tuyến cắt nhau

Sau khi ôn lại một số lý thuyết, hãy cùng thực hành với các dạng bài tập thường gặp dưới đây. Đi kèm với đó là cách giải chi tiết cho các em cùng tham khảo nhé!

Dạng 1 - Chứng minh các đường thẳng song song, vuông góc với nhau

Phương pháp giải: Chúng ta sẽ áp dụng định lý tính chất của 2 tiếp tuyến cắt nhau ở phần trên.

Bài 1

Cho đường tròn tâm O với A là điểm nằm ngoài đường tròn. Tiếp tục kẻ các tiếp tuyến AB và AC với đường tròn (trong đó B, C là các tiếp điểm). Hãy chứng minh rằng:

1. Đoạn thẳng OA vuông góc với đoạn thẳng BC
2. Vẽ đường kính CD. Chứng minh BD // AO
3. Tìm độ dài các cạnh của ΔABC biết OB = 2cm; OA = 4cm.

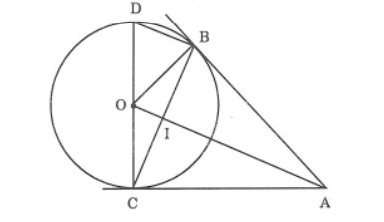
Cách giải:

1. Muốn chứng minh đoạn OA vuông góc với BC ta phải chứng minh được ΔABC cân tại A.

Xét ΔABC ta có:

AB = AC vì AB và AC là 2 tiếp tuyến của đường tròn (O) cắt nhau tại A

Theo định lý, nếu 2 tiếp tuyến của đường tròn cắt nhau tại 1 điểm thì nó cách đều 2 tiếp điểm

=> ΔABC cân tại A (Tam giác có 2 cạnh bằng nhau là tam giác cân)

Suy ra đường phân giác AO của góc BAC lại là đường cao ứng với đáy BC.

Vì vậy AO vuông góc với BC (1)

2. Trong ΔBCD có OB = OD = OC = CD/2 (đều là bán kính đường tròn tâm O)

Áp dụng định lý ta có ΔBCD vuông tại B.

=> BD vuông góc với BC (2)

Từ (1) và (2) ta kết luận BD // AO.

3. Áp dụng định lý Py-ta-go ta có:

ΔBOA vuông tại B nên OA^2 = OB^2 + AB^2

⇔ AB^2 = OA^2 - OB^2 => AB^2 = 4^2 - 2^2 = 16 - 4 = 12

=> AB = 12 = 4.3 = 23 cm

ΔOBA vuông tại B có OB = OD = OC = OA/2 = ½.4 = 2cm

Như vậy OBA là nửa tam giác đều.

=> OAB = 30 độ => BAC = 2OAB = 2.30 độ = 60 độ

=> ΔABC là tam giác đều nên AB = BC = CA = 23 cm.

Bài 2

Từ một điểm A nằm ngoài đường tròn tâm O ta kẻ các tiếp tuyến AB và AC với đường tròn (với B,C là tiếp điểm). Qua điểm M thuộc cung nhỏ BC kẻ tiếp tuyến với đường tròn tâm O. Nó cắt tiếp tuyến AC, AC lần lượt ở điểm D và E. Chứng minh chu vi ΔADE = 2AB.

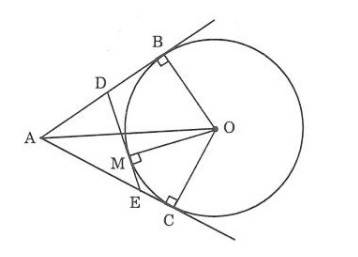
Cách giải:

Sử dụng định lý tính chất 2 tiếp tuyến cắt nhau ta có:

DM = DB, EM = EC và AB = AC

=> chu vi ΔADE = AD + DE + EA = AD + DM + EM + AE

= AB + BD + EC + AE = 2AB (vì AB = AC).

Dạng 2 - Chứng minh đường thẳng là tiếp tuyến, tính độ dài, số đo góc

Phương pháp giải: Đối với dạng bài này ta áp dụng 1 trong các lý thuyết sau:

• Định nghĩa tiếp tuyến, tính chất của 2 tiếp tuyến cắt nhau
• Khái niệm đường tròn nội tiếp, bàng tiếp tam giác
• Hệ thức lượng về cạnh và góc trong 1 tam giác vuông.

Bài 1

Cho góc xAy không phải là góc bẹt và điểm B thuộc tia Ax. Yêu cầu dựng đường tròn tâm O tiếp xúc với đường thẳng Ax tại B và tiếp xúc với đường thẳng Ay.

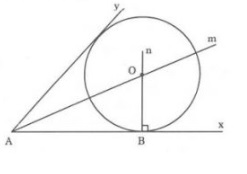
Cách giải:

Theo tính chất đường phân giác của một góc ta sẽ có cách dựng như sau:

• Vẽ tia phân giác Am của xAy
• Vẽ Bn vuông góc Ax tại B
• Bn cắt Am tại O
• Vẽ đường tròn tâm O, bán kính OB là đường tròn phải dựng. Đường tròn này tiếp xúc với Ay vì O cách đều Ax và Ay.

Bài 2

Cho nửa đường tròn tâm O với đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ là AB). Từ M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn và cắt Ax, By lần lượt tại C và D.

1. Chứng minh góc COD là góc vuông
2. Chứng minh CD = AC + BD

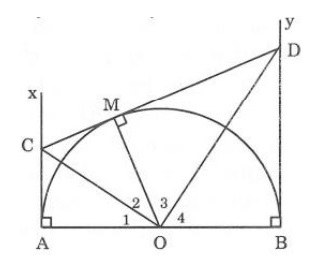
Cách giải:

1. Áp dụng định lý về tính chất 2 tiếp tuyến cắt nhau ta có:

O1 = O2 và O3 = O4 mà O1 + O2 + O3 + O4 = 180 độ

nên O1 + O2 + O3 + O4 = 180 độ / 2 = 90 độ.

Vậy góc COD = 90 độ và là góc vuông.

2. Biết CD = CM + MD

Ta thấy muốn có CD = AC + BD phải xuất hiện 2 đẳng thức. Từ 2 đẳng thức vừa có ta cộng vế với vế thì được điều phải chứng minh.

Theo định lý về 2 tiếp tuyến của 1 đường tròn cắt nhau tại 1 điểm ta có:

CM + DM = CA + BD

CM + MD = AC + BD => CD = AC + BD.

Bài viết vừa cung cấp các thông tin về lý thuyết cũng như các dạng bài tập thường gặp về tính chất 2 tiếp tuyến cắt nhau. Hy vọng các em có những phút giây học tập hiệu quả và đạt nhiều điểm tốt!