Rút gọn biểu thức chứa căn, phương pháp và dạng toán cơ bản

Biểu thức chứa căn là gì? Các quy tắc cơ bản, phương pháp và bài tập ôn luyện về dạng toán rút gọn biểu thức chứa căn trong chương trình toán lớp 9.

Trong toán học, đặc biệt là chương trình toán lớp 9, khi làm việc với biểu thức chứa căn, việc rút gọn biểu thức có thể giúp chúng ta đơn giản hóa và tối ưu hóa phép tính. Rút gọn biểu thức chứa căn đòi hỏi chúng ta áp dụng các quy tắc và công thức đúng để giải các bài toán liên quan đến căn.

Vì vậy, trong bài viết này, thayphu sẽ cùng các bạn học sinh tìm hiểu về cách rút gọn một biểu thức chứa căn một cách hiệu quả.

Biểu thức chứa căn là gì?

Biểu thức chứa căn là một biểu thức trong toán học mà trong đó chứa ít nhất một biểu thức căn bậc hai (√), căn bậc ba (∛), hoặc căn bậc n (∛n) với n là một số nguyên dương. Các biểu thức này có thể chứa các phép tính toán học khác như cộng, trừ, nhân, chia, lũy thừa, và các biến số.

Ví dụ về các biểu thức chứa căn:

√(x + 4)

2√(3x - 7)

∛(8y^2 + 2y - 1)

√(a^2 + b^2) + √(a^2 - b^2)

Các quy tắc cơ bản về biểu thức chứa căn

• Quy tắc nhân căn: √(a * b) = √a * √b.
• Quy tắc chia căn: √(a / b) = √a / √b.
• Quy tắc lũy thừa căn: (√a)^n = √(a^n).
• Quy tắc căn bậc hai của tổ hợp và chữ số mũ.
  • √(a + b) không thể biến đổi thành √a + √b
  • √(a - b) không thể biến đổi thành √a - √b
  • √(a^2 + b^2) không thể biến đổi thành √a^2 + √b^2

Phương pháp để rút gọn một biểu thức chứa căn

Phương pháp 1: Tách căn thành các thành phần nhỏ hơn

Trong một biểu thức chứa căn, chúng ta có thể tách căn thành các thành phần nhỏ hơn để dễ dàng rút gọn. Sử dụng quy tắc nhân căn và chia căn, từ đó có thể phân tích các căn thành các căn nhỏ hơn.

Ví dụ: Rút gọn biểu thức √(12)

Phân tích 12 thành 4 và 3: √(12) = √(4 * 3)

Sử dụng quy tắc nhân căn, chúng ta có: √(4 * 3) = √4 * √3 = 2√3

Vậy biểu thức √(12) đã được rút gọn thành 2√3.

Phương pháp 2: Sử dụng quy tắc lũy thừa căn

Nếu trong biểu thức chứa căn có lũy thừa căn, chúng ta có thể áp dụng quy tắc lũy thừa căn để rút gọn biểu thức. Điều này giúp chúng ta đơn giản hóa biểu thức và thực hiện các phép tính một cách hiệu quả.

Ví dụ: Rút gọn biểu thức (√2)^3

Sử dụng quy tắc lũy thừa căn, chúng ta có: (√2)^3 = √(2^3) = √8

Tiếp theo, chúng ta có thể tách căn 8 thành căn 4 và căn 2: √8 = √(4 * 2) = √4 * √2 = 2√2

Vậy, biểu thức (√2)^3 đã được rút gọn thành 2√2.

Các dạng toán cơ bản về rút gọn biểu thức

Dạng 1: Rút gọn căn bậc hai, căn bậc ba

Sử dụng quy tắc nhân căn: Nếu trong biểu thức có tích của các căn bậc hai hoặc căn bậc ba, chúng ta có thể sử dụng quy tắc nhân căn để rút gọn biểu thức.

Ví dụ:

√(ab) = √a * √b

∛(abc) = ∛a * ∛b * ∛c

Sử dụng quy tắc chia căn: Nếu trong biểu thức có phép chia của các căn bậc hai hoặc căn bậc ba, chúng ta có thể sử dụng quy tắc chia căn để rút gọn biểu thức.

Ví dụ:

√(a/b) = √a / √b

∛(a/b) = ∛a / ∛b

Dạng 2: Rút gọn biểu thức kết hợp căn

Sử dụng quy tắc phân phối căn: Nếu trong biểu thức có sự phân phối của căn, chúng ta có thể sử dụng quy tắc phân phối căn để rút gọn biểu thức.

Ví dụ: √(a + b) * √(a - b) = √((a + b) * (a - b))

Sử dụng quy tắc chuyển đổi căn: Nếu trong biểu thức có căn bậc hai và căn bậc ba, chúng ta có thể sử dụng quy tắc chuyển đổi căn để rút gọn biểu thức.

Ví dụ: √(∛a^2) = a^(2/3)

Trên đây chỉ là một số dạng và ví dụ cơ bản về việc rút gọn biểu thức chứa căn. Trong thực tế, có nhiều quy tắc và phương pháp khác nhau tùy thuộc vào cấu trúc và yêu cầu của biểu thức.

Bài tập vận dụng và ôn luyện

Bài tập 1: Hai biểu thức chứa căn với x ≥ 0; x ≠ 1.

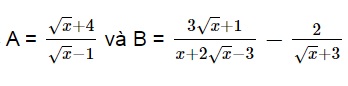
1. Tính giá trị của biểu thức A khi cho x = 9.

2. Hãy chứng minh

​

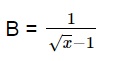
Gợi ý lời giải:

Bài tập 2: Rút gọn biểu thức sau với x ≥ 0; x ≠ 1.

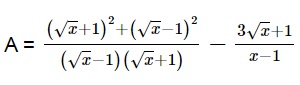
Gợi ý lời giải:

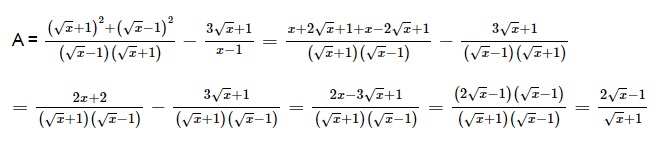
Rút gọn biểu thức chứa căn là một kiến thức tuy cơ bản nhưng rất quan trọng trong toán lớp 9. Áp dụng quy tắc nhân căn, chia căn, và quy tắc lũy thừa căn, chúng ta có thể đơn giản hóa và tối ưu hóa biểu thức chứa căn. Việc rút gọn biểu thức giúp chúng ta hiểu rõ hơn về cấu trúc của biểu thức và thực hiện các phép tính một cách hiệu quả. Vì vậy, hãy áp dụng các quy tắc và phương pháp được đề cập trong bài viết này để rút gọn biểu thức chứa căn một cách chính xác và tỉ mỉ. Và hãy ôn tập thật chăm chỉ để có một nền tảng thật tốt, bởi lẽ lớp 9 là 1 trong những cột mốc quan trọng của học sinh chuẩn bị bước vào kỳ thi tuyển sinh 10.