Lý thuyết và dạng bài tập tỉ số lượng giác trong tam giác vuông

Kiến thức cơ bản về tỉ số lượng giác trong tam giác vuông. Cách tính cạnh, tính góc, tính tỉ số lượng giác dựa vào dữ kiện đề bài.

Trong chương trình Toán hình lớp 9, tỉ số lượng giác trong tam giác vuông là một kiến thức đặc biệt cần nắm chắc. Bài viết sau đây sẽ cung cấp cho các em đầy đủ từ phần lý thuyết, tính chất, cách tính tỉ số lượng giác và các bài tập áp dụng. Hãy cùng thayphu theo dõi ngay bài viết nhé!

Lý thuyết về tỉ số lượng giác trong tam giác vuông

Tỉ số lượng giác của góc nhọn trong tam giác vuông là các tỉ số về các cạnh của góc nhọn xuất hiện trong tam giác vuông. Theo đó, tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc α, kí hiệu là sin α. Tỉ số của cạnh kề và cạnh huyền sẽ là cô-sin của góc α, kí hiệu là cos α. Tỉ số giữa cạnh đối và cạnh kề ta gọi là tang của góc α, kí hiệu là tan α. Tỉ số giữa cạnh kề và cạnh đối gọi là cô-tang của góc α, kí hiệu là cot α.

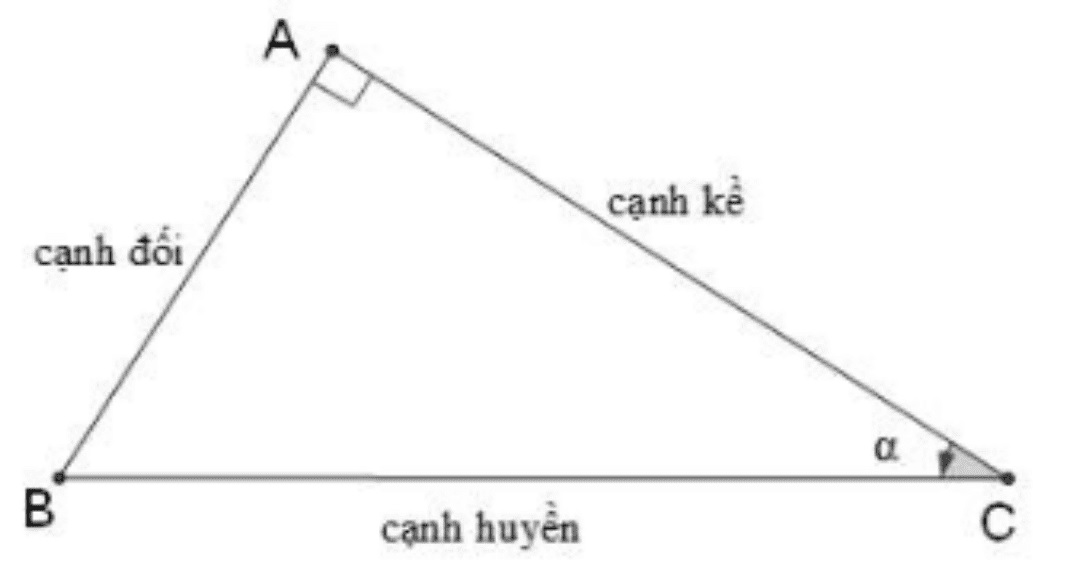
Tam giác ABC vuông tại A

Công thức tỉ số lượng giác

Cho tam giác vuông ABC (như hình) và góc ACB = α, ta có:

• sin α = cạnh đối / cạnh huyền = AB/BC
• cos α = cạnh kề / cạnh huyền = AC/BC
• tan α = cạnh đối / cạnh kề = AB/AC
• cot α = cạnh kề / cạnh đối = AC /AB

Tính chất của tỉ số lượng giác trong tam giác vuông

• Tỉ số lượng giác của một góc nhọn luôn dương. Đặc biệt 0 < sin α và cos α < 1.
• Tỉ số lượng giác của 2 góc phụ nhau

Nếu 2 góc nhọn phụ nhau thì sin của góc này sẽ bằng cosin của góc kia và tan góc này sẽ bằng cotang của góc kia. Cụ thể là khi cho góc nhọn α ta sẽ có:

sin α = cos (90 độ -α) tan α = cot (90 độ -α)

cos α = sin (90 độ -α) cot α = tan (90 độ -α)

• sin α = sinβ góc α = góc β
• Trường hợp khi góc α tăng từ 0 độ đến 90 độ thì sin α, tan α tăng còn cos α, cot α giảm.

Cụ thể: Khi cho 2 góc nhọn α và β thì ta được:

sin α > sin β góc α > góc β

tan α > tan β góc α > góc β

cos α < cosβ góc α > góc β

cot α < cotβ góc α > góc β

Lý thuyết về tỉ số lượng giác trong tam giác vuông

Hệ thức

Thứ nhất: Hệ thức giữa cạnh và góc trong tam giác vuông

Cạnh góc vuông sẽ bằng cạnh huyền nhân sin góc đối hoặc cạnh huyền nhân cos góc kề.

Cạnh góc vuông sẽ bằng cạnh góc vuông còn lại nhân tan góc đối hoặc cạnh góc vuông còn lại nhân cotan góc kề.

Thứ 2: Hệ thức giữa các tỉ số lượng giác của góc nhọn

• sin^2 α + cos^2 α = 1
• tan α = sin α / cos α
• cot α = cos α / sin α
• tan α. cot α = 1
• 1/sin^2 α = 1 + cot^2 α
• 1/cos^2 α = 1 + tan^2 α

Các dạng bài tập về tỉ số lượng giác trong tam giác vuông

Sau khi tìm hiểu về lý thuyết căn bản, chúng ta cùng bắt ngay vào thực hành với các dạng bài tập để hiểu rõ và ghi nhớ tốt hơn nhé!

Các dạng bài tập thường gặp và cách giải chi tiết

Dạng 1 - Tính các tỉ số lượng giác, các góc và cạnh trong tam giác

Ví dụ: Cho tam giác ADM vuông tại điểm D, yêu cầu tìm các tỉ số lượng giác của góc A khi:

1. AM = 5cm, AD = 4cm
2. AM = 13cm, DM = 12cm

Hướng dẫn giải:

1. Xét tam giác ADM vuông tại D, theo định lý Pytago ta có:

AD^2 + DM^2 = AM^2 ⇔ 4^2 + DM^2 = 5^2

⇔ DM^2 = 5^2 - 4^2

⇔ DM^2 = 9

⇔ DM = 3

Như vậy ta sẽ được: sin A = DM/AM = ⅗

cos A = AD/AM = ⅘

tan A = DM/AD = ¾

cot A = AD/DM = 4/3.

2. Xét tam giác vuông ADM, theo định lý Pytago ta có:

AD^2 + DM^2 = AM^2 ⇔ AD^2 + 12^2 = 13^2

⇔AD^2 = 25 ⇔ AD = 5.

Như vậy là:

sin A = DM/AM = 12/13

cos A = AD/AM = 5/13

tan A = DM/AD = 12/5

cot A = AD/DM = 5/12

Dạng 2 - Chứng minh đẳng thức lượng giác

Ví dụ 1: Cho tam giác ADM vuông tại điểm D, yêu cầu chứng minh AD/DM = sin M/sin A.

Hướng dẫn giải:

Xét tam giác vuông ADM, ta có:

sin A = DM/AM; sin M = AD/AM

=> sin M/ sin A = AD/AM : DM/AM = AD/DM

Như vậy kết luận AD/DM = sin M = sin A.

Ví dụ 2: Cho tam giác AMN có góc A = 60 độ, hãy chứng minh rằng MN^2 = AM^2 + AN^2 -AM. AN

Hướng dẫn giải:

Ta kẻ MH vuông góc với cạnh AN.

Xét tam giác vuông MHN vuông tại điểm H, ta được:

MN^2 = MH^2 + HN^2

MN^2 = MH^2 + (AN - AH)^2

MN^2 = MH^2 + AH^2 + AN^2 -2.AN.AH

MN^2 = MA^2 + AN^2 - 2AN.AH (1)

Tiếp tục xét tam giác vuông AMH vuoog tại H ta có:

cos góc MAH = AH/AM

AH= AM. cos60 = AM/2

Thay vào (1) ta sẽ được: MN^2 = AM^2 + AN^2 - AM. AN

Kết luận MN^2 = AM^2 + AN^2 - AM. AN

Dạng 3 - Rút gọn biểu thức

Ví dụ: Yêu cầu rút gọn các biểu thức sau:

1. A = sin^4 a + cos^4 a + 2sin^2 a. cos^2 a

= (sin^2 a + cos^2 a)^2

= 1

2. B = tan^2 a - sin^2 a. tan^2 a

= tan^2 a. (1 - sin^2 a)

= tan^2 a. cos^2 a

= sin^2 α / cos^2 α . cos^2 a

= sin^2 a

3. C = cos^2 a. cos^2 b + cos^2 a. sin^2 b + sin^2 a

= cos^2 a. (cos^2 b + sin^2 b) + sin^2 a

= cos^2 a + sin^2 a

= 1

4. D = 2(sin a - cos a)^2 - (sin a + cos a)^2 + 6 sin a. cos a

= 2. (sin^2 a - 2sin a. cos a + cos^2 a) - (sin^2 a + 2sin a.cos a + cos^2 a) + 6sin a. cos a

= 2sin^2 a - 4sin a. cos a + 2cos^2 a - sin^2 a - 2sin a. cos a - cos^2 a + 6sin a. cos a

= sin^2 a + cos^2 a = 1

Trên đây là tổng hợp các kiến thức và các dạng bài tập về tỉ số lượng giác trong tam giác vuông. Hy vọng các em có thể ghi nhớ và vận dụng giải thành thạo các bài toán. Chúc các em học tốt và đừng quên theo dõi kênh để cập nhật thêm nhiều bài học hay nhé!