Phương pháp giải phương trình trùng phương và bài tập áp dụng

Các em cùng bỏ túi ngay các phương pháp giải phương trình trùng phương hiệu quả này để dễ dàng hoàn thành tốt bài tập và đề thi.

Phương trình trùng phương là dạng phương trình thường gặp trong nội dung chương trình toán lớp 9. Để giúp các em nhanh chóng hiểu rõ về lý thuyết cũng như biết cách giải loại phương trình này, bài viết sau đây của thayphu sẽ tổng hợp đầy đủ kiến thức nhất về chủ đề trên. Hãy cùng tìm hiểu ngay nhé!

Lý thuyết về phương trình trùng phương

Tìm hiểu về phương trình trùng phương

Phương trình trùng phương là phương trình bậc 4 có dạng ax^4 + b^2 + c = 0 với a khác 0. Đây thực chất là phương trình bậc 2 có ẩn là x^2.

Với Δ = b^2 - 4ac khi đó:

• Phương trình ax^4 + b^2 + c = 0 có duy nhất 1 nghiệm ⇔ c = 0 và b/a <= 0, nghiệm = 0
• Phương trình ax^4 + b^2 + c = 0 có 2 nghiệm phân biệt ⇔ Δ = 0 và b/a < 0 hoặc Δ>0 hoặc c/a < 0
• Phương trình ax^4 + b^2 + c = 0 có 3 nghiệm phân biệt ⇔ c = 0 và b/a < 0, trong đó có 1 nghiệm = 0
• Phương trình ax^4 + b^2 + c = 0 có 4 nghiệm phân biệt ⇔ Δ > 0, b/a < 0 và c/a > 0. Như vậy tổng 4 nghiệm = 0 và tích 4 nghiệm = c/a
• Phương trình ax^4 + b^2 + c = 0 vô nghiệm ⇔ Δ < 0 hoặc Δ >= 0, b/a > 0, c/a < 0.

Phương pháp giải phương trình trùng phương bằng cách đặt ẩn phụ

Sau khi tìm hiểu cơ bản về lý thuyết, các em sẽ cùng xem các phương pháp giải để vận dụng khi làm bài tập.

Các phương pháp giải phương trình bậc 4 chi tiết

Cách thực hiện

Cho phương trình ax^4 + bx^2 + c = 0 với a khác 0 (1)

Đặt t = x^2 (với t>=0) khi đó phương trình có dạng at^2 + bt + c = 0 (2)

• Trường hợp phương trình (2) có 2 nghiệm dương thì phương trình (1) có 4 nghiệm.
• Trường hợp phương trình (2) có 1 nghiệm dương, 1 nghiệm âm hoặc có nghiệm kép dương thì phương trình (1) có 2 nghiệm.
• Trường hợp phương trình (2) có 2 nghiệm âm hoặc vô nghiệm thì phương trình (1) vô nghiệm.

Cụ thể:

• Phương trình (1) có 4 nghiệm phân biệt ⇔ Phương trình (2) sẽ có 2 nghiệm phân biệt đều dương ⇔ Δ > 0, P > 0, S > 0.
• Phương trình (1) có 3 nghiệm phân biệt ⇔ Phương trình (2) có 1 nghiệm dương và 1 nghiệm bằng 0 ⇔ Δ > 0, P = 0, S > 0.
• Phương trình (1) có 2 nghiệm phân biệt ⇔ Phương trình (2) có 1 nghiệm kép dương hoặc 2 nghiệm trái dấu. Tương đương Δ = 0, S > 0 hoặc Δ > 0, P < 0 ⇔ Δ = 0 và S > 0 hoặc a.c < 0.
• Phương trình (1) có 1 nghiệm ⇔ Phương trình (2) có 1 nghiệm kép = 0 hoặc 1 nghiệm = 0 và nghiệm còn lại âm. Tương đương Δ = 0, S = 0, P = 0 hoặc Δ > 0, S < 0, P= 0.
• Phương trình (1) vô nghiệm ⇔ Phương trình (2) vô nghiệm hoặc có 2 nghiệm âm ⇔ Δ < 0 hoặc Δ > 0, P > 0, S < 0.
• Trường hợp phương trình có 4 nghiệm thì tổng các nghiệm luôn bằng 0 và tích các nghiệm sẽ bằng c/a.

Giải phương trình bậc 4 bằng cách đặt ẩn phụ

Bài tập vận dụng

1. Giải phương trình trùng phương x^4 - 5^2 + 4 = 0

Ta đặt t = x^2 với điều kiện t >= 0

Khi đó phương trình x^4 - 5^2 + 4 = 0 trở thành t^2 - 5t + 4 = 0 (1)

Giải phương trình (1) ta có: a = 1; b = -5; c = 4 => a + b + c = 0

=> Phương trình (1) có 2 nghiệm t1 = 1 và t2 = c/a = 4. Cả 2 nghiệm này đều thỏa mãn điều kiện.

• Với t = 1 => x^2 = 1 => x = 1 hoặc x = -1

• Với t = 4 => x ^2 = 4 => x = 2 hoặc x = -2

Kết luận phương trình x^4 - 5^2 + 4 = 0 có tập nghiệm là S = {-2; -1; 1; 2}

2. Giải phương trình trùng phương 2x^4 - 3x^2 - 2 = 0

Ta đặt t = x^2 với điều kiện t > = 0

Khi đó phương trình 2x^4 - 3x^2 - 2 = 0 sẽ trở thành 2t^2 - 3t - 2 = 0 (2)

Giải phương trình (2) ta được a = 2, b = -3, c = -2 => Δ = (-3)^2 - 4.2.(-2) = 25 > 0

=> Phương trình (2) có 2 nghiệm là t1 = (3 + √25) / 2.2 = (3 + 5)/4 = 2

t2 = (3 - √25) / 2.2 = (3 - 5)/ 4 = -½

Đối chiếu với điều kiện ta thấy chỉ có t1 = 2 thỏa mãn điều kiện t >= 0

Như vậy với t = 2 => x^2 = 2 => x = √2 hoặc x = -√2

Kết luận phương trình 2x^4 - 3x^2 - 2 = 0 có tập nghiệm là S = {-√2; √2}.

Phương pháp giải phương trình trùng phương đưa về giải phương trình tích

Bên cạnh phương pháp đặt ẩn phụ thì chúng ta có thể giải phương trình bậc 4 có dạng ax^4 + b^2 + c = 0 bằng cách đưa về giải phương trình tích.

Cách thực hiện

Đối với phương pháp này chúng ta thực hiện biến đổi đưa về dạng phương trình tích: A.B = 0 ⇔ A = 0 hoặc B = 0.

Bài tập vận dụng

Giải phương trình 2x^2 + 1 = 1/x^2 - 4

Điều kiện xác định là x khác 0

Tiến hành quy đồng, khử mẫu ta được:

2x^2 + 1 = 1/x^2 - 4 ⇔ 2x^4 + x^2 = 1 - 4x^2

⇔ 2x^4 + x^2 + 4x^2 - 1 = 0

⇔ 2x^4 + 5x^2 - 1 = 0 (1)

Đặt t = x^2 với điều kiện t > 0 (vì x khác 0)

Khi đó phương trình (1) có dạng 2t^2 + 5t - 1 = 0 (2)

Giải phương trình (2) ta được: a = 2, b = 5, c = -1 => Δ = 5^2 - 4.2.(-1) = 33 > 0

Như vậy phương trình (2) có 2 nghiệm phân biệt là t1 = (-5 + √33) / 4;

t2 = (-5 - √33) / 4

Đối chiếu với điều kiện t > 0 chỉ có t1 thỏa mãn nên:

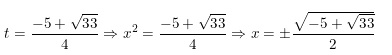
Kết luận phương trình có tập nghiệm là:

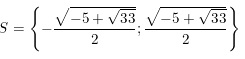
Tổng kết

Trên đây là phần lý thuyết cơ bản và phương pháp giải phương trình trùng phương cùng các bài tập vận dụng mà thayphu.net chia sẻ. Chúc các em áp dụng thành công, hoàn thành tốt mọi dạng bài và đạt điểm cao trong các kỳ thi!