Phương pháp tìm x để P nguyên và bài tập vận dụng chi tiết

Các phương pháp tìm x để biểu thức là một số nguyên. Các bài tập vận dụng về dạng toán này từ cơ bản đến nâng cao để luyện thi vào 10.

Tìm x để p nguyên là một dạng bài toán phổ biến trong toán học, đặc biệt là chương trình toán lớp 9 và các đề ôn luyện thi vào lớp 10. Nó yêu cầu tìm giá trị của x sao cho biểu thức p đã cho là một số nguyên.

Trong bài viết dưới đây, thayphu sẽ cùng các bạn tìm hiểu về các phương pháp để giải dạng bài toán "Tìm x để p nguyên" và áp dụng nó vào các ví dụ cụ thể và bài tập vận dụng nhé.

Các phương pháp tìm x để p nguyên

Cách 1: Chuyển biểu thức sang dạng phân số với tử số là số nguyên, tìm giá trị của biến sao cho mẫu số là ước của tử số.

• Bước 1: Chuyển biểu thức sang dạng

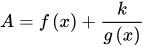
Trong đó f(x) là biểu thức số nguyên khi x là số nguyên và k là giá trị số nguyên.

• Bước 2: Sử dụng điều kiện và bất đẳng thức đã cho chứng minh m < A < M, trong đó m, M là số nguyên.
• Bước 3: Tìm giá trị nguyên trong khoảng từ m đến M.
• Bước 4: Với mỗi giá trị nguyên, tìm giá trị của biến x
• Bước 5: Kết hợp các điều kiện kiểm tra, loại bỏ các giá trị không phù hợp và rút ra kết luận.

Cách 2: Đánh giá phạm vi giá trị của biểu thức và rút ra giá trị nguyên mà biểu thức có thể đạt tới trong phạm vi đó.

• Bước 1: Thiết lập điều kiện trên x sao cho biểu thức A có nghĩa.
• Bước 2: Rút gọn biểu thức A.
• Bước 3: Đánh giá phạm vi giá trị mà biểu thức A có thể đạt tới và từ phạm vi giá trị này ta thu được các giá trị nguyên mà biểu thức A có thể đạt tới.
• Bước 4: Giải phương trình, vế trái là biểu thức rút gọn A, vế phải là giá trị nguyên trong khoảng A. So sánh điều kiện và kết luận.

Cách 3: Thiết lập biểu thức với tham số nguyên và tìm khoảng giá trị của tham số, từ khoảng giá trị này ta xét giá trị nguyên của tham số và giải tìm lớp ẩn.

• Bước 1: Thiết lập điều kiện trên x sao cho biểu thức A có nghĩa
• Bước 2: Rút gọn biểu thức A
• Bước 3: Đánh giá phạm vi giá trị mà biểu thức A có thể đạt tới, từ phạm vi giá trị này ta thu được các giá trị nguyên mà biểu thức A có thể đạt tới.
• Bước 4: Giải phương trình, vế trái là biểu thức rút gọn A, vế phải là giá trị nguyên trong khoảng A. So sánh điều kiện và kết luận.

Bài tập vận dụng từ cơ bản đến nâng cao

Bài 1: Tính giá trị nguyên của x để biểu thức sau mang giá trị nguyên.

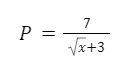
Gợi ý lời giải:

ĐKXĐ: x > 0

Muốn biểu thức P nhận giá trị nguyên thì √x + 3 ∈ U(7) = {±1; ±7}

Từ đó ta có thể suy ra: x ≥ 0 → √x + 3 ≥ 3

→ √x + 3 = 7

→ √x = 4 → x = 16 (thỏa mãn điều kiện)

Vậy để biểu thức P mang giá trị nguyên thì x = 16.

Bài 2: Cho hai biểu thức A, B như sau:

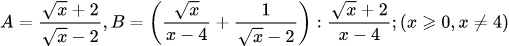
a) Rút gọn biểu thức B

b) Tìm các giá trị nguyên của x để biểu thức P = A(B - 2) đạt giá trị nguyên.

Gợi ý lời giải:

1. ĐKXĐ: x ≥ 0, x ≠ 4

Rút gọn biểu thức B ta được:

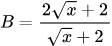
2. Ta có: P = A(B - 2) = -2 / (√x - 2)

Muốn biểu thức P có giá trị nguyên tức là -2 / (√x - 2) phải mang giá trị nguyên.

→ √x - 2 ∈ U(2) → √x - 2 ∈{±1; ±2}

Biết rằng muốn x là một số nguyên thì có 2 trường hợp.

• √x là số nguyên ( nếu x là một số chính phương).

• √x là số vô tỉ ( nếu x là một số không chính phương).

Để biểu thức là một số nguyên thì √x không thể là số vô tỉ → √x là số nguyên.

Ta kẻ một bảng giá trị như sau:

Vậy để biểu thức A đạt giá trị nguyên thì x ∈ { 1; 3; 16}.

Bài 3: Cho biểu thức:

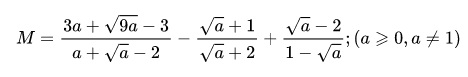
1. Hãy rút gọn biểu thức M.

2. Tìm tất cả các giá trị nguyên của a để M mang giá trị nguyên.

Gợi ý lời giải:

1. Từ biểu thức M đã cho, ta có:

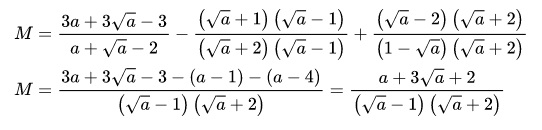
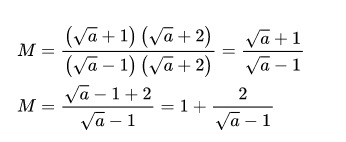
2. Từ biểu thức M rút gọn, ta có thể suy ra biểu thức M mang giá trị nguyên khi và chỉ khi 2/(√a - 1) nguyên.

→ √a - 1 ∈ U(2) = {-1; 1; 2}

→ a ∈ {0; 4; 9}

Vậy để biểu thức M mang giá trị nguyên thì a = 0; 4; 9.

Kết luận

Việc giải các dạng bài toán tìm x để p nguyên không chỉ giúp chúng ta hiểu sâu hơn về tính chất của các số nguyên, mà còn áp dụng rộng rãi trong nhiều lĩnh vực toán học và khoa học khác nhau.

Qua bài viết trên, thayphu hy vọng các bạn đã hiểu rõ các phương pháp để giải dạng toán tìm x để biểu thức P nguyên. Đồng thời vận dụng và ôn luyện chúng thật nhiều, thật tốt để giải các dạng bài tập ôn luyện từ cơ bản đến nâng cao, đặc biệt là các bài toán thường xuyên ra trong đề thi vào lớp 10. Bởi lẽ, đây là một trong những kiến thức trọng tâm và rất quan trọng trong chương trình toán lớp 9, là nền tảng cơ bản để giải được những bài toán ở cấp cao hơn và phức tạp hơn.