Tiên đề Euclid về đường thẳng song song và các bài tập

Nội dung tiên đề Euclid về đường thẳng song song là gì? Các dạng bài tập liên quan có kèm cách giải chi tiết, đơn giản và dễ hiểu giúp các em dễ dàng thực hành.

Tổng hợp lý thuyết về tiên đề Euclid cùng các bài tập tiên đề Euclid về đường thẳng song song Toán lớp 7 có chọn lọc kèm đáp án. Bài viết này thayphu sẽ cùng các em hệ thống lại kiến thức và ôn luyện để hoàn thành tốt nội dung này nhé!

Tiên đề Euclid về đường thẳng song song

Tiên đề Euclid về đường thẳng song song

Tiên đề Euclid: Qua 1 điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

Ví dụ minh họa: Cho điểm M nằm ngoài đường thẳng a thì b đi qua M và song song với a là duy nhất.

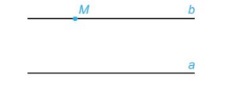
Lưu ý: Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại.

Ví dụ minh họa: Cho hai đường thẳng song song với nhau là a và b. Nếu đường thẳng c cắt đường thẳng a thì cũng cắt đường thẳng b.

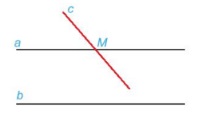
Bài tập về tiên đề Euclid

Bài tập 1

Cho tam giác ABC, vẽ đường thẳng m đi qua A và song song với BC. Vẽ đường thẳng n đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng m, bao nhiêu đường thẳng n? Vì sao?

Cách giải:

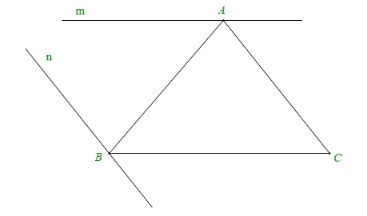
Theo tiên đề Euclid, qua điểm A ở ngoài BC, chỉ có một đường thẳng song song với BC. Do đó chỉ vẽ được một đường thẳng m duy nhất.

Theo tiên đề Euclid, qua điểm B ở ngoài AC chỉ có một đường thẳng song song với AC. Do đó chỉ vẽ được một đường thẳng n duy nhất.

Bài tập 2

Cho hình vẽ, biết mn // ab và xHm = 120 độ. Hãy tính các góc còn lại trong hình vẽ dưới đây:

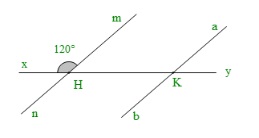
Cách giải:

Ta có: nHy = xHm (2 góc đối đỉnh)

=> nHy = 120 độ

Ta có: xHm + xHn = 180 độ (2 góc kề bù)

Thay số: 120 độ + xHn = 180 độ

=> xHn = 180 độ - 120 độ

=> xHn = 60 độ

Ta có: mHy = xHn = 60 độ (2 góc đối đỉnh)

Vì mn // ab nên:

xKb = mHy (2 góc so le trong) => xKb = 60 độ

xKa = xHm (2 góc đồng vị) => xKa = 120 độ

aKy = mHy (2 góc đồng vị) => aKy = 60 độ

bKy = nHy (2 góc đồng vị) => bKy = 120 độ

Kết luận: nHy = 120 độ; xHn = 60 độ; mHy = 60 độ; xKb = 60 độ; xKa = 120 độ; aKy = 60 độ; bKy = 120 độ.

Bài tập 3

Cho hình dưới đây, hãy giải thích tại sao

1. a song song với b
2. b vuông góc với d

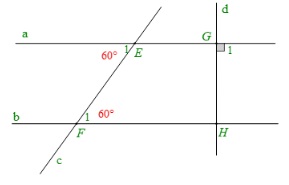
Cách giải:

1. Ta có: E1 = F1 = 60 độ

Mà 2 góc này ở vị trí so le trong.

Vì vậy a // b (theo dấu hiệu nhận biết 2 đường thẳng song song)

2. Ta có: G1 = 90 độ nên d a

Mà theo câu a thì a // b

Vì vậy d b (theo tính chất của 2 đường thẳng song song)

Bài tập 4

Cho hình dưới đây

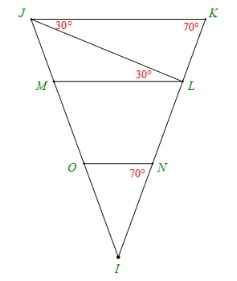
Hãy giải thích tại sao

1. JK // ML
2. JK // ON
3. MN // ON

Cách giải:

1. Ta có: KJL = JLM = 30 độ

Mà 2 góc ở vị trí so le trong

Do đó JK // ML (dấu hiệu nhận biết 2 đường thẳng song song).

2. Ta có: JKL = ONI = 70 ĐỘ

Mà 2 góc ở vị trí đồng vị

Do đó JK // ON (dấu hiệu nhận biết 2 đường thẳng song song)

3. Ta có: JK // ML (theo câu a) và JK // ON (theo câu b)

=> MN // ON (dựa theo tính chất 2 đường thẳng song song).

Bài tập 5

Cho hình vẽ dưới đây, biết a // b, hãy tính tổng A1 + B4

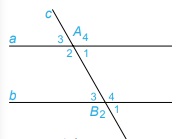
Cách giải:

Ta có A1 và B3 là 2 góc so le trong mà a // b nên A1 = B3 (tính chất 2 đường thẳng song song)

B3 và B4 là 2 góc kề bù nên B3 + B4 = 180 độ

=> A1 + B4 = 180 độ

Bài tập 6

Cho hình vẽ dưới đây

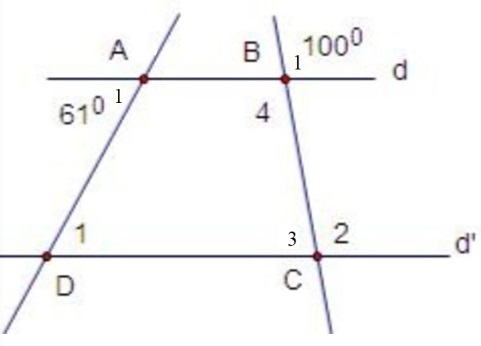
Biết d // d’ hãy xác định khẳng định nào sau đây là sai?

1. D1 = 61 độ
2. B4 = 100 độ
3. C3 = 80 độ
4. C2 = 110 độ

Cách giải:

Ta có d // d’ mà A1 và D1 nằm ở vị trí so le trong

Nên A1 = D1 = 61 độ (tính chất 2 đường thẳng song song)

=> Khẳng định A đúng

Tiếp đó: B4 và B1 là 2 góc đối đỉnh

Nên B4 = B1 = 100 độ

=> Khẳng định B đúng

Vì d // d’ mà B4 và C3 ở vị trí trong cùng phía

Nên B4 + C3 = 180 độ => C3 = 180 độ - 100 độ = 80 độ

=> Khẳng định C đúng.

Kết luận khẳng định sai là D.

Bài tập 7

Hãy xác định có bao nhiêu cặp đường thẳng song song trong hình vẽ sau đây?

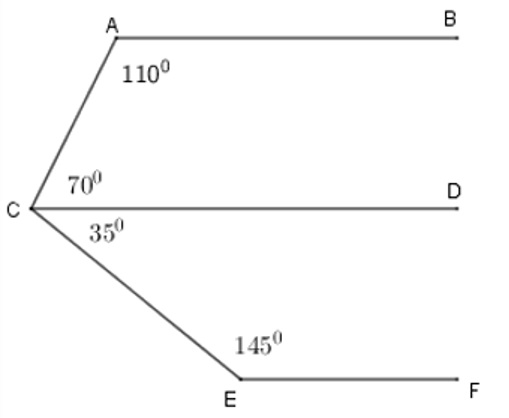
Cách giải:

Ta có:

BAC và ACD ở vị trí trong cùng phía và BAC + ACD = 110 độ + 70 độ = 180 độ

=> AB // CD (dấu hiệu nhận biết 2 đường thẳng song song)

Bên cạnh đó:

DCE và CEF ở vị trí trong cùng phía và DCE + CEF = 35 độ + 145 độ = 180 độ

=> EF // CD (dấu hiệu nhận biết 2 đường thẳng song song)

Ta lại có:

AB // CD và EF // CD => AB // EF

Như vậy có 3 cặp đường thẳng song song trong hình vẽ.

Bài tập 8

Cho hình vẽ sau đây

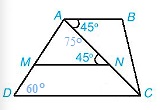
Khẳng định nào sau đây là sai?

1. MN // DC
2. AB // DC
3. AMN = 60 độ
4. ACD = 60 độ

Cách giải:

• Ta có:

BAC = ANM = 45 độ

Mà 2 góc này so le trong nên AB // MN

Do đó khẳng định A là đúng.

• Xét tam giác AMN ta có:

MAN + AMN + ANM = 180 độ

=> AMN = 180 độ - (MAN + ANM) = 180 độ - (75 độ + 45 độ) = 60 độ

Ta lại có:

AMN= ADC = 60 độ

Mà 2 góc này là 2 góc đồng vị nên MN // DC

Do đó B, C đúng

=> ANM = ACD = 45 độ

Kết luận khẳng định C và D là sai.

Trên đây bài viết vừa tổng hợp về nội dung của tiên đề Euclid và các bài tập vận dụng kèm lời giải. Các em hãy cùng thực hành để nắm vững kiến thức này. Đừng quên theo dõi kênh thường xuyên để cập nhật các bài học mới nhất từ thayphu nhé!