Kiến thức phương trình mặt cầu kèm bài tập áp dụng có đáp án

Tìm hiểu về kiến thức phương trình mặt cầu kèm theo một số dạng bài tập liên quan quan đến phương trình mặt cầu này tại đây.

Phương trình mặt cầu trong không gian - dạng toán hình học đang được giảng dạy trong chương trình học của học sinh lớp 12. Các kiến thức liên quan đến hình học tương đối khó với người học, đòi hỏi tư duy logic và khả năng tiếp thu kiến thức hình học đã được giảng dạy mới có thể giải được các dạng bài tập liên quan.

Bài viết dưới đây của thayphut.net là những thông tin chi tiết về dạng toán này kèm theo một vài bài tập áp dụng có đáp án.

Lý thuyết và công thức phương trình mặt cầu

Để giải được các bài tập liên quan đến phương trình mặt cầu, bạn cần nắm được lý thuyết của phương trình mặt cầu thông qua nội dung sau:

Phương trình mặt cầu là gì?

Trước khi tìm hiểu kiến thức về phương trình mặt cầu, vậy bạn đã biết mặt cầu là gì chưa? Mặt cầu là quỹ tích các điểm cách đều điểm đã cho trước một khoảng không đổi, với khoảng không đổi đó gọi là bán kính và điểm cho trước là tâm mặt cầu.

Phương trình mặt cầu gồm có 2 dạng chính là phương trình chính tắc và phương trình tổng quát:

Công thức phương trình mặt cầu chính tắc và tổng quát

Phương trình mặt cầu là kiến thức bắt buộc học sinh phải hiểu và áp dụng được trong bài tập hình học liên quan. Các kỳ thi hoặc kiểm tra như 15 phút, 1 tiết, giữa học kì, học kỳ, tốt nghiệp THPT, tuyển sinh đại học đều có một số bài tập liên quan đến kiến thức hình học phương trình mặt cầu. Phương trình hình học tuy khó đòi hỏi người học phải bỏ ra nhiều thời gian để tiếp thu, học hình học giúp học sinh rèn luyện được khả năng logic và tư duy phân tích giải quyết tình huống sau này.

Xác định vị trí tương đối giữa mặt phẳng và mặt cầu

Mặt cầu (S): (x−a)2 + (b−y)2 + (c−z)2 = R2 với tâm I, bán kính R và mặt phẳng (P): Ax+By+Cz+D=0.

• Trường hợp d(I,(P)) > R thì mặt phẳng (P) không cắt mặt cầu (S).

• Trường hợp d(I,(P)) = R thì mặt phẳng (P) tiếp xúc với mặt cầu (S).

• Trường hợp d(I,(P)) < R thì mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến xác định là đường tròn có tâm K, là hình chiếu của I trên (P) và bán kính r=√R2−d2(I,(P)).

Xác định vị trí tương đối giữa đường thẳng và mặt cầu

Mặt cầu (S): (x−a)2 + (b−y)2 + (c−z)2 = R2 với tâm I, bán kính R và đường thẳng Δ, d là khoảng cách từ mặt cầu (S) đến đường thẳng Δ:

• Trường hợp d > R thì đường thẳng Δ không cắt mặt cầu (S).

• Trường hợp d = R thì đường thẳng Δ tiếp xúc với mặt cầu (S).

• Trường hợp d < R thì đường thẳng Δ cắt mặt cầu (S) theo dây cung AB = √R2 – d2.

Bài tập có đáp án về phương trình mặt cầu

Bài tập về phương trình mặt cầu sẽ có 6 dạng chính, tuy nhiên trong bài viết dưới đây sẽ chia sẻ về 3 dạng bài tập có đáp án về phương trình mặt cầu cơ bản nhất. Học sinh chỉ cần đọc sơ qua cách giải 3 dạng cơ bản dưới đây đã có thể nắm được lý thuyết và hiểu được phương trình mặt cầu.

Dạng 1: Tìm tọa độ tâm I và bán kính R của phương trình mặt cầu cho sẵn

Bài tập:

Cho mặt cầu (S) có phương trình là x2 + y2 +z2 + 2x – 4y + 6z – 2= 0 . Xác định tọa độ tâm I và bán kính R của (S).

Bài giải:

Phương trình mặt cầu tổng hợp là (x−a)2 + (b−y)2 + (c−z)2 = R2

=> x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0.

=> Tâm I (-1, 2, 3)

R = √a2 + b2 + c2 – d = √(-1)2 + (2)2 + (3)2 – (-2) = √16 = 4

Dạng 2: Viết phương trình mặt cầu khi cho sẵn biết tâm và bán kính

Bài tập

Cho mặt cầu có tâm I (2; 2; -3) và bán kính R = 3, hãy viết phương trình mặt cầu có tâm I và bán kính R này.

Bài giải:

Phương trình mặt cầu tổng hợp là (x−a)2 + (y -b)2 + (z - c)2 = R2

Với tâm I (a; b; c) => Phương trình mặt cầu là: ( x - 2)2 + ( y - 2)2 + ( z + 3)2 = 9

Dạng 3: Viết phương trình mặt cầu khi cho sẵn đường kính

Bài tập:

AB là đường kính của mặt cầu tâm M là A( -2; 1; 0) / B( 2;3 ; -2), tâm M chính là tâm điểm của mặt cầu cần tìm, có đường kính R = MA. Xác định phương trình mặt cầu có đường kính AB trên.

Bài giải:

Tọa độ của tâm M được xác định như sau:

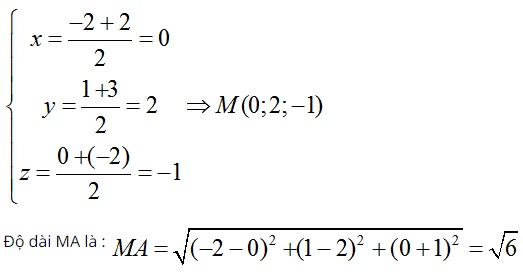
Tâm M(0; 2; -1) và có bán kính là R = MA = MB = √6

Ta có phương trình mặt cầu như sau: (x – 0)2 + ( y – 2)2 + ( z+ 1)2 = 6

Trên đây là 3 dạng toán hình học phương trình mặt cầu cơ bản nhất trong tổng 6 dạng bài tập kèm lời giải chi tiết. Tham khảo để nắm được các dạng toán cơ bản này và cách giải đã được hướng dẫn.

Kết luận

Bài viết trên đã chia sẻ chi tiết về lý thuyết liên quan đến phương trình mặt cầu kèm theo một vài dạng bài tập kèm đáp án về phương trình để bạn tham khảo. Hy vọng thông qua bài viết, bạn sẽ nắm được dạng toán hình học này và hiểu được cách giải dạng toán cơ bản của dạng bài tập phương trình mặt cầu.