Hiểu kiến thức về hình lăng trụ tam giác đều trong 5 phút

Tìm hiểu về định nghĩa, tính chất và các công thức cần phải nhớ về hình lăng trụ tam giác đều. Cùng với đó là 1 số bài tập vận dụng để nhớ kiến thức

Lăng trụ tam giác đều thuộc về kiến thức lớp 12 khối THPT. Đây là một dạng bài thường xuyên xuất hiện trong các đề thi tốt nghiệp quốc gia của Bộ GDĐT. Rõ ràng nhu cầu tìm hiểu về hình lăng trụ tam giác đều là rất lớn.

Chúng ta cần hiểu rõ để tránh nhầm lẫn với hình lăng trụ có đáy là tam giác đều. Do đó bài viết này của thayphu.net sẽ giúp bạn đọc hiểu kiến thức về hình lăng trụ tam giác đều trong 5 phút.

Hình lăng trụ tam giác đều là gì?

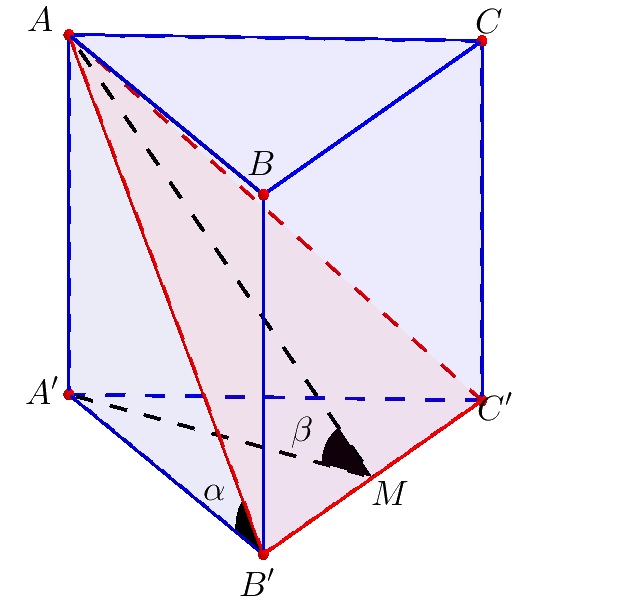
Hình lăng trụ tam giác đều.

Định nghĩa: Hình lăng trụ tam giác đều là một đa diện có 2 đáy là 2 tam giác đều bằng nhau nằm trên 2 mặt phẳng song song, các mặt bên là hình chữ nhật, các cạnh bên song song và bằng nhau, vuông góc với mặt đáy.

Với định nghĩa như vậy thì đa giác đều sẽ có các tính chất sau đây. Bạn cần nắm rõ các tính chất này để giải quyết các câu hỏi và bài tập.

· Hai đáy là 2 tam giác đều bằng nhau

· Chiều cao lăng trụ tam giác đều là độ dài của cạnh bên

· Các mặt bên là các hình chữ nhật bằng nhau

· Các mặt bên và hai đáy vuông góc với nhau.

· α: là góc giữa đường chéo của mặt bên và đáy (trong lăng trụ tam giác đều các đường chéo mặt bên tạo với đáy các góc bằng nhau).

· β: là góc giữa hai mặt phẳng (AB’C) và đáy (A’B’C’)

Các công thức tính lăng trụ tam giác cần phải nhớ

Tính thể tích hình lăng trụ tam giác đều

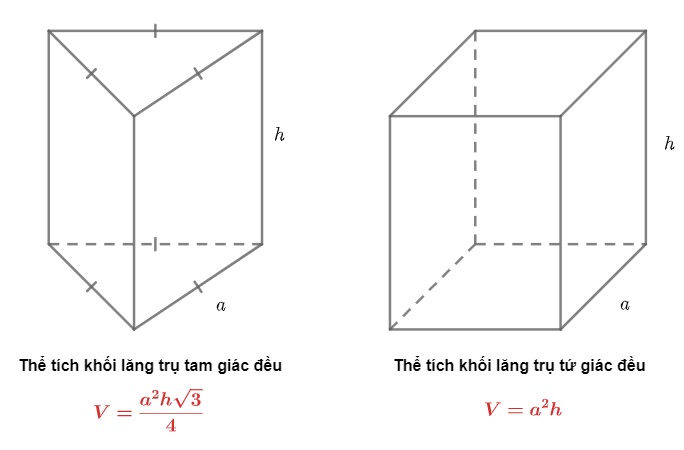
Công thức tính lăng trụ tam giác.

Thể tích hình lăng trụ tam giác đều cũng như các hình lăng trụ khác sẽ bằng diện tích mặt đáy nhân với chiều cao của hình lăng trụ

V = S x h = a2 x √3/4 x h

Trong đó:

· V: Thể tích hình lăng trụ tam giác đều

· S: Diện tích đáy tam giác đều

· h: Chiều cao của hình lăng trụ (đọ dài cạnh bên)

· a: Độ dài của cạnh tam giác đều

Có thể thấy trong công thức trên thì ngoài h là chiều cao của hình lăng trụ tam giác đều thì S sẽ có cách tính từ độ dài cạnh của tam giác đều cạnh bằng a: Sđ = a2 x (√3)/4

Tính diện tích xung quanh hình lăng trụ tam giác đều

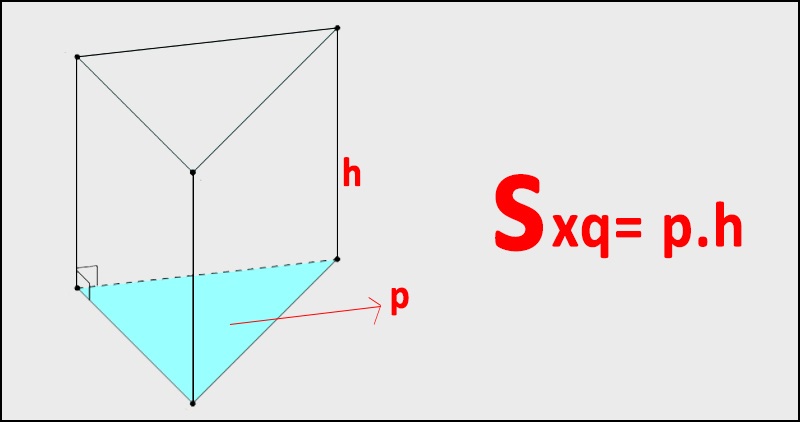
Tính diện tích xung quanh hình lăng trụ tam giác đều.

Diện tích xung quanh hình lăng trụ tam giác đều bằng tổng diện tích các mặt bên tức là diện tích của 3 hình chữ nhật. Mà diện tích hình chữ nhật sẽ bằng cạnh đánh nhân với chiều cao. Điều đó đồng nghĩa diện tích xung quanh = chu vi đáy x chiều cao.

S­xq = a x h + a x h + a x h = 3 x a x h = P x h

Trong đó:

S­xq : Diện tích xung quanh hình lăng trụ tam giác đều

a: Độ dài cạnh tam giác đều

h: Chiều cao hình lăng trụ tam giác đều

P: Chu vi tam giác đều

Tính diện tích toàn phần hình lăng trụ tam giác đều

Diện tích toàn phần hình lăng trụ tam giác đều bằng tổng diện tích các mặt bên và diện tích của 2 đáy tam giác đều. Mà diện tích các mặt bên chính là diện tích xung quanh.

Stp = Sxq + 2 x Sđ = 3 x a x h + 2 x (√3)/4 x a2

Trong đó:

Stp: Diện tích toàn phần hình lăng trụ tam giác đều

Sxq: Diện tích xung quanh hình lăng trụ tam giác đều

Sđ: Diện tích đáy hình lăng trụ tam giác đều

a: Độ dài cạnh tam giác đều

h: Chiều cao hình lăng trụ tam giác đều

Một số bài tập về lăng trụ tam giác đều vận dụng

Câu 1. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 5. Thể tích khối lăng trụ đã cho bằng bao nhiêu?

Đáp án:

Áp dụng công thức: V = a2 x √3/4 x h

Khi đề bài cho tất cả các cạnh bằng 3 thì đồng nghĩa chiều cao h cũng bằng 3. Nên nhớ trong tính chất của hình lăng trụ tam giác đều thì Chiều cao lăng trụ là độ dài của cạnh bên

Do đó Thể tích: V = 52 x √3/4 x 5 = (125√3)/4

Câu 2: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC đều cạnh bằng a và chu vi của mặt bên ABB’A’ bằng 6a . Thể tích của khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?

Đáp án:

Chúng ta cần hiểu rằng đề bài này cần thêm chiều cao h sẽ tính được thể tích V.

Do chu vi của mặt bên ABB’A’ bằng 6a nên theo tính chất hình lăng trụ tam giác đều ta có:

2 x (a + h) = 6a → h = 2a

Vậy áp dụng công thức thể tích V = a2 x √3/4 x h = a3 x √3/2

Câu 3: Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 5. Diện tích xung quanh lăng trụ đã cho bằng bao nhiêu?

Đáp án:

Áp dụng công thức: Stp = Sxq + 2 x Sđ = 3 x a x h + 2 x (√3)/4 x a2

Ở đây khi các cạnh bằng 5 thì chiều cao h = 5.

Do đó Stp = 3 x a2 + 2 x (√3)/4 x a2 = (3 + 2(√3)/4) x a2

Lời kết hiểu kiến thức về hình lăng trụ tam giác đều trong 5 phút

Rõ ràng kiến thức lăng trụ tam giác đều không quá phức tạp. Nó chỉ là một phần kiến thức nhỏ trong khối lượng kiến thức hình học lớp 12 mà thôi. Do đó bạn cần phải nắm thật chắc nó để không bị bỏ lỡ những điểm số cần thiết ở các kỳ thi quan trọng của cuộc đời mình sắp tới. Đừng quên ghé thăm trang web thayphu.net để học hỏi thêm nhiều kiến môn toán nhé! Chúc bạn thành công!