Hiểu kiến thức về hình lăng trụ tứ giác đều trong 5 phút
Tìm hiểu về định nghĩa, tính chất và các công thức cần phải nhớ về hình lăng trụ tứ giác đều. Cùng với đó là 1 số bài tập vận dụng để nhớ kiến thức.
Hình lăng trụ tứ giác đều là kiến thức hình học lớp 12. Do đó nó hay xuất hiện trong các đề thi tốt nghiệp quốc gia. Hơn nữa đây cũng là vật mà chúng ta có thể thấy ngoài thực tế khá nhiều. Nó được áp dụng trong xây dựng, thiết kế nội thất, thiết kế trang trí,… và rất nhiều lĩnh vực khác.
Rõ ràng kiến thức về Hình lăng trụ tứ giác đều là rất cần thiết, bài viết sau đây của thayphu.net sẽ giúp bạn đọc Hiểu kiến thức về hình lăng trụ tứ giác đều trong 5 phút
Hình lăng trụ tứ giác đều là gì
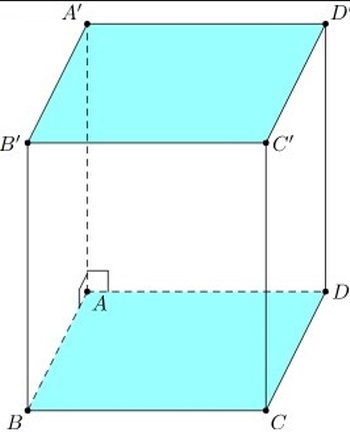
Định nghĩa: Hình lăng trụ tứ giác đều là một đa diện có 2 đáy là 2 hình vuông bằng nhau nằm trên 2 mặt phẳng song song, các mặt bên là hình chữ nhật, các cạnh bên song song và bằng nhau, vuông góc với mặt đáy. Đây được xem là hình hộp chữ nhật có 2 đáy là hình vuông.
Với định nghĩa như vậy thì Hình lăng trụ tứ giác đều sẽ có các tính chất sau đây. Bạn đọc cần nắm rõ các tính chất này để giải quyết các bài tập liên quan tới nó:
- Hai đáy là 2 hình vuông bằng nhau
- Chiều cao lăng trụ tứ giác đều là độ dài của cạnh bên
- Các mặt bên là các hình chữ nhật bằng nhau
- Các mặt bên và hai đáy vuông góc với nhau.
Các công thức tính cần phải nhớ
Tính thể tích hình lăng trụ tứ giác đều
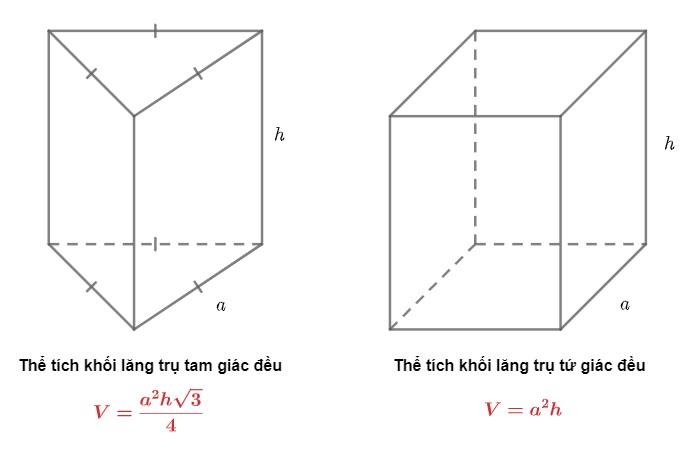
Thể tích hình lăng trụ tứ giác đều cũng như các hình lăng trụ khác sẽ bằng diện tích mặt đáy nhân với chiều cao của hình lăng trụ
V = S x h = a2 x h
Trong đó:
· V: Thể tích hình lăng trụ tứ giác đều
· S: Diện dích đáy tứ giác đều
· h: Chiều cao của hình lăng trụ chính là độ dài cạnh bên
· a: Độ dài của cạnh tứ giác đều (hình vuông)
Có thể thấy trong công thức trên thì ngoài h là chiều cao của hình lăng trụ tam giác đều thì S sẽ có cách tính từ độ dài cạnh của tứ giác đều cạnh bằng a: Sđ = a2.
Tính diện tích xung quanh hình lăng trụ tứ giác đều
Diện tích xung quanh hình lăng trụ tam giác đều bằng tổng diện tích các mặt bên tức là diện tích của 4 hình chữ nhật. Mà diện tích hình chữ nhật sẽ bằng cạnh đánh nhân với chiều cao. Điều đó đồng nghĩa diện tích xung quanh = chu vi đáy x chiều cao.
Sxq = a x h + a x h + a x h + a x h= 4 x a x h = P x h
Trong đó:
Sxq : Diện tích xung quanh hình lăng trụ tứ giác đều
a: Độ dài cạnh tứ giác đều
h: Chiều cao hình lăng trụ tứ giác đều
P: Chu vi tứ giác đều
Tính diện tích toàn phần hình lăng trụ tứ giác đều
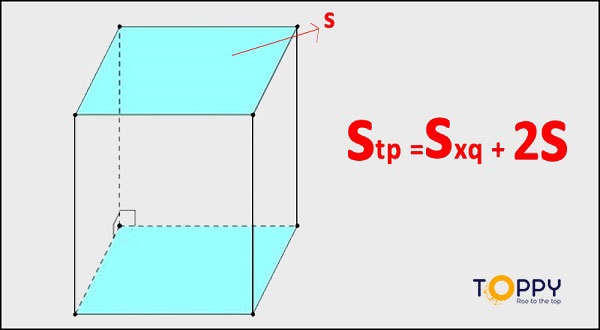
Diện tích toàn phần hình lăng trụ tứ giác đều bằng tổng diện tích các mặt bên và diện tích của 2 đáy tứ giác đều. Mà diện tích các mặt bên chính là diện tích xung quanh chúng ta đã tính ở trên.
Stp = Sxq + 2 x Sđ = 4 x a x h + 2 x a2
Trong đó:
Stp: Diện tích toàn phần hình lăng trụ tứ giác đều
Sxq: Diện tích xung quanh hình lăng trụ tứ giác đều
Sđ: Diện tích đáy hình lăng trụ tứ giác đều
a: Độ dài cạnh tứ giác đều
h: Chiều cao hình lăng trụ tứ giác đều
Một số bài tập vận dụng về kiến thức hình lăng trụ tứ giác đều
Câu 1. Lăng trụ tứ giác đều có độ dài cạnh đáy bằng 5, cạnh bên bằng 10. Thể tích khối lăng trụ đã cho bằng bao nhiêu?
Đáp án:
Áp dụng công thức: V = a2 x h
Cạnh bên bằng 10 thì theo tính chất lăng trụ tứ giác đều chiều cao h = 10.
Do đó Thể tích: V = 52 x 10 = 250
Câu 2. Hình lăng trụ tứ giác đều có cạnh đáy bằng 6, diện tích mặt bên bằng 42. Tính thể tích khối lăng trụ đã cho bằng bao nhiêu?
Đáp án:
Do diện tích mặt bên bằng 42. Ta sẽ tính được chiều cao h = 42/6 = 7
Áp dụng công thức: V = a2 x h
Do đó Thể tích: V = 62 x 7 = 252
Câu 3. Cho lăng trụ tứ giác đều có tất cả các cạnh bằng 10. Tính diện tích xung quanh và diện tích toàn phần khối lăng trụ đó?
Đáp án:
Áp dụng công thức: Sxq = 4 x a x h và Stp = Sxq + 2 x Sđ
Do đó Diện tích xung quanh: Sxq = 4 x 10 x 10 = 400
Diện tích toàn phần: Stp = 400 + 2 x 102 = 600
Lời kết Hiểu kiến thức về hình lăng trụ tứ giác đều
Bài viết trên đây cung cấp các thông tin cơ bản về kiến thức hình lăng trụ tứ giác đều. Đây là những kiến thức nền tảng cần phải nắm chắc, các bài tập cũng chỉ ở mức giúp các bạn nắm rõ công thức. Nhưng nó sẽ là cơ sở để bạn đọc có những bước tìm hiểu sâu hơn về hình lăng trụ tứ giác đều. Nên nhớ đây là kiến thức rất hay ra ở đề thi tốt nghiệp quốc gia, một kỳ thi mang tính chất bước ngoặt của cuộc đời. Hãy ghé thăm web thayphu.net để có nhiều kiến thức về môn toán nhé các bạn!


 Định nghĩa góc giữa hai đường thẳng
Định nghĩa góc giữa hai đường thẳng  Góc giữa hai vectơ
Góc giữa hai vectơ 