Lý thuyết công thức số phức và bài tập áp dụng cơ bản

Học nhanh lý thuyế và công thức số phức sẽ giúp giải toán dễ dàng hơn, cũng như áp dụng thêm các bài toán số phức đặc biệt để nâng cao kiến thức.

Khi lên đến trung học phổ thông bạn sẽ được tiếp xúc với nhiều kiến thức mới, trong đó có số phức. Số phức đóng vai trò quan trọng trong nhiều lĩnh vực và việc biết công thức số phức sẽ giúp bạn giải quyết công việc một cách nhanh chóng hơn. Hãy cùng thayphu.net ôn lại kiến thức lớp 12 quan trọng này thông qua bài viết dưới đây nhé.

Số phức là gì? Vai trò của số phức

Tổng hợp công thức số phức

Số phức là một số hữu tỉ được biểu diễn dưới dạng a + bi, trong đó a và b là các số thực, và i là đơn vị ảo thực sự, với i^2 = -1.

Số phức đóng vai trò quan trọng trong nhiều lĩnh vực toán học và khoa học khác nhau, bao gồm cả vật lý, kỹ thuật và công nghệ. Chúng được sử dụng để mô hình hóa các vật thể có tính chất chuyển động, tín hiệu điện, sóng âm thanh và ánh sáng, cũng như trong lý thuyết xác suất và thống kê.

Ngoài ra, số phức cũng được sử dụng trong tính toán và truyền thông điện tử, và là một phần quan trọng trong các phương pháp số học để giải quyết các vấn đề phức tạp trong khoa học và kỹ thuật.

Một số khái niệm liên quan đến số phức:

• Phần thực và phần ảo: Số phức có dạng a + bi, trong đó a là phần thực và b là phần ảo.

• Số phức đối của một số phức z là số phức z̄, có phần thực bằng phần thực của z và phần ảo bằng đối của phần ảo của z.

• Modul của một số phức z là độ dài của vector biểu diễn z trong mặt phẳng phức, được ký hiệu là |z|. Modun của z bằng căn bậc hai của tổng bình phương của phần thực và phần ảo của z: |z| = sqrt(a^2 + b^2). (sqrt là căn bậc 2)

• Số phức thuần ảo là số phức có phần thực bằng 0 và phần ảo khác 0.

Hai số phức bằng nhau khi:

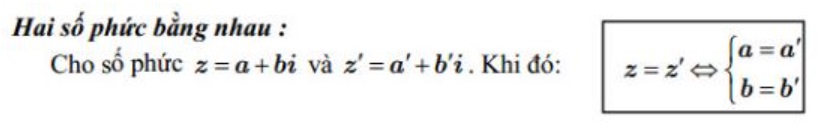
Tổng hợp các công thức số phức mà bạn cần biết

Công thức số phức liên hợp

Số phức của tổng, hiệu, tích thương của 2 số phức sẽ bằng tổng, hiệu, tích thương các liên hợp số phức. Cụ thế ta có thể thấy rõ hơn trong bảng dưới đây:

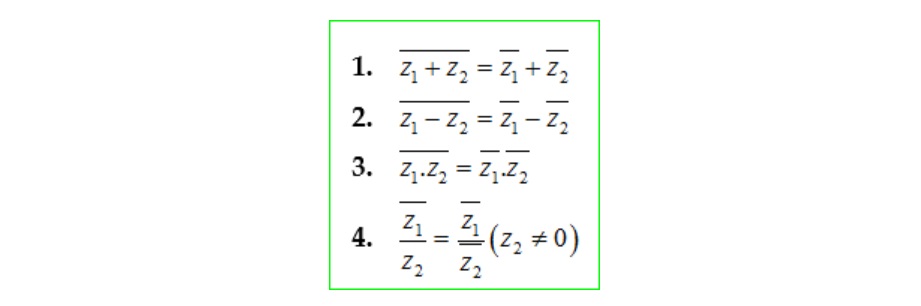
Các công thức mô đun của số phức

Mô đun của tích, thương số phức sẽ bằng tích thương của mô đun 1 và mô đun 2. Cụ thể là:

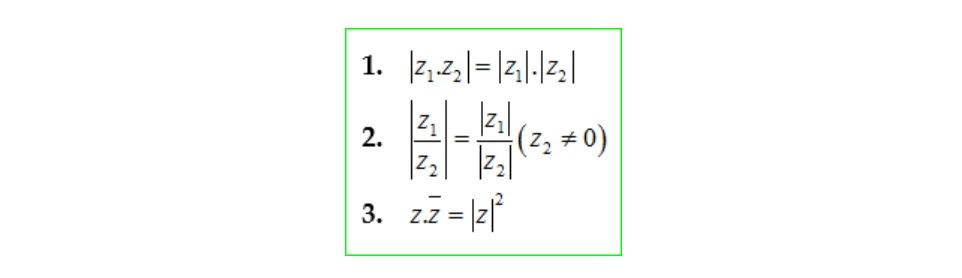
Nhóm công thức bất đẳng thức mô đun số phức

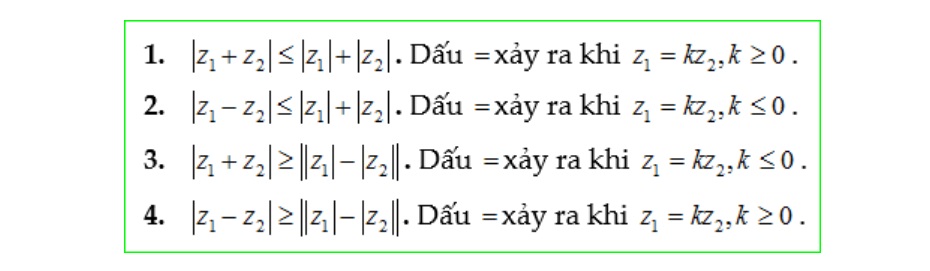
Các tính chất cần nhớ về số phức

Cách tìm căn bậc hai của số phức

Dạng lượng giác của số phức

Dạng lượng giác của số phức là cách biểu diễn số phức dưới dạng tổng của một số phức thực và một số phức ảo, được viết dưới dạng a + bi, với a và b là hai số thực.

Để chuyển từ dạng chung của số phức z = a + bi sang dạng lượng giác, ta có thể sử dụng hai công thức sau:

Phần thực a của số phức z là a = Re(z) = (z + conj(z)) / 2

Phần ảo b của số phức z là b = Im(z) = (z - conj(z)) / (2i)

Trong đó, conj(z) là số phức nghịch đảo của z, tức là conj(z) = a - bi.

Ví dụ, để chuyển số phức z = 2 + 3i sang dạng lượng giác, ta có:

a = (z + conj(z)) / 2 = (2 + 3i + 2 - 3i) / 2 = 2

b = (z - conj(z)) / (2i) = (2 + 3i - 2 + 3i) / (2i) = 3/2

Vậy số phức z = 2 + 3i có dạng lượng giác là 2 + 3/2i.

Đa thức với hệ số phức

Đa thức với hệ số phức là một đa thức mà các hệ số của nó là các số phức. Đa thức với hệ số phức có dạng chung như sau:

P(z) = a_n z^n + a_{n-1} z^{n-1} + ... + a_1 z + a_0

Trong đó, a_n, a_{n-1}, ..., a_1, a_0 là các số phức và z là một biến số phức. Đa thức này có thể được đặt lại dưới dạng tổng của các số phức:

P(z) = (a_n)(z^n) + (a_{n-1})(z^{n-1}) + ... + (a_1)(z) + a_0

Các phép tính toán trên đa thức với hệ số phức tương tự như trên đa thức với hệ số thực, bao gồm tìm các nghiệm, đạo hàm, tích phân, tìm các điểm cực trị và đường cong của đa thức. Đặc biệt, việc tìm nghiệm của đa thức với hệ số phức có thể được thực hiện bằng cách sử dụng các phương pháp như khai căn phức, phương trình đại số đặc trưng và phép giải phương trình bậc hai phức.

Một số dạng bài tập căn bản về số phức

Một số dạng bài tập căn bản về số phức

• Chuyển đổi giữa dạng chung và dạng lượng giác của số phức.

• Tìm độ lớn và góc phần tử của số phức.

• Thực hiện các phép toán cơ bản trên số phức, bao gồm cộng, trừ, nhân, chia và lũy thừa.

• Tìm nghiệm của phương trình hoặc hệ phương trình có ẩn số là số phức.

• Tìm tập xác định và tập giá trị của hàm số có giá trị là số phức.

• Sử dụng số phức để mô tả các hình học trong không gian hai chiều, bao gồm điểm, đường thẳng, đường tròn và vectơ.

• Áp dụng số phức trong các bài toán cơ bản của điện xoay chiều và sóng điện từ.

Các dạng bài tập trên giúp củng cố kiến thức và kỹ năng tính toán về số phức, đồng thời giúp hiểu rõ hơn về tính chất và ứng dụng của số phức trong các lĩnh vực khác nhau của toán học và khoa học kỹ thuật.

Bài viết trên đây đã tổng hợp các kiến thức công thức số phức cho các bạn. Mong rằng với những gì chia sẻ sẽ giúp bạn đã nắm chắc và áp dụng tốt trong quá trình làm bài.