Cách tìm tập xác định của Hàm số mũ, Lũy thừa, Logarit đơn giản

Tìm hiểu kiến thức tìm tập xác định của Hàm số mũ, Lũy thừa, Logarit một cách dễ hiểu nhất và một số ví dụ vận dụng giúp nắm vững kiến thức toán lớp 12.

Hàm số mũ, hàm số Lũy thừa và hàm số Logarit là kiến thức quan trong của lớp 12. Nó chiếm một lượng lớn trong phần đại số. Ở đó tìm tập xác định của Hàm số mũ, Lũy thừa, Logarit là một mảng nhỏ nhưng có ý nghĩa rất quan trọng. Nó là nền tảng là cơ sở để người học có thể giải quyết những vấn đề phức tạp hơn. Hiểu được vấn đề đó thayphu.net sẽ giúp bạn đọc Nắm chắc kiến thức tìm tập xác định của Hàm số mũ, Lũy thừa, Logarit qua bài viết sau đây.

Tìm tập xác định của Hàm số mũ

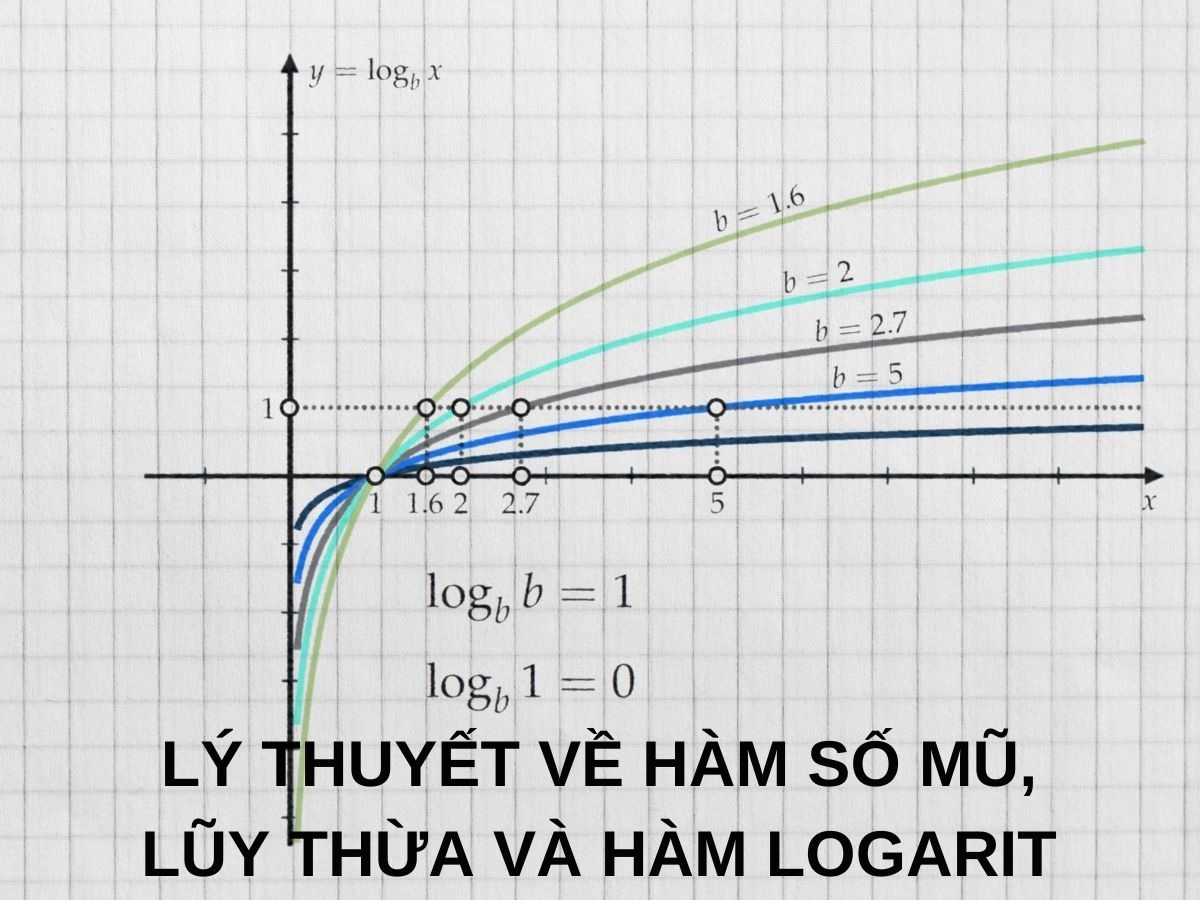
Tìm tập xác định của Hàm số mũ

Hàm số mũ có dạng: f(x) = a^x (a > 0; a ≠ 1)

Khi a > 1, a^x sẽ tăng vô hạn khi x tiến đến vô cùng và sẽ giảm xuống tới 0 khi x tiến đến âm vô cùng.

Khi 0 < a < 1, a^x sẽ giảm tới 0 khi x tiến đến vô cùng và tăng vô hạn khi x tiến đến âm vô cùng.

Đó là về mặt giá trị của hàm số f(x) = a^x. Còn Tập xác định của nó là R tức là không có điều kiện

Hàm số mũ có dạng y=a^f(x) (a > 0; a ≠ 1)

Tập xác định của hàm số dạng này ta cần tìm điều kiện để cho f(x) có nghĩa. Tùy vào từng trường hợp cụ thể mà người học áp dụng để tìm TXĐ.

Ví dụ 1: Tìm tập xác định của hàm số mũ y = 3^√(x +3)

Đáp án: Điều kiện x+3 ≥ 0 <=> x ≥ -3

Tập xác định là D = [-3; +∞)

Ví dụ 2: Tìm tập xác định của hàm số mũ y = 3^(4/(x2 – 4))

Đáp án: Điều kiện x2 – 4 ≠ 0 <=> x ≠ ±2

Tập xác định là D = R \ ±2

Ví dụ 3: Tìm tập xác định của hàm số mũ y = 10^(√x/(x2 – 9))

Đáp án: Điều kiện x2 – 9 ≠ 0 và x > 0 <=> x ≠ ±3 và x > 0.

Tập xác định là D = (0 ; +∞) \ 3

Tìm tập xác định của Hàm số lũy thừa

Khác với hàm số mũ Hàm số lũy thừa sẽ có dạng đảo lại. Đó là y = (f(x))a

Tập xác định của nó ngoài f(x) xác định còn phụ thuộc vào a. Ta sẽ có 3 trường hợp như sau:

• a nguyên dương: f(x) xác định
• a nguyên không dương: f(x) xác định và ≠ 0
• a không nguyên: f(x) xác định và f(x) > 0

Ví dụ 1. Tìm tập xác định của hàm số mũ y = (5/(x-3))2

Đáp án: Do 2 > 0 nên Điều kiện x – 3 ≠ 0 <=> x ≠ 3

Tập xác định là D = R \ 3

Ví dụ 2. Tìm tập xác định của hàm số mũ y = (x2 - 9)-2

Đáp án: Do -2 < 0 nên Điều kiện x2 – 9 ≠ 0 <=> x ≠ ±3

Tập xác định là D = R \ ±3

Ví dụ 3. Tìm tập xác định của hàm số mũ y = (x - 10)√5

Đáp án: Do √5 không nguyên nên Điều kiện x – 10 > 0 <=> x > 10.

Tập xác định là D = (10; +∞)

Tìm tập xác định của Hàm số Logarit

Tìm tập xác định của Hàm số Logarit

Hàm số Logarit có dạng f(x) = logaf(x), trong đó a > 0 và a ≠ 1

Tập xác định của hàm số này là f(x) xác định và f(x) > 0.

Bài tập kèm đáp án

Ví dụ 1. Tìm tập xác định Hàm số h(x) = log3(x - 2)

Đáp án: Hàm số có tập xác định D= (2, +∞), vì x - 2 >0 khi đó x > 2.

Ví dụ 2. Tìm tập xác định Hàm số f(x) = log4(x - 3) + log2(2x + 1)

Đáp án: Để log4(x - 3) xác định, ta cần đảm bảo x - 3 > 0, tức là x > 3. Do đó, tập xác định của log4(x - 3) là (3, +∞).

Để log2(2x + 1) xác định, ta cần đảm bảo 2x + 1 > 0, tức là x > -1/2. Do đó, tập xác định của log2(2x + 1) là (-1/2, +∞).

Tập xác định của hàm số f(x) được xác định bởi tập xác định chung của hai logarit, là tập giao của hai tập xác định trên: D(f) = (3, +∞) ∩ (-1/2, +∞) = (3, +∞).

Ví dụ 3: Tìm tập xác định

Hàm số f(x) = log3(x - 1) – log3(x + 2) + log3(x^2 - x - 6)

Đáp án:

Tập xác định của log3(x - 1) là (1, +∞).

Tập xác định của log3(x + 2) là (-2, +∞).

Tập xác định của log3(x^2 - x - 6) thì x^2 - x - 6 > 0, tức là (x - 3)(x + 2) > 0 <=> x < -2 hoặc x > 3.

Do đó, TXĐ của log3(x^2 - x - 6) là (-∞, -2) ∪ (3, +∞).

Tập xác định của hàm số f(x) được xác định bởi tập xác định chung của ba logarit, là tập giao của ba tập xác định trên:

D(f) = (1, +∞) ∩ (-2, +∞) ∩ (-∞, -2) ∪ (3, +∞) = (3, +∞).

Vậy, tập xác định của hàm số f(x) là (3, +∞).

Lời kết

Trên đây là những kiến thức cơ bản về tìm tập xác định của Hàm số mũ, hàm số Lũy thừa và hàm số Logarit. Thực tế nó không quá khó khăn. Có thể nói là khá đơn giản. Vì vậy bạn đọc hãy cố gắng nắm thật chắc nó và hãy ghé thăm web thayphu.net thường xuyên để cập nhật kiến thức về toán học nhé.