khối đa diện là gì? Nắm vững các loại khối đa diện trong 5 phút

Tìm hiểu chi tiết kiến thức về khối đa diện, giải thích định nghĩa, tính chất, công thức và các loại khối đa diện trong toán lớp 12.

Khối đa diện là kiến thức khá rộng và không dễ để chinh phục nó. Chương tình thuộc kiến thức hình học lớp 12 nên hay xuất hiện trong kỳ thi tốt nghiệp quốc gia. Do đó các sĩ tử phải nắm thật chắc kiến thức này để sẵn sàng cho kỳ thi. Hiểu được nhu cầu đó web thayphu.net sẽ đưa ra kiến thức về khối đa diện chi tiết nhất ở bài viết sau đây.

Khối đa diện là gì?

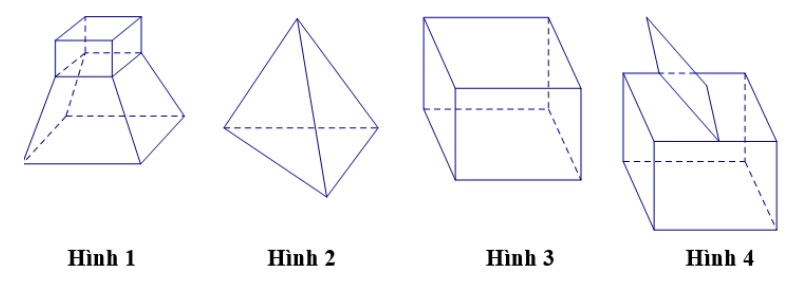
Phân biệt khối đa diện

Những hình chóp, hình lăng trụ, hình nón,.. đều là các khối đa diện. Cơ bản định nghĩa của nó là: Khối đa diện là một hình học không gian được tạo thành từ các mặt phẳng đa giác, được gọi là mặt đa diện, được nối với nhau theo các cạnh. Nó có thể được xác định bởi số lượng và hình dạng của các mặt phẳng, cạnh và đỉnh.

Từ khái niệm đó một khối đa diện phải thỏa mãn 2 điều kiện sau:

· Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.

· Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng 2 đa giác.

Ví dụ, một hình lập phương là một khối đa diện được tạo thành từ sáu mặt vuông, mỗi mặt có cạnh bằng nhau và cạnh giao nhau vuông góc. Một hình trụ là một khối đa diện được tạo thành từ một mặt tròn, được nối với một vòng tròn trên đỉnh và các cạnh thẳng giữa hai hình tròn đó.

Tính chất khối đa diện

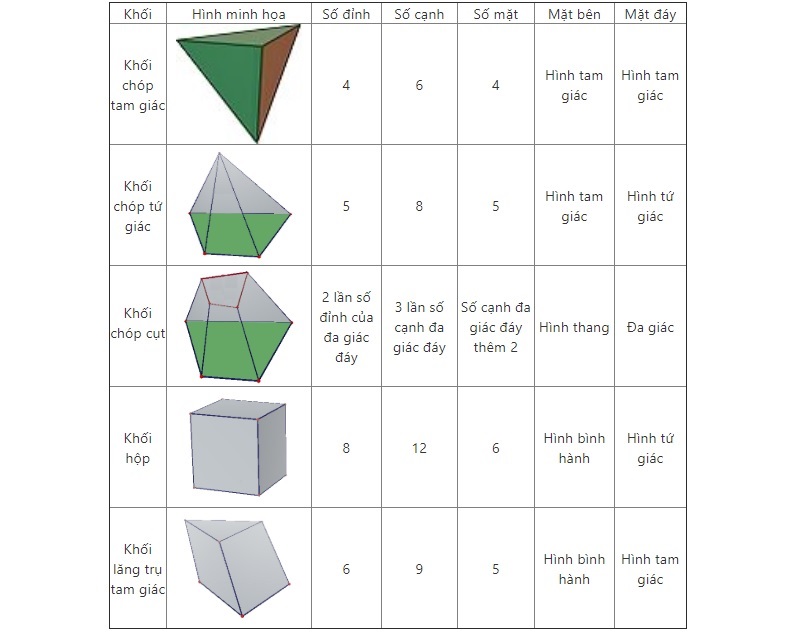
Tính chất khối đa diện

1. Diện tích bề mặt: là tổng diện tích của tất cả các mặt của khối đa diện.

2. Thể tích: là khối lượng của chất lưu trữ bên trong một khối đa diện.

3. Số đỉnh, cạnh và mặt: mỗi khối đa diện đều có một số đỉnh, cạnh và mặt cố định.

4. Góc của các mặt: góc của một mặt trong một khối đa diện là góc giữa hai đường thẳng chạm tại điểm giao giữa hai mặt đó.

5. Đường chéo: là đường thẳng nối hai đỉnh không liền kề trong một khối đa diện.

6. Đường trung trực: là đường thẳng cắt một mặt của khối đa diện sao cho tạo thành góc vuông với mặt đó và cắt đôi đoạn nối hai đỉnh không liền kề trên mặt đó.

7. Đường phân giác: là đường thẳng cắt đôi một góc hoặc đoạn thẳng trong một khối đa diện.

8. Đối xứng: một khối đa diện có thể có đối xứng tâm, đối xứng trục hoặc đối xứng mặt.

Đây là những tính chất cơ bản và quan trọng của khối đa diện. Dĩ nhiên phạm vi bài viết này không thể đi sâu phân tích mà chỉ có thể khái quát những nội dung cơ bản nhất cho bạn đọc.

Một số loại khối đa diện phổ biến

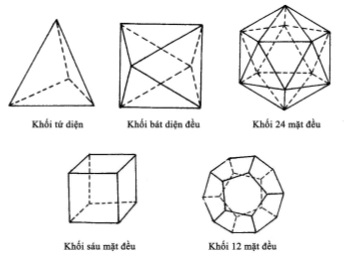
Các loại khối đa diện

· Khối đa diện đều: là một khối đa diện có tất cả các mặt phẳng đều là các hình đa giác đồng dạng, và tất cả các cạnh và góc của khối đều bằng nhau. Ví dụ: hình lập phương, hình chóp đều.

· Khối đa diện không đều: là một khối đa diện mà các mặt phẳng không phải đồng dạng và các cạnh có thể có độ dài khác nhau. Ví dụ: hình chóp không đều, hình hộp chữ nhật.

· Khối đa diện lồi: là một khối đa diện mà tất cả các điểm trên các cạnh nối giữa hai đỉnh của khối đều nằm bên trong khối đa diện. Ví dụ: hình lăng trụ, hình cầu.

· Khối đa diện lõm: là một khối đa diện mà tối thiểu một điểm trên các cạnh nối giữa hai đỉnh của khối nằm bên ngoài khối đa diện. Ví dụ: hình thập diện.

· Khối đa diện đặc biệt: là một loại khối đa diện có các đặc tính đặc biệt. Ví dụ: hình ngũ giác đều, hình bát giác.

Các công thức tính khối đa diện cơ bản

1. Khối lập phương (cube)

Diện tích mỗi mặt: S = a^2

Thể tích: V = a^3

Đường chéo: d = a√3

Trong đó a là đội dài của cạnh khối lập phương

2. Khối hình chóp tam giác (pyramid)

Diện tích đáy: S = 1/2 × b × h

Thể tích: V = 1/3 × S × H

Trong đó: b là độ dài của cạnh tam giác và h là chiều cao kẻ vuông góc kẻ với cạnh đó

H: Chiều cao của khối hình chóp

3. Khối hình trụ (cylinder)

Diện tích xung quanh: Sxq = 2πrh

Diện tích đáy: Sđ = πr^2

Thể tích: V = Sđ × h = πr^2h

Trong đó: r là bán kính hình tròn; h: chiều cao của khối hình trụ

4. Khối hình cầu (sphere)

Diện tích bề mặt: Sbm = 4πr^2

Thể tích: V = 4/3πr^3

Trong đó: r là bán kính hình cầu

5. Khối hình nón (cone)

Diện tích xung quanh: Sxq = πr√(r^2 + h^2)

Diện tích đáy: Sđ = πr^2

Thể tích: V = 1/3 × Sđ × H = 1/3πr^2h

Trong đó: r là bán kính; h: Chiều cao của khối hình nón

6. Khối tứ diện (tetrahedron)

Diện tích mỗi mặt: S = 1/2 × a × h

Thể tích: V = 1/3 × S × H

Trong đó: a là độ dài cạnh đáy; h: độ dài cạnh bên; H: chiều cao khối tứ diện.

Lời kết

Có thể thấy kiến thức về khối đa diện khá rộng và phức tạp. Đây là một nội dung quan trọng của chương trình hình học lớp 12. Do đó các sĩ tử hãy cố gắng chinh phục nó và hy vọng web thayphu.net đã cung cấp tới bạn đọc những thông tin hữu ích cho hành trình đó.