Bất đẳng thức Cauchy Toán lớp 10 và bài tập áp dụng

Bất đẳng thức Cauchy hay còn gọi là bất đẳng thức Cosi, là dạng kiến thức phổ biến và được áp dụng nhiều trong chương trình Toán lớp 10.

Khái niệm và các công thức chuẩn, công thức suy ra của bất đẳng thức Cauchy cùng với 3 cách chứng minh bất đẳng thức này rất dễ khiến các bạn nhầm lẫn khi giải bài tập. Chính vì thế, các bạn cố gắng nắm vững được nội dung bài học này, cùng với những lưu ý tránh nhầm lẫn khi học về bất đẳng thức này.

Cùng thayphu tìm hiểu bài học ngay sau đây, để áp dụng lý thuyết vào bài tập về chủ đề Toán học này một cách tốt hơn.

Khái niệm bất đẳng thức Cauchy

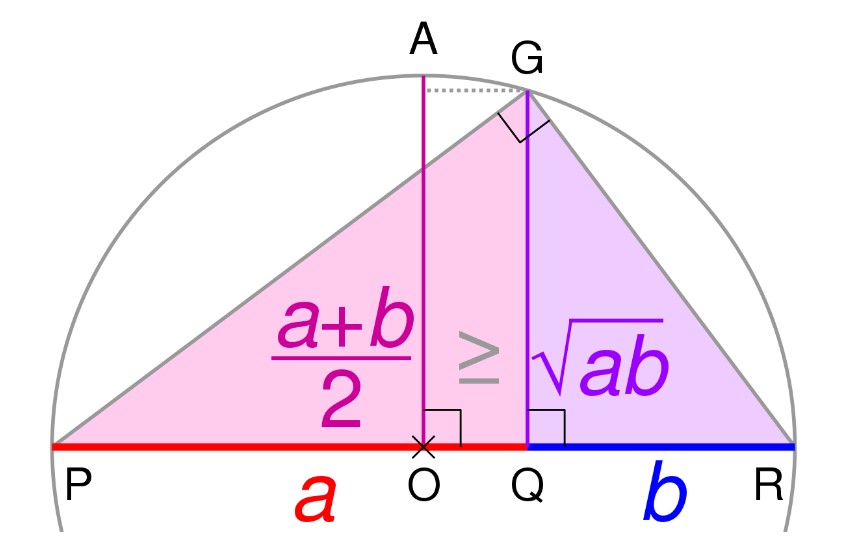
Khái niệm về bất đẳng thức Cauchy.

Khi đến với bộ môn Toán học thì cách gọi khác của bất đẳng thức Cauchy là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm. Trên thực tế thì tên gọi chính xác của bất đẳng thức phải là AM-GM vì cha đẻ của nó là nhà toán học Arithmetic mean và Arithmetic mean. Tuy nhiên về sau nhà toán học gốc Pháp Augustin – Louis Cauchy đã đưa ra một cách chứng minh đặc sắc và dễ hiểu nên nhiều người biết đến bất đẳng thức với cái tên Cauchy.

Bất đẳng thức Cauchy - Dạng tổng quát

Dạng tổng quát của bất đẳng thức Cauchy.

Các dạng tổng quát của bất đẳng thức được chia làm 2 dạng cho bất đẳng thức có 2 số và bất đẳng thức có n số.

Với bất đẳng thức có 2 số

Bất đẳng thức Cauchy được nêu đầy đủ như sau: Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, thêm nữa trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.

Biểu diễn: a+b2 ab , dấu = xảy ra khi và chỉ khi a=b

Với bất đẳng thức có n số

Với n số thực không âm x1, x2,…, xn thì bất đẳng thức Cauchy được biểu diễn dưới 3 dạng sau :

• Dạng 1 : x1 + x2 +… + xnn nx1. x2.… .xn
• Dạng 2 : x1+x2 + ... +xn n .nx1. x2.… .xn
• Dạng 3 : (x1 + x2 +… + xn n)n x1. x2.… .xn

Và trường hợp dấu = xảy ra khi và chỉ khi x1= x2 =… =xn

Với n số thực dương x1, x2,…, xn thì bất đẳng thức Cauchy được biểu diễn dưới 2 dạng :

• Dạng 1 : 1 x1+ 1x2+…+1xn n2 x1 + x2 +… + xn
• Dạng 2 : (x1+x2+...+xn).(1 x1+ 1x2+…+1xn ) n2

Và khi và chỉ khi x1= x2 =… =xn thì dấu = mới xảy ra.

Bất đẳng thức Cauchy - Dạng đặc biệt

Những dạng đặc biệt của bất đẳng thức cauchy.

Chứng minh bất đẳng thức Cauchy

Có 3 cách chứng minh bất đẳng thức Cauchy lần lượt là : Chứng minh bất đẳng thức với 2 số thực không âm, chứng minh bất đẳng thức với 3 số thực không âm, chứng minh bất đẳng thức với n số thực không âm. Cùng tìm hiểu kĩ hơn nhé !

Chứng minh bất đẳng thức với 2 số thực không âm

Có thể thấy với 2 số thực a,b không âm và đồng thời bằng 0 thì bất đẳng thức luôn đúng. Phần còn lại là chứng minh bất đẳng thức Cauchy với 2 số a, b dương là luôn đúng. Cách chứng minh như sau :

• a+b2 ab
• a+b2ab
• a-2ab +b0
• (a -b )2 0 (Luôn đúng

Suy ra, ta đã chứng minh được bất đẳng thức Cauchy luôn đúng với 2 số thực không âm.

Chứng minh bất đẳng thức với 3 số thực không âm

Với a, b, c đều bằng 0, bất đẳng thức Cauchy luôn đúng

Còn với 3 số a, b, c không âm ta chứng minh bất đẳng thức như sau:

• Đặt x=3a , y=3b , z=3c

⇒x,y,z≥0⇒x+y+z≥0

• Đến đây ta quay về chứng minh bất đẳng thức của 3 số thực x, y, z dương như sau: (x+y)3-3xy(x+y) + z3- 3 xyz 0
• Tiếp theo ta thực hiện triển khai hằng đẳng thức và nhân lần lượt các hệ số vào sao cho ra kết quả: (x+y+z).[(x-y)2+(y-z)2+(x-z)2]0

=> Khi đó dấu = xảy ra khi x=y=z hoặc a=b=c

Chứng minh bất đẳng thức Cauchy với n số thực không âm

Theo cách chứng minh bất đẳng thức Cauchy với 2 số dương đã trình bày ta được biểu thức luôn đúng. Tương tự với n = 2 thì bất đẳng thức luôn đúng.

Và để chứng minh bất đẳng thức luôn đúng với n số thì cần chứng minh nó cũng đúng với 2n số. Cách chứng minh như sau:

x1+x2 + ... +xn nnx1. x2.… .xn + nnxn+1 . xn+2... x2n 2n2nxn+1 . xn+2... x2n

Giả sử bất đẳng thức trên đúng với n số thì tương tự ta sẽ chứng minh nó đúng với n-1 số bằng cách sau :

x1+x2 + ... +xn nnx1. x2.… .xn

xn=Sn-1 với S=x1+x2+... +xn

S(n-1).n-1x1.x2... xn-1

Từ đây ta có thể kết luận bất đẳng thức Cauchy luôn đúng với n số thực không âm.

Ứng dụng của bất đẳng thức Cauchy

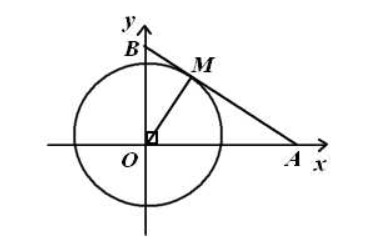
Ứng dụng của bất đẳng thức Cauchy được chia làm 3 mục chính bao gồm : Hệ quả, ý nghĩa đối với hình học, tính ứng dụng trong các lĩnh vực khác.

Hệ quả của bất đẳng thức Cauchy

Từ công thức tổng quát và các dạng đặc biệt của bất đẳng thức Cauchy ta có thể suy ra 3 hệ quả được áp dụng nhiều trong các dạng toán tìm số lớn nhất và số nhỏ nhất như sau :

• Giá trị tối thiểu đạt được của tổng của một số thực dương và nghịch đảo là 2.
• Tích 2 số thực dương đạt giá trị lớn nhất khi 2 số đó bằng nhau và điều kiện tiếp đến là tổng không đổi
• Tổng 2 số đó đạt giá trị nhỏ nhất khi 2 số đó bằng nhau và tích có giá trị không đổi.

Ý nghĩa hình học của các hệ quả được nêu

Ý nghĩa hình học của bất đẳng thức Cauchy

Rút ra từ 3 hệ quả trên, ta đúc kết được ý nghĩa hình học như sau :

• Hình vuông có diện tích lớn nhất trong các hình chữ nhật có cùng chu vi
• Hình vuông có chu vi nhỏ nhất trong các hình chữ nhật có cùng chu vi

Ứng dụng trong các lĩnh vực khác

Bất đẳng thức Cauchy không chỉ được vận dụng trong Toán học nói chung và các phương trình vô tỉ nói riêng. Mà nó còn xuất hiện trong bộ môn Vật Lý nhằm khảo sát công suất cực đại.

Một số đẳng thức suy ra từ bất đẳng thức Cauchy

Từ bất đẳng thức Cauchy, chúng ta cùng hiểu hơn về những dạng công thức được suy ra từ công thức chuẩn này nhé!

• x2+y22xy ; 2(x2+y2)(x+y)2 ; 2(x+y) x +y
• x2+y2- xy 3(x+y)24
• x2 +y2+z2xy+xz+yz
• 3(x2 +y2+z2)(x+y+z)23(xy+xz+yz)
• x2y2+ y2z2+z2x2xyz(x+y+z)

Các chú ý khi sử dụng bất đẳng thức Cauchy

Khi dùng bất đẳng thức Cauchy, các bạn có thể mắc một số lỗi như sau và lưu ý quan trọng cần nhớ, tránh nhầm lẫn.

• Khi áp dụng bất đẳng thức Cauchy thì phải là các số không âm
• Bất đẳng thức Cauchy thường được áp dụng trong các bất đẳng thức cần chứng minh có tổng và tích
• Điều kiện duy nhất để dấu = xảy ra là các số bằng nhau.

Bốn dạng bài tập liên quan đến bất đẳng thức Cauchy

Có 4 dạng bài tập vận dụng bất đẳng thức Cauchy:

• Vận dụng trực tiếp bất đẳng thức
• Kỹ thuật tách, thêm bớt, ghép cặp
• Kỹ thuật tham số hóa
• Kỹ thuật bất đẳng thức Cauchy ngược dấu

Bài viết trên đã tổng hợp các kiến thức liên quan đến bất đẳng thức Cauchy từ khái niệm đến các dạng biểu diễn tổng quát. Bất đẳng thức cauchy là một trong các nền tảng kiến thức Toán học quan trọng mà các bạn cần nắm vững. Hy vọng bài viết trên của thayphu.net đã giúp bạn làm được điều đó.