Tích vô hướng của hai vectơ lớp 10: lý thuyết và bài tập

Hoàn thành các bài tập tích vô hướng của hai vectơ lớp 10 các em hãy dành thời gian để ôn luyện các kiến thức cơ bản về định nghĩa, tính chất để có thể áp dụng hiệu quả.

Tích vô hướng của 2 vectơ là một nội dung mà các em học sinh sẽ được học trong chương trình lớp 10. Theo socolive tv (innocitysite.com), muốn chinh phục bất kỳ dạng bài nào chúng ta đều cần đọc hiểu phần lý thuyết. Bài viết sau đây của thayphu sẽ tổng hợp đầy đủ nội dung liên quan và bài tập tích vô hướng của hai vectơ lớp 10. Các em hãy cùng lướt chậm xem chi tiết để hiểu bài nhé!

Định nghĩa về vectơ

Tìm hiểu định nghĩa cùng các kiến thức cơ bản về tích vô hướng của hai vectơ

Cho đoạn thẳng AB có 2 điểm phân biệt là A và B. Trong toán học người ta sẽ dùng khái niệm vectơ để biểu diễn chiều đi từ A tới B hoặc từ B tới A. Chúng ta sẽ có vectơ AB trong trường hợp A là điểm đầu, B là điểm cuối. Hoặc ngược lại vectơ BA trong trường hợp B là điểm đầu và A là điểm cuối. Vì vậy để biểu diễn chiều đi của đoạn thẳng AB với 2 điểm phân biệt A và B, chúng ta sẽ sử dụng vectơ AB.

Định nghĩa: Vectơ hiểu đơn giản là một đoạn thẳng có hướng. Ký hiệu vectơ bằng cách dùng điểm đầu và điểm cuối để thể hiện bằng chữ in hoa hoặc cũng có thể là chữ thường.

Tích vô hướng của hai vectơ

Tích vô hướng là một phép toán lấy 2 chuỗi số có độ dài bằng nhau và cho kết quả là một số. Chúng ta cho 2 vectơ a và b đều khác vectơ 0. Tích vô hướng của hai vectơ a và b sẽ được xác định bởi công thức sau đây:

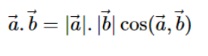
Trong trường hợp có ít nhất 1 trong 2 vectơ bằng vectơ 0 thì tích của hai vectơ cũng sẽ bằng 0.

Khi vectơ a và vectơ b đều khác vectơ 0 thì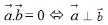

Khi hai vectơ a và b bằng nhau thì tích vô hướng sẽ là số bình phương vô hướng của vectơ a.

Các tính chất liên quan đến tích vô hướng của hai vectơ

Hiểu rõ phần lý thuyết sẽ giúp các em dễ dàng giải quyết bài tập tích vô hướng của hai vectơ lớp 10

Cho 3 vectơ a, b, c bất kỳ và mọi số thực k ta có các tích chất cơ bản như sau:

Từ tính chất về tích vô hướng của hai vectơ chúng ta có thể suy ra:

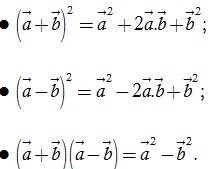
Biểu thức tọa độ của tích vô hướng

Trên mặt phẳng tọa độ Oij cho hai vectơ a=(a1, a2) và vectơ b=(b1,b2). Khi đó tích vô hướng của hai vectơ a và b sẽ bằng a1b1 + a2b2. Hai vectơ a và b đều khác vectơ 0 vuông góc với nhau khi và chỉ khi a1b1 + a2b2 = 0.

Đó là các kiến thức lý thuyết liên quan đến tích vô hướng, sau đây chúng ta sẽ cùng ứng dụng để thực hành giải bài tập.

Các dạng bài tập tích vô hướng của hai vectơ lớp 10

Cùng tham khảo các dạng bài tập liên quan đến tích vô hướng của hai vectơ

Các dạng bài tập tích vô hướng của hai vectơ lớp 10 khá đa dạng nhưng không quá khó. Các em chỉ cần nắm vững công thức và kỹ năng vận dụng thành thạo là được.

Bài tập dạng tính tích vô hướng

Cho hình vuông ABCD có tâm là O và cạnh bằng 1. Yêu cầu tính các tích các vectơ:

• Tích của vectơ OA và OB. Chúng ta có OA vuông góc với OB theo tính chất hình vuông 2 đường chéo vuông góc nên tích vectơ OA.OB sẽ bằng 0.
• Tích vectơ OA và OC. Đây là hai vectơ cùng phương, ngược chiều, có độ dài bằng nhau nên tích vectơ OA.OC sẽ bằng - OA bình phương và bằng -1/2 .

Bài tập tìm m để góc giữa 2 vectơ bằng 1 góc cho trước

Lúc này chúng ta thực hiện giải theo các bước:

• Đầu tiên là xác định vectơ nếu chưa có theo tham số m
• Tính độ dài của các vectơ theo tham số m
• Ứng dụng ngày công thức tính cos góc giữa hai vectơ đó là:

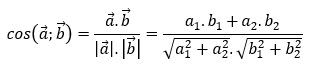
• Tiếp theo là đặt ra phương trình chứa ẩn m. Góc giữa hai vectơ bằng

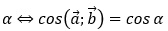
• Cuối cùng là giải phương trình và đưa ra giá trị của m.

Bài tập dạng công thức, cách tính độ dài đường trung tuyến

Đối với dạng bài tập này chúng ta áp dụng công thức tính độ dài đường trung tuyến. Cho tam giác ABC có các cạnh lần lượt là BC là a, CA là b, AB là c. Ta có ma, mb, mc là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và C của tam giác ABC. Khi đó ta sẽ có:

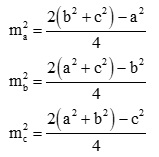
Ví dụ: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài các đường trung tuyến của tam giác ABC.

Chúng ta gọi độ dài trung tuyến từ các đỉnh A, B, C của tam giác ABC lần lượt là ma; mb; mc. Sau đó áp dụng các công thức trung tuyến ở trên. Vì độ dài các đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương.

Hy vọng qua các lý thuyết và dạng bài tập tích vô hướng của hai vectơ lớp 10 sẽ giúp ích cho các em. Chúc các em học tập tốt và có thể dễ dàng hoàn thành các đề bài, nâng cao điểm số môn Toán. Các em cũng đừng quên theo dõi kênh thường xuyên để cập nhật các kiến thức bổ ích khác nhé!