Tích có hướng của 2 vecto, tổng hợp kiến thức và bài tập áp dụng

Lý thuyết cơ bản, công thức và phương pháp giải tích có hướng của 2 vecto chi tiết nhất. Đi kèm các bài tập thực hành dễ hiểu nhất dành cho các em.

Tích có hướng của 2 vecto là một phần nội dung các em sẽ được làm quen trong chương trình Toán lớp 10. Bài viết sau đây của thayphu cung cấp lý thuyết cơ bản, công thức thức tính với phương pháp giải chi tiết. Từ đó các em dễ dàng vận dụng biết cách làm các bài tập liên quan đến tích có hướng của 2 vecto trong không gian.

Tìm hiểu kiến thức về tích có hướng 2 vecto

Định nghĩa tích có hướng

Tích có hướng là phép toán nhị nguyên trên các vecto trong không gian vecto ba chiều. Và cũng là trong 1 trong 2 phép nhân thường gặp giữa các vecto. Kết quả tích có hướng thu được là một giả vecto thay cho một vô hướng. Kết quả này sẽ vuông góc với mặt phẳng chứa 2 vecto đầu vào của phép tính.

Nếu n vuông góc với 2 vecto a, b thì suy ra -n cũng vậy. Việc chọn hướng của vecto n phụ thuộc vào hệ tọa độ theo quy tắc bàn tay trái và bàn tay phải. Để xác định các vecto a, b, a x b áp dụng cùng quy tắc với hệ tọa độ đang sử dụng.

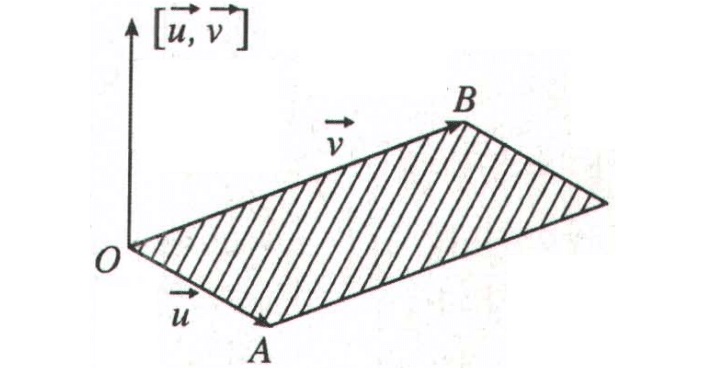
Cách xác định tích vecto trong không gian

Tính chất

• Phép tính này phản giao hoán: a x b = -b x a
• Nó phân phối được trên phép cộng vecto: a x (b + c) = a x b + a x c
• Kết hợp được với nhân vô hướng: (r.a) x b = a x (r.b) = r.(a x b)
• Phép tính không có tính kết hợp (a x b) x c khác a x (b x c)

Ví dụ: Khi a song song với b vế trái bằng 0 trong khi vế phải khác không.

• Phép tính thỏa mãn đẳng thức Jacobi: a x (b x c) + b x (c x a) + c x (a x b) = 0.

Nếu 2 vecto không cùng phương thì tích có hướng là vecto vuông góc với 2 vecto ban đầu.

Từ các tính chất trên, không gian vecto 3 chiều với phép nhân vecto tạo thành một đại số Lie.

Tích có hướng của 2 vecto

Tích có hướng của hai vecto u và vecto v trong không gian sẽ thỏa mãn 3 điều kiện:

• Vecto w có phương vuông góc với cả u và v
• |vecto w| = |vecto u|. |vecto v|. sin α, với α là góc hợp bởi vecto u và vecto v.
• Bộ 3 vecto (u, v, w) tạo thành một bộ ba thuận.

Tính chất vecto u || vecto v ⇔ [vecto u, vecto v] = vecto 0.

Công thức tọa độ tích có hướng của 2 vecto u = (u1; u2; u3) và vecto v = (v1; v2; v3) là

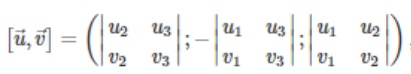
Trong đó định thức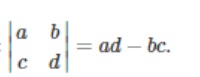

Ứng dụng của có tích có hướng của 2 vecto

• Diện tích tam giác: S(ABC) = ½ |[vecto AB, vecto AC]|
• Diện tích hình bình hành S(ABCD) = |[vecto AB, vecto AD]| = |[vecto AB, vecto AC]|
• Thể tích tứ diện: V(ABCD) = ⅙ |[vecto AB, vecto AC]. vecto AD|
• Thể tích khối hộp: V(ABCD.A’B’C’D’) = |[vecto AB, vecto AD]. vecto AA’|.

Lưu ý khi tiến hành giải bài các em có thể tính tích có hướng ở ngoài nháp theo các bước dễ hiểu như sau:

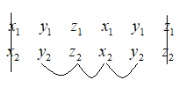
• Bước 1: Viết tọa độ mỗi vecto hai lần liền kề nhau, các tọa độ tương ứng của 2 vecto thẳng cột. Dạng bên dưới:

• Bước 2: Ta xóa đi 2 cột ngoài cùng

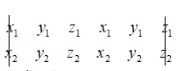
• Cuối cùng tính toán theo quy luật nhân chéo rồi trừ:

Các dạng bài tập áp dụng

Bài 1

Cho 2 vecto u = (1;5;3) và vecto v (2; -1;0) yêu cầu tính tích có hướng của 2 vecto trên.

Áp dụng phương pháp ở trên ta sẽ được

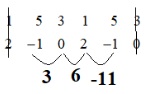
Kết luận [vecto u, vecto v] = (3;6;-11).

Bài 2

Trong hệ trục tọa độ Oxyz cho 4 điểm như sau: A (1;0; 1), B(-1;1;2), C(-1;1;0), D(2;-1;-2).

1. Hãy chứng minh rằng A, B, C, D là 4 đỉnh của một tứ diện
2. Hãy tính thể tích của tứ diện ABCD và độ dài đường cao đi qua đỉnh A.

Giải:

1. Theo đề bài cho ta có: vecto AB = (-2;1;1); vecto AC = (-2;1;-1); vecto AD = (1;-1;-3).

=> [vecto AB, vecto AC] = (-2;-4;0) => [vecto AB, vecto AC]. vecto AD = 2 khác 0.

=> vecto AB, vecto AC, vecto AD không đồng phẳng.

Vậy kết luận A, B, C, D là 4 đỉnh của một tứ diện.

2. Thể tích V của tứ diện ABCD = ⅙ |[vecto AB, vecto AC]. vecto AD| = 2/6 = ⅓.

Ta có vecto BC = (0;0;-2), vecto BD = (3;-2;-4).

=> [vecto BC, vecto BD] = (-4;-6;0) => S (BCD) = ½ |[vecto BC, vecto BD]| = căn 13.

Kết luận V(ABCD) = ⅓ d(A;(BCD)).S(BCD).

Bài 3

Trong không gian hệ trục tọa độ Oxyz cho 4 điểm A (-3;5;15), B(0;0;7), C(2;-1;4) và D(4;-3;0). Yêu cầu hãy chứng minh AB và CD cắt nhau.

Giải:

Theo đề bài ra ta có: vecto AB = (3;-5;-8); vecto AC = (5;-6;-11)

Vecto AD = (7;-8;-15), vecto CD = (2;-2;-4)

=> [vecto AB, vecto AC] = (7;-7;7) => [vecto AB, (AC)].(AD) = 0

=> vecto AB, vecto AC, vecto AD đồng phẳng

=> 4 điểm A, B, C, D cùng thuộc một mặt phẳng (1)

Bên cạnh đó [vecto AB, vecto CD] = (4;-4;4) khác vecto 0 ⇔ vecto AB, vecto CD không cùng phương (2).

Như vậy từ (1) và (2) ta kết luận AB và CD cắt nhau.

Vừa rồi là các lý thuyết và công thức liên quan đến tích có hướng của 2 vecto. Bên cạnh đó bài viết cũng đã đưa ra một số dạng bài tập thường gặp cho các em luyện tập, vận dụng. Chúc các em có những phút giây học tập bổ ích và đừng quên theo dõi kênh thường xuyên để cập nhật nhiều bài học mới nhé!