Tia phân giác là gì? Tổng hợp tính chất và bài tập vận dụng

Tia phân giác là gì? Tia phân giác của một góc chính là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

Lý thuyết về tia phân giác là gì? Các định lý về tính chất các điểm thuộc tia phân giác. Hãy cùng thayphu ôn tập lại các kiến thức trọng tâm và thực hành cùng các bài tập vận dụng có chọn lọc để hiểu bài tốt hơn nhé!

Định nghĩa tia phân giác là gì?

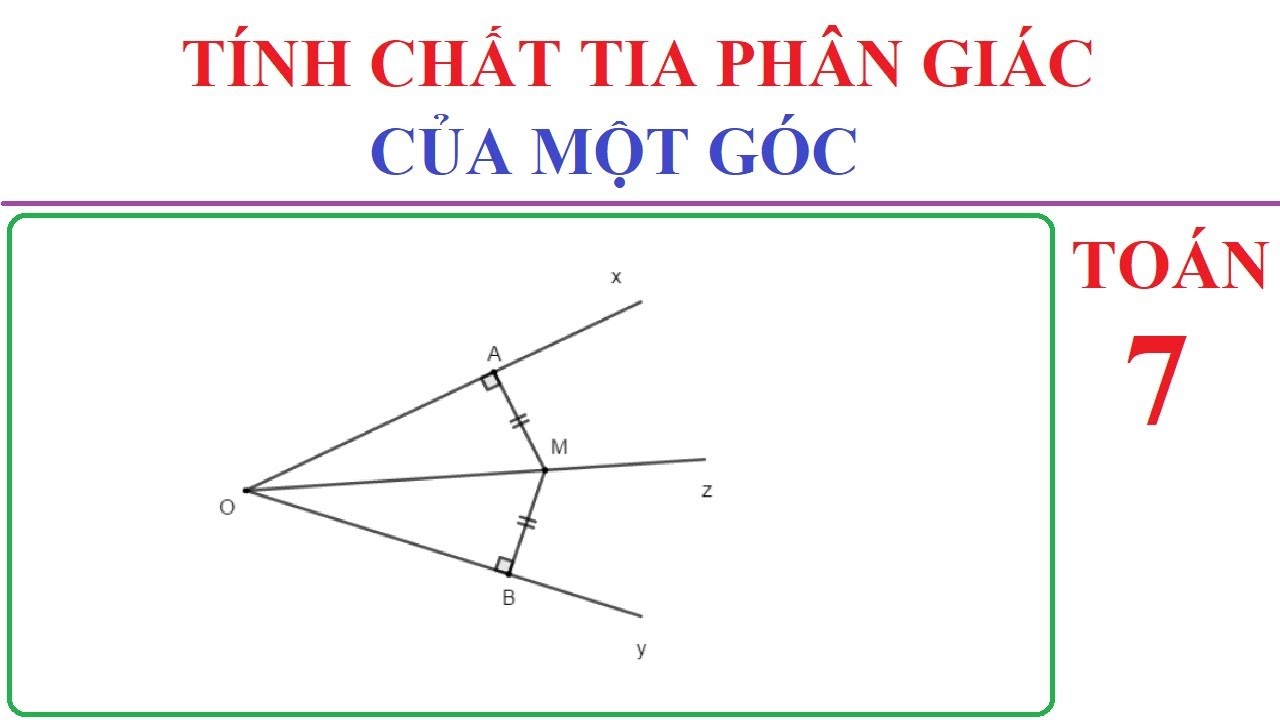
Tìm hiểu về tia phân giác là gì?

Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

Định lý về tính chất các điểm thuộc tia phân giác

Định lý thuận

Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.

Góc xOy với Oz là tia phân giác

M Oz

MA Ox; MB Oy

=> MA = MB

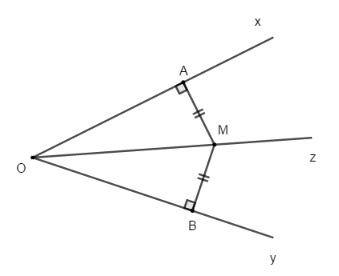
Định lý đảo

Điểm nằm bên trong một góc và cách đều hai cạnh của góc đó thì nằm trên tia phân giác của góc đó.

M xOy

MA Ox; MB Oy

MA = MB

=> M Oz

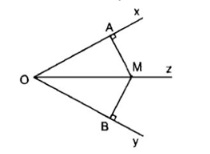
Nhận xét: Từ nội dung 2 định lý đảo và thuận trên ta có:

Tập hợp các điểm nằm bên trong một góc và cách đều 2 cạnh của góc là tia phân giác của góc đó.

Cách vẽ tia phân giác trong toán học

Cách 1: Dùng thước đo góc để vẽ tia phân giác của 1 góc.

Ví dụ: Vẽ tia phân giác của góc xOy = 60 độ

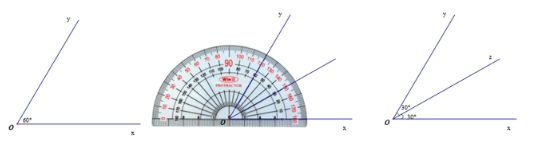
• Đầu tiên ta vẽ góc xOy = 60 độ
• Ta có: xOz = yOz và xOz + yOz = 60 độ nên suy ra xOz = 60 độ / 2 = 30 độ
• Sau đó dùng thước đo góc vẽ tia Oz đi qua 1 điểm trong của xOy sao cho xOz = 30 độ.
• Cuối cùng ta được tia Oz là tia phân giác của xOy

Lưu ý: Đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.

Ví dụ minh họa:

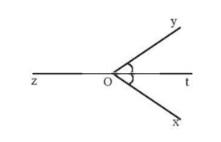
Trong hình tia Ot là tia phân giác của xOy

Lúc này đường thẳng zt gọi là đường phân giác của xOy.

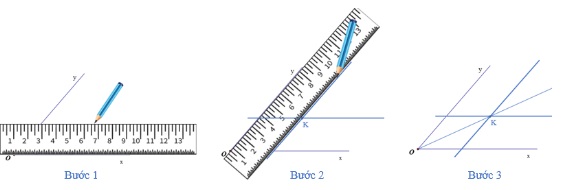
Cách 2: Dùng thước hai lề để vẽ tia phân giác

• Đặt thước sao cho 1 cạnh của thước trùng với 1 trong 2 cạnh của xOy. Dùng bút vạch 1 vạch thẳng theo cạnh kia của thước.
• Tiếp đó đặt thước sao cho 1 cạnh của thước trùng với cạnh còn lại của xOy. Rồi dùng bút vạch 1 đường thẳng theo cạnh kia của thước.
• Cuối cùng 2 nét vạch ở trên cắt nhau tại điểm K nằm trong xOy. Vẽ tia OK, tia này chính là tia phân giác của xOy.

Bài tập về tia phân giác là gì?

Bài tập 1

Chứng minh rằng trong 1 tam giác 3 phân giác của 2 góc ngoài và 1 góc trong không kề với chúng gặp nhau tại 1 điểm.

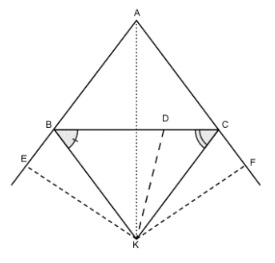
Cách giải:

Gọi K là giao điểm của 2 đường phân giác góc ngoài của góc B và góc C

Từ K hạ KD BC, KE AB, KF AC

Theo tính chất về đường phân giác ta có:

KD = KE

KD = KF

=> KE = KF

=> K nằm trên đường phân giác của góc BAC.

Vậy 2 phân giác góc ngoài của góc B, C và phân giác góc trong của góc A gặp nhau tại 1 điểm.

Bài tập 2

Cho tam giác ABC cân tại A, từ B kẻ đường BH vuông góc với AC tại H. Từ C kẻ đường CK vuông góc với AB tại K. Hai đường thẳng BH và CK cắt nhau tại I. Chứng minh AI là đường phân giác của tam giác ABC.

Cách giải:

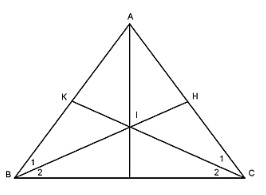
Xét tam giác ABH vuông tại H nên B1 + BAC = 90 độ

Tam giác ACK vuông tại K nên C1 + BAC = 90 độ

Do đó, B1 = C1 (cùng phụ BAC) (1)

Ta lại có: Tam giác ABC cân tại A nên ABC = ACB

Mà ABC = B1 + B2; ACB = C1 + C2

Nên B1 + B2 = C1 + C2 (2)

Từ (1) và (2) ta suy ra C2 = B2 (3)

Do vậy tam giác IBC cân tại I nên IB = IC (4)

Từ (3) và (4) ta có: Tam giác IHC = Tam giác IKB (cạnh huyền - góc nhọn) nên IH = IK

Kết luận AI là đường phân giác của góc BAC.

Bài tập 3

Cho tam giác ABC vuông tại B, dựng ở nửa mặt phẳng bờ BC, không chứa A, tam giác vuông CDB cân tại D. Chứng minh AD là tia phân giác của góc BAC.

Cách giải:

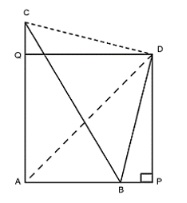
Ta hạ DP AB; DQ AC

Xét 2 tam giác DBP và DCQ có DPB = DQC = 90 độ

DB = DC (tam giác BDC vuông cân tại D) (1)

Ta có: DQ AC; AP AC

=> DQ // AP

Mà AP DP nên DQ DP => QDB + BDP = QDP = 90 độ

Lại có: QDB + QDC = BDC = 90 độ

(tam giác BDC vuông cân tại D)

Suy ra QDB + QDC = QDB + BDP

Do đó: BDP = QDC (cùng phụ với góc QDB) (2)

Từ (1) (2) => tam giác DBP = tam giác DCQ (cạnh huyền - góc nhọn)

Vậy nên DP = DQ

Điều đó chứng tỏ D nằm trên đường phân giác của góc BAC hay AD là đường phân giác của góc BAC.

Bài tập 4

Cho tam giác ABC, tia phân giác của góc C cắt AB tại điểm D. Trên tia đối của tia CA lấy điểm E sao cho CE = CB.

1. Chứng minh CD // EB
2. Tia phân giác của góc E cắt CD tại điểm F. Vẽ CK vuông góc EF tại K. Hãy chứng minh CK là tia phân giác của góc ECF.

Cách giải:

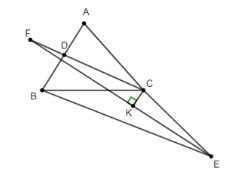
1. Tam giác CBE có CB = CE (giả thiết)

=> tam giác CBE cân tại C

Do đó CBE = CEB (tính chất tam giác cân)

Vì CD là tia phân giác của ACB (giả thiết)

Nên ACD = DCB = ACB / 2 hay ACB = 2ACD = 2DCB (1)

Ta lại có:

ACB = CBE + CBE = 2CBE (2)

Từ (1) và (2) => 2DCB = 2CBE hay DCB = CBE

Mà 2 góc này ở vị trí so le trong nên CD // EB

2. Vì CD // EB (chứng minh trên) nên CFE = FEB (vị trí so le trong)

Bên cạnh đó: CEF = FEB (vì EF là tia phân giác)

=> CFE = CEF (= FEB)

Suy ra tam giác CFE cân tại C.

Mặt khác: CK FE tại K => CK là đường cao

Vậy nên CK đồng thời là đường phân giác của góc ECF (tính chất tam giác cân)

Bài tập 5

Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường thẳng vuông góc với BC tại trung điểm của BC ở điểm D. Gọi H và K là chân các đường vuông góc kẻ từ D đến các đường thẳng AB, AC. Hãy chứng minh rằng BH = CK.

Cách giải:

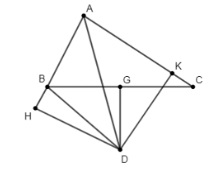
Ta có điểm D thuộc phân giác của góc A

DH vuông góc với AB, DK vuông góc với AC

Suy ra DH = DK (tính chất tia phân giác của 1 góc)

Gọi G là trung điểm của BC

Xét 2 tam giác BGD và CGD ta có:

BGD = CGD = 90 độ (DG là đường trung trực của BC)

BG = CG (giả thiết)
DG là cạnh chung

Vậy nên tam giác BGD = tam giác CGD (2 cạnh góc vuông)

=> BD = CD (2 cạnh tương ứng)

Xét 2 tam giác BHD và CKD ta có:

BHD = CKD = 90 độ

DH = DK (chứng minh trên)

BD = CD (chứng minh trên)

Vậy nên tam giác BHD = tam giác CKD (cạnh huyền - cạnh góc vuông)

Kết luận BH = CK (2 cạnh tương ứng)

Bài viết đã giúp các em ôn tập lại kiến thức tia phân giác là gì, các định lý và tính chất liên quan. Hãy cùng tham khảo ngay các bài tập cụ thể có kèm lời giải để hiểu bài hơn nhé!