Tam giác bằng nhau, các trường hợp cụ thể và bài tập

Hai tam giác bằng nhau khi có các cạnh và các góc tương ứng bằng nhau. Các trường hợp cụ thể là cạnh - cạnh - cạnh, cạnh - góc - cạnh và góc - cạnh - góc.

Kiến thức về hai tam giác bằng nhau là một nội dung quan trong chương trình Toán lớp 7. Dưới đây thayphu sẽ hệ thống lại các trường hợp của 2 tam giác giác bằng nhau, hệ quả và các dạng bài tập liên quan kèm ví dụ minh họa giúp các em dễ hiểu. Hãy cùng đón xem ngay!

Lý thuyết hai tam giác bằng nhau

Tìm hiểu về hai tam giác bằng nhau

Khái niệm

Hai tam giác bằng nhau là 2 tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

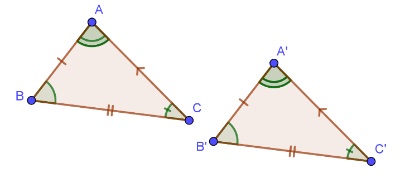
Hai tam giác ABC và A’B’C’ bằng được viết dưới dạng: ABC = A’B’C’

ABC = A’B’C’ nếu AB = A’B’, BC = B’C’, CA = C’A’

A = A', B = B', C = C'

Các trường hợp bằng nhau của 2 tam giác thường

Trường hợp 1: Cạnh - cạnh - cạnh (c.c.c)

Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì 2 tam giác đó bằng nhau.

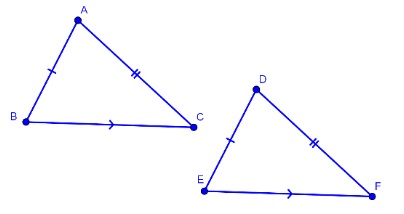
Xét 2 tam giác ABC và DEF ta có: AB = DE, BC = EF, CA = FD

=> ABC = DEF (c.c.c)

Trường hợp 2: Cạnh - góc - cạnh (c.g.c)

Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa của tam giác kia thì 2 tam giác đó bằng nhau.

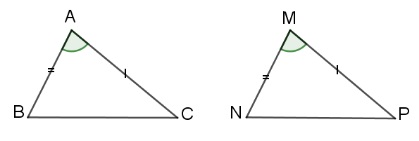
Xét 2 tam giác ABC và MNP có: AB = MN, A = M, AC = MP

=> ABC = MNP (c.g.c)

Hệ quả: Nếu 2 cạnh góc vuông của 2 tam giác vuông này lần lượt bằng 2 cạnh góc vuông của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.

Trường hợp 3: Góc - cạnh - góc (g.c.g)

Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 góc và 2 góc kề của tam giác kia thì 2 tam giác đó bằng nhau.

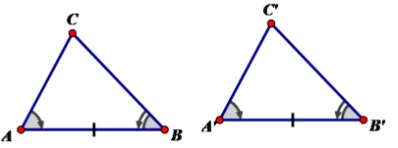
Xét 2 tam giác ABC và A’B’C’ có: A = A’, AB = A’B’ và B = B’

=> ABC = A’B’C’ (g.c.g)

Hệ quả:

• Nếu 1 cạnh góc vuông và góc nhọn kề với cạnh ấy của tam giác vuông này bằng cạnh góc vuông và góc nhọn kề với cạnh ấy của tam giác vuông kia thì 2 tam giác đó bằng nhau.
• Nếu cạnh huyền và 1 góc nhọn của tam giác vuông này bằng cạnh huyền và 1 góc nhọn của tam giác vuông kia thì 2 tam giác vuông đó bằng nhau.

Các dạng bài tập về hai tam giác bằng nhau

Dạng 1 - Tính độ dài đoạn thẳng, tính số đo góc, chứng minh 2 cạnh, 2 góc bằng nhau

Phương pháp giải: Từ 2 tam giác bằng nhau ta suy ra các cạnh, các góc tương ứng bằng nhau.

Lưu ý: Căn cứ vào quy ước viết các đỉnh tương ứng của 2 tam giác bằng nhau theo đúng thứ tự. Từ đó ta viết được các góc bằng nhau, các đoạn thẳng bằng nhau.

Bài tập minh họa:

Cho tam giác ABC = tam giác MNP, biết góc A = 80 độ, góc P = 40 độ, BC = 5cm. Tính số đo các góc còn lại của tam giác MNP và độ dài của cạnh NP.

Cách giải:

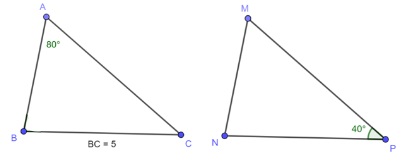
Ta có: ABC = MNP (theo đề cho)

Theo định nghĩa của 2 tam giác bằng nhau:

BC = NP = 5cm

A = M = 80 độ

C = P = 40 độ

Sử dụng định lý về tổng 3 góc trong tam giác MNP ta có:

M + N + P = 180 độ

=> N = 180 độ - M - P = 180 độ - 80 độ - 40 độ = 60 độ

Vậy M = 80 độ, N = 60 độ và NP = 5cm.

Dạng 2: Vẽ tam giác khi biết độ dài 3 cạnh, biết 2 cạnh và 1 góc xen giữa hoặc 1 cạnh và 2 góc kề

Phương pháp giải:

1. Vẽ tam giác ABC khi biết độ dài của 3 cạnh

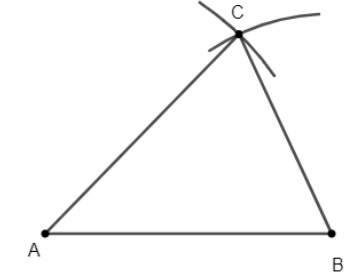
• B1: Vẽ 1 trong 3 đoạn thẳng cho trước, chọn đoạn AB
• B2: Vẽ cung tròn tâm A bán kính AC
• B3: Vẽ cung tròn tâm B bán kính BC, 2 cung tròn này cắt nhau tại C
• B4: Ta nối CA, CB ta sẽ được tam giác ABC cần vẽ.

2. Vẽ tam giác ABC biết độ dài 2 cạnh AB, AC và góc BAC xen giữa:

• B1: Vẽ xAy = BAC
• B2: Xác định điểm C thuộc tia Ax có độ dài AB cho trước
• B3: Xác định điểm C thuộc tia Ay có độ dài AC cho trước
• B4: Vẽ đoạn thẳng BC chúng ta được tam giác ABC cần vẽ

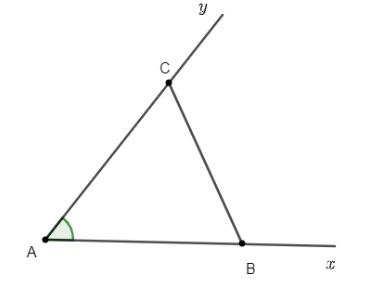
3. Vẽ tam giác ABC biết độ dài cạnh AB và 2 góc kề là góc BAC và ABC:

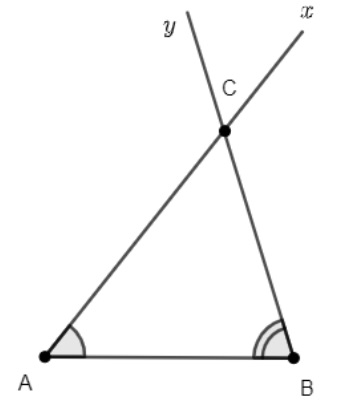
• B1: Vẽ đoạn AB
• B2: Trên cùng 1 nửa mặt phẳng bờ AB, vẽ các tia Ax và By sao cho BAx = BAC , ABy = ABC
• B3: Cho 2 tia Ax và By cắt nhau tại điểm C, ta được tam giác ABC cần vẽ.

Bài tập minh họa:

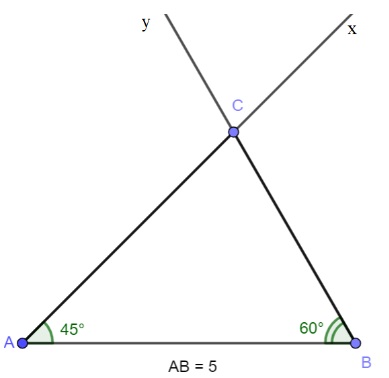
Hãy vẽ tam giác ABC biết AB = 5cm, BAC = 45 độ, ABC = 60 độ

Cách giải:

Đầu tiên là vẽ đoạn thẳng AB = 5cm

Trên cùng 1 nửa mặt phẳng bờ AB, ta vẽ các tia Ax và By sao cho BAx = 45 độ, ABy = 60 độ. 2 tia Ax và By cắt nhau tại điểm C. Như vậy ta được tam giác ABC cần vẽ.

Dạng 3: Chứng minh 2 tam giác bằng nhau theo c.c.c, c.g.c, g.c.g

Phương pháp giải:

• Đầu tiên ta xét 2 tam giác
• Sau đó kiểm tra 3 điều kiện bằng nhau: cạnh - cạnh - cạnh, cạnh - góc - cạnh và góc - cạnh - góc
• Cuối cùng kết luận 2 tam giác bằng nhau.

Bài tập minh họa:

Cho tam giác MNP có PM = PN, hãy chứng minh PMN = PNM bằng 2 cách.

Cách giải:

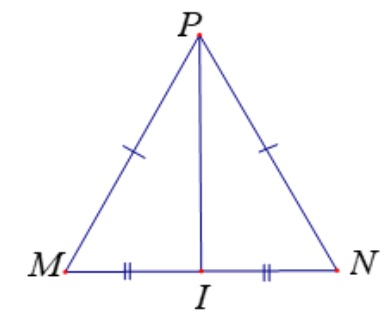
Ta lấy điểm I là trung điểm của MN rồi I với P.

Xét 2 tam giác MIP và NIP có:

MI = NI (I là trung điểm của MN)

Cạnh chung là IP

PM = PN (giả thiết)

Vì vậy MIP = NIP (c.c.c)

=> PMI = PNI (2 góc tương ứng bằng nhau) hay PMN = PNM (đpcm)

Cách 2:

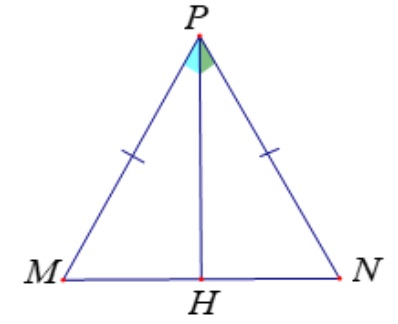
Ta kẻ tia phân giác PH của góc MPN cắt MN tại điểm H.

Xét 2 tam giác MPH và NPH có:

PM = PN (theo giả thiết)

MPH = HPN (PH là tia phân phân giác của góc MPN

Cạnh chung là PH

=> MPH = NPH (c.g.c)

Vì vậy PMH = PNH (2 góc tương ứng bằng nhau) hay PMN = PNM (đpcm)

Bài viết vừa trình bày đầy đủ về khái niệm, các trường hợp bằng nhau của 2 tam giác thường, hệ quả và các dạng bài tập liên quan. Các em hãy cùng ôn tập lại để nắm vững kiến thức và làm tốt các đề thi sắp tới nhé!