Phương trình và bất phương trình chứa trị tuyệt đối

Để giải phương trình và bất phương trình chứa trị tuyệt đối lớp 10 chúng ta thường sử dụng định nghĩa hoặc tính chất của giá trị tuyệt đối để khử dấu.

Cách giải phương trình và bất phương trình chứa trị tuyệt đối lớp 10 sẽ được xoilac tv (congdonggioi.com) tổng hợp chi tiết, đây là một phần quan trọng trong bộ môn Toán. Vậy khi gặp dạng bài này các em cần biết cách giải, trước hết cũng cần phải nắm vững các lý thuyết, tính chất cũng như cách giải bất phương trình chứa trị tuyệt đối.

Tìm hiểu về giá trị tuyệt đối

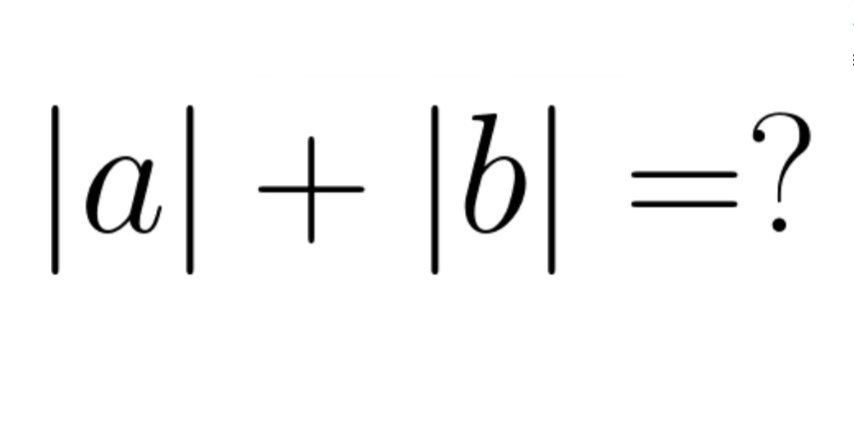
Cùng tìm hiểu lý thuyết về trị tuyệt đối để hiểu rõ rồi thực hiện bài tập hiệu quả hơn

Giá trị tuyệt đối hay còn được gọi là mô đun của số thực a, ký hiệu là |a|. Khi a > hoặc = 0 thì |a| = a, khi a < 0 thì |a| = -a.

Như vậy giá trị tuyệt đối của một số bất kỳ chính là khoảng cách từ số đó cho đến 0. Giá trị tuyệt đối của một số dương là chính số đó, còn trị tuyệt đối của số âm là số đối của nó.

Lưu ý các tính chất của giá trị tuyệt đối như sau:

• Giá trị tuyệt đối của mọi số, kể cả âm hay dương đều sẽ không âm.
• Giá trị tuyệt đối của hai số đối nhau hay có giá trị bằng nhau trên cùng trục số thì sẽ bằng nhau và ngược lại.
• Trong 2 số âm, số có trị tuyệt đối nhỏ hơn thì số đó lớn hơn. Ngược lại trong 2 số dương, số có trị tuyệt đối nhỏ hơn thì vẫn nhỏ hơn.
• Bình phương giá trị tuyệt đối của 1 số cũng bằng bình phương của chính nó.
• Mọi số đều có giá trị bằng hoặc lớn hơn số đối của trị tuyệt đối của chính nó và bằng hoặc nhỏ hơn trị tuyệt đối của số đó.
• Trị tuyệt đối của một tích bằng tích của hai trị tuyệt đối và trị tuyệt đối của thương bằng thương của hai trị tuyệt đối.
• Tổng của 2 trị tuyệt đối luôn bằng hoặc lớn hơn trị tuyệt đối của tổng 2 số đó.

Phương trình và bất phương trình chứa trị tuyệt đối lớp 10

Phương trình và bất phương trình chứa trị tuyệt đối lớp 10 là một nội dung quan trọng các em cần nắm vững

Bất phương trình chứa trị tuyệt đối là bất phương trình có chứa ẩn trong dấu giá trị tuyệt đối với 2 dạng cơ bản là: |f(x)| > |g(x)| hoặc |f(x)| < |g(x)|.

Chúng ta cần giải bất phương trình chứa trị tuyệt đối theo các bước như sau:

• Thứ nhất: Sau khi đọc kỹ đề bài, phải áp dụng những định nghĩa về dấu giá trị tuyệt đối để bỏ đi dấu trị tuyệt đối trong bài.
• Thứ 2: Tiến hành giải bất phương trình như bình thường.
• Thứ 3: Sau khi giải ra nhiều trường hợp, chúng ta cần kết hợp với điều kiện để chọn đúng nghiệm thích hợp nhất.
• Thứ 4: đưa ra kết luận cuối cùng.

Cách giải phương trình và bất phương trình chứa trị tuyệt đối lớp 10

Cùng tham khảo các dạng bài tập và cách giải để luyện tập thành thạo nội dung này

Khi gặp các bài tập liên quan đến phương trình hay bất phương trình chứa trị tuyệt đối các em cần ghi nhớ lý thuyết cơ bản. Sau đó xác định chúng có nằm trong những cơ bản này: |f(x)| > |g(x)| hay |f(x)| > g(x) hay |f(x)| < g(x). Nếu là 1 trong 3 dạng này các em có thể áp dụng các phương pháp như sau:

Thứ nhất: Dùng định nghĩa để khử trị tuyệt đối

Dựa vào định nghĩa |f(x)| = f(x) khi f(x) > 0 hay |f(x)| = -f(x) khi f(x) < 0 để khử trị tuyệt đối của bất phương trình.

• Ví dụ 1 :đề bài yêu cầu giải bất phương trình |3 - 2x| < x + 1

Như vậy khi kết hợp cả hai trường hợp ta sẽ có ⅔ < x < 4.

Kết luận tập nghiệm của bất phương trình là S = (⅔; 4).

• Ví dụ 2: Giải bất phương trình chứa trị tuyệt đối như sau: |5x - 4) >= 6

Giải: |5x - 4) >= 6

Thứ hai: Bình phương 2 vế

Chúng ta có 1 số cách bình phương 2 vế như:

• |f(x)| > |g(x)| tương đương (f(x)) ^2 > (g(x))^2
• |f(x)| > |g(x)| tương đương g(x) < 0 hoặc [g(x) 0 và f^2(x) > g^2(x)]
• |f(x)| > |g(x)| tương đương g(x) > 0 và f(x)^2 < [g(x)]^2

Ví dụ 1: Giải bất phương trình

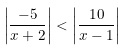
Điều kiện xác định là x khác 1 và x khác -2.

Tiến hành bình phương 2 vế ta sẽ có:

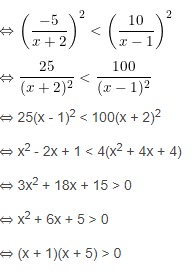
Ta thấy (x + 1) (x + 5) > 0 khi x < -5 hoặc x > -1. Kết hợp với điều kiện ở trên và đi đến kết luận tập nghiệm của bất phương trình.

Ví dụ 2: Giải các bất phương trình có trị tuyệt đối như sau:

1. |2x - 9) <= x + 2
2. |2x - 3| >= x + 2

Giải:

Thứ 3: Lập bảng xét dấu để khử trị tuyệt đối

Một trong những cách giải phương trình và bất phương trình chứa trị tuyệt đối lớp 10 thường dùng là lập bảng xét dấu. Do đó chúng ta cần kết hợp bảng xét dấu nhị thức bậc nhất với tam thức bậc hai.

Ví dụ 1: Giải bất phương trình: |2x - 2| + |3 - x| > 3

Tiến hành bỏ dấu giá trị tuyệt đối ở vế trái và lập bảng ta có:

Ví dụ 2: Giải phương trình |x^2 - x| + |2x - 1| = 1

Chúng ta sẽ lập bảng xét dấu và giải theo các bước sau:

Thông qua các nội dung về lý thuyết cùng bài tập về phương trình và bất phương trình chứa trị tuyệt đối lớp 10 trên đây hy vọng giúp các em bổ sung nhiều kiến thức. Chúc các em học tốt và gia tăng điểm số môn Toán như ý. Các bạn đừng quên ghé thăm trang web của thayphu.net để cập nhật các bài viết mới của kênh để xem thêm nhiều nội dung hữu ích nhé!