Phương pháp giải phương trình và bất phương trình chứa căn

Cách giải các phương trình và bất phương trình chứa căn. Đi kèm các nguyên tắc quan trọng và ví dụ minh họa dễ hiểu.

Phương trình và bất phương trình chứa căn là dạng toán thường hay gặp trong chương trình Toán THPT. Bởi vậy các em cần hiểu và ghi nhớ công thức để hoàn thành tốt các bài tập. Đặc biệt quá trình giải toán cũng bắt buộc phải có sự đánh giá cẩn thận.

Bài viết sau đây của thayphu sẽ giới thiệu cho các em nguyên tắc quan trọng, phương pháp giải và ví dụ minh họa dễ hiểu nhất.

Định nghĩa về phương trình và bất phương trình chứa căn

Nắm lòng các kiến thức sẽ giúp các em hoàn thành tốt mọi dạng bài tập

Phương trình chứa căn và bất phương trình là những nội dung khó và phức tạp. Ta sẽ có các công thức cơ bản như sau:

• Công thức 1 có dạng:

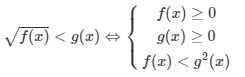
Nếu như có thêm dấu = thì ta có:

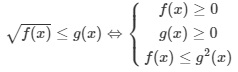
Để bất phương trình xác định chúng ta cần điều kiện là f(x) không âm. Để 2 vế không âm thì g(x) không âm. Như vậy mới có thể tiến hành bình phương cả 2 vế.

• Công thức 2 có dạng:

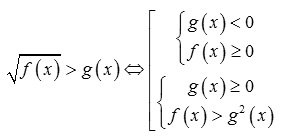
Trong trường hợp có thêm dấu = thì ta có:

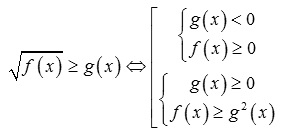
Khi g(x) âm thì chỉ cần bất phương trình xác định vì căn bậc hai không bao giờ âm. Nếu g(x) không âm thì bình phương 2 vế ta có f(x) lớn hơn hoặc = g^2(x). Bởi vậy không cần có điều kiện f(x) không âm nữa.

Các phương pháp giải phương trình và bất phương trình chứa căn

Các phương pháp giải bất phương trình chứa căn

Khi gặp các bài toán về bất phương trình chứa căn, nhiều em rơi vào lúng túng chưa biết dùng cách nào. Chỉ cần ghi nhớ các phương pháp cơ bản sau thì các em sẽ dễ dàng chinh phục đề bài thôi.

Phương pháp 1 - Sử dụng định nghĩa để bỏ căn

Đây là phương pháp được sử dụng phổ biến nhất để giải bất phương trình căn thức. Các em có thể dùng nó để giải các dạng bất phương trình đã kể trên.

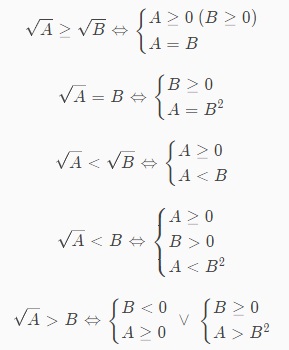
Để bất phương trình xác định cần có điều kiện A và B không âm, sau đó thực hiện bình phương 2 vế.

Bài tập áp dụng

Giải bất phương trình:

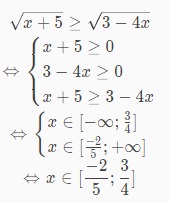
Phương pháp 2 - Biến đổi tương đương

Các em học sinh sử dụng phép biến đổi tương đương bằng cách bình phương 2 vế của bất phương trình. Ta sẽ có dạng 1 như sau:

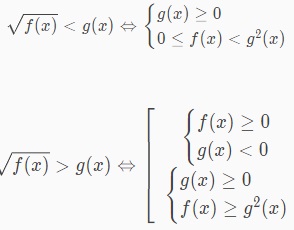
Khi gặp các dạng bài này các em lưu ý thực hiện theo các bước như sau:

• Đầu tiên là tìm điều kiện xác định
• Tiếp đó sử dụng phép biến đổi tương đương để đưa bất phương trình chứa căn về hệ bất phương trình đại số.
• Cuối cùng là xác định nghiệm x và so sánh với các điều kiện để đi đến kết luận.

Bài tập ứng dụng

Yêu cầu giải bất phương trình:

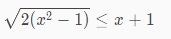
Ta có điều kiện xác định là x^2 - 1 >= 0 ⇔ x thuộc R \ (-1;1)

Vận dụng phương pháp biến đổi tương đương, bất phương trình trên sẽ tương đương với:

x+1 >= 0 ⇔ x >= -1

2(x^2 - 1) < (x + 1)^2 ⇔ x thuộc (-1;3)

Như vậy khi đối chiếu với điều kiện thì chúng ta kết luận tập nghiệm là x thuộc (-1;3).

Phương pháp 3 - Tiến hành đặt ẩn phụ

Đặt ẩn phụ cũng là một cách giúp đơn giản hóa phương trình và bất phương trình chứa căn. Chúng ta sẽ đặt ẩn phụ để chuyển bất phương trình căn thức về bất phương trình đại số không chứa căn. Và ẩn phụ được đặt cho chính biểu thức chứa căn.

Bài tập ứng dụng

Yêu cầu giải bất phương trình như sau:

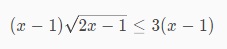
Ta có điều kiện xác định là 2x - 1 >= 0 ⇔ x >= ½

Chúng ta tiến hành đặt:

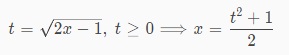
Như vậy bất phương trình đã cho sẽ trở thành:

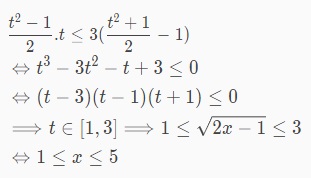
Kết luận phương trình có nghiệm là 1 <= x <= 5.

Nguyên tắc khi giải bất phương trình chứa căn

Lưu ngay nguyên tắc khi giải bất phương trình chứa căn

Các dạng bất phương trình chứa căn thường gặp sẽ bao gồm:

• Bất phương trình chứa căn cơ bản
• Quy bất phương trình chứa căn về hệ bất phương trình không chứa căn
• Sử dụng bất phương trình tương đương hoặc hệ quả khi giải bất phương trình có ẩn trong dấu căn
• Hệ bất phương trình có chứa căn thức
• Vận dụng phương pháp chiều biến thiên của hàm số khi giải bất phương trình chứa căn
• Vận dụng phương pháp đánh giá 2 vế khi giải phương trình và bất phương trình chứa căn.

Những dạng này cũng sẽ được áp dụng trong các bài toán bất phương trình khác. Song nếu như sử dụng phương pháp biến đổi tương đương với các bất phương trình có chứa căn thì bậc của các biến sẽ rất lớn.

Để khử dấu căn của phương trình, bất phương trình thì ta tiến hành bình phương 2 vế. Với điều kiện là cả 2 vế phương trình, bất phương trình đều không âm. Như vậy mới có thể đảm bảo có một phương trình, bất phương trình mới tương đương.

Tổng kết

Qua bài viết này chắc hẳn các em học sinh đã có thể ghi nhớ những kiến thức quan trọng và bỏ túi cho mình các phương pháp giải phương trình và bất phương trình trình chứa căn hữu hiệu nhất. Hãy cùng thực hành thêm các bài tập để thành thạo và nâng cao kỹ năng giải toán. Chúc các em sẽ luôn giành được thật nhiều điểm tốt trong các bài kiểm tra cũng như kỳ thi sắp tới. Đừng quên theo dõi kênh để xem thêm nhiều bài học hay, dễ hiểu nhất nhé!