Phương trình đường phân giác của góc tạo bởi 2 đường thẳng cho trước

Phương trình đường phân giác của góc tạo bởi 2 đường thẳng chi tiết dễ ghi nhớ. Học sinh có thể tham khảo và ghi và giấy để phục vụ cho học tập sau này.

Phương trình đường phân giác của góc tạo bởi 2 đường thẳng được dùng trong toán học hình học rất phổ biến. Nó được áp dụng ở tất cả các bài học và đặc biệt ở các kỳ thi học kỳ và THPT. Hãy cùng thayphu tìm hiểu về những công thức toán hình học để có thể học giỏi hơn mỗi ngày nhé!

Lý thuyết phương trình đường phân giác của góc tạo bởi 2 đường thẳng

Phương trình đơn giản và dễ nhớ

Phương trình đường phân giác của góc tạo bởi 2 mặt phẳng sẽ có những khái niệm sau:

• Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo ra hai góc bằng nhau với hai cạnh đó.
• Đường phân giác của một góc là đường thẳng chứa tia phân giác của góc đó.
• Điểm nào nằm trên đường phân giác của một góc thì cách đều hai cạnh của góc đó. Nói cách khác, khoảng cách từ điểm M bất kì trên đường phân giác của góc đến hai cạnh của góc là bằng nhau.

Công thức viết phương trình đường phân giác của góc tạo bởi 2 đường thẳng

Công thức viết phương trình đường phân giác của góc tạo bởi 2 mặt phẳng như sau:

Cho 2 đường thẳng: d1: A1x + B1y + C1 = 0 và đường thẳng d2: A2x + B2y + C2 = 0

Phương trình phân giác của 2 đường thẳng này sẽ được viết như sau:

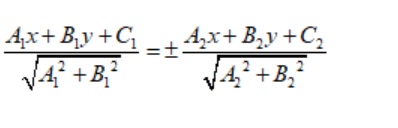
Lưu ý : Cho đường thẳng d: ax + by + c = 0 và hai điểm A( Xa; Ya) và B( Xb;Yb) hai điểm này không thuộc d

Cho f( x;y) = ax + by + c

• Nếu f( Xa;Ya). f(Xb;Yb) > 0 thì A và B sẽ nằm cùng phía với d
• Nếu f(Xa;Ya). F(Xb;Yb) < 0 thì A và B sẽ nằm khác phía với d

Các dạng bài tập phương trình đường phân giác của góc tạo bởi 2 đường thẳng

Hãy xem những bài tập minh họa về phương trình đường phân giác của góc tạo bởi 2 mặt phẳng để có thể áp dụng những bài tập khác dễ dàng hơn.

Bài tập 1

Cho đường thẳng d: 3x + 4y – 5 = 0 và 2 điểm A( 1; 3) ; B( 2; m) . Tìm m để A và B nằm cùng phía đối với d?

lời giải:

Để cho A và B nằm cùng phía đối với d khi :

Cho f( x;y) = ax + by + c

Nếu f( Xa;Ya). f(Xb;Yb) > 0 thì A và B sẽ nằm cùng phía với d

Và được trả lời như sau: ( 3 + 12 - 5)( 6 + 4m - 5) < 0 hay m > - ¼

=> đáp án : m> -¼

Bài tập 2

Cho hai đường thẳng d1: x + 2y + 3 = 0 và d2: 2x + y + 3 = 0. Viết phương trình các đường phân giác của các góc tạo bởi d1 và d2.

Lời giải

Áp dụng công thức như sau:

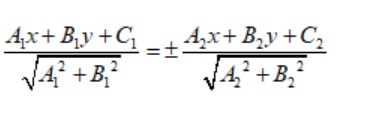
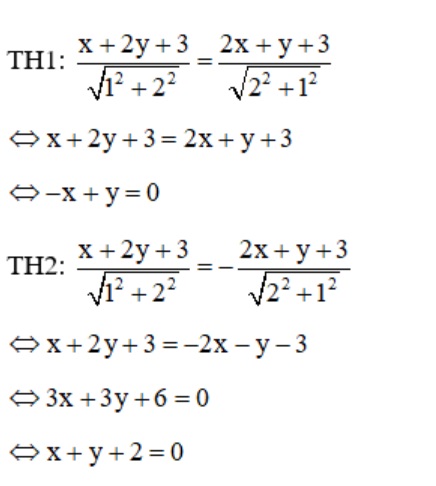
Bài tập 3

Hãy xác định cặp đường thẳng nào là phân giác của các góc hợp bởi hai đường thẳng ∆ 1 : x + 2y - 3 = 0 và ∆ 2 : 2x – y + 3 = 0.

Lời giải

Gọi N(x;y) là điểm trên đường phân giác của hai đường thẳng đã cho.

=> d(N;∆ 1) = d(N;∆ 2) =>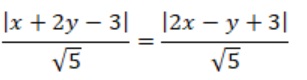

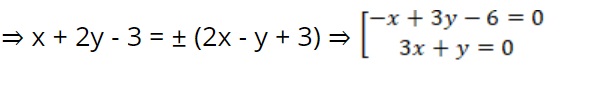
Bài tập 4

Hãy viết phương trình của các đường phân giác của các góc được tạo ra bởi hai đường thẳng d: x - 2y + 1 = 0 và d': 2x - y + 2 = 0.

Lời giải

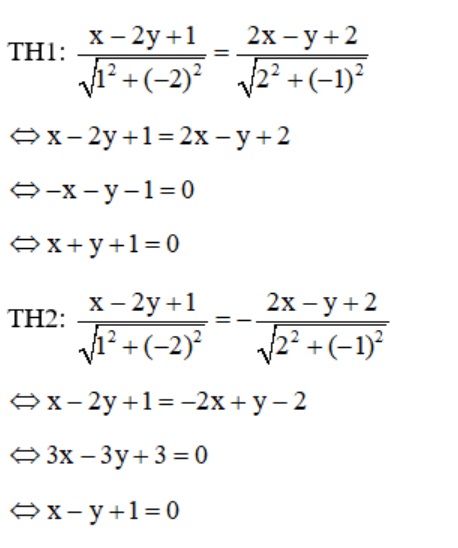
Các phương trình của đường phân giác của các góc được tạo ra bởi hai đường thẳng d và d’ là X + Y + 1 = 0 và X - Y + 1=0

Bài tập 5

Tam giác ABC có hai đỉnh B và C nằm trên trục Ox. Phương trình đường thẳng AB là 2x - y + 4 = 0 và đường thẳng AC là x - 2y - 6 = 0. Tìm phương trình đường thẳng phân giác ngoài của góc BAC.

Lời giải

Hai điểm B và C nằm trên trục Ox với tọa độ lần lượt là (-2; 0) và (6; 0). Điểm M có tọa độ (x; y) thuộc đường phân giác của góc BAC.

=> d(M, AB) = d(M, AC) ⇔ 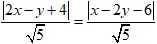⇔ |2x - y + 4| = |x - 2y - 6|

=>

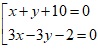
Để xác định vị trí của hai điểm B và C đối với đường thẳng x + y + 10 = 0,

Ta tính giá trị của biểu thức (-2 + 0 + 10).( 6 + 0 + 10). Kết quả cho biết hai điểm B và C cùng nằm về một phía so với đường thẳng x + y + 10 = 0.

Vì vậy, có thể kết luận rằng đường thẳng x + y + 10 = 0 là đường phân giác ngoài của góc BAC.

Bài tập 6

Viết phương trình phân giác ngoài của góc BAC của tam giác ABC, trong đó cạnh AB nằm trên đường thẳng d có phương trình 2x - y + 4 = 0, cạnh AC nằm trên đường thẳng d’ có phương trình x - 2y - 6 = 0 và hai điểm B, C đều nằm trên trục Ox.

Lời giải

Phương trình phân giác ngoài của góc BAC được tính như sau:

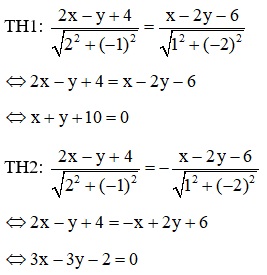
Hai điểm B và C có tọa độ là B(-2; 0) và C(6; 0) tương ứng thuộc đường thẳng Ox và d’ trên mặt phẳng. Cần xác định vị trí của hai điểm B và C liên quan đến đường thẳng x + y + 10 = 0.

Có thể suy ra từ việc (-2 + 0 + 10).( 6 + 0 + 10) > 0, hai điểm B và C nằm cùng phía so với đường thẳng x + y + 10 = 0.

Vì vậy, đường thẳng x + y + 10 = 0 được coi là đường phân giác ngoài của góc BAC.

Bài tập 7

Có hai đường thẳng d và d’ có phương trình lần lượt là x + 2y + 3 = 0 và 2x + y + 3 = 0. Yêu cầu tìm phương trình của các đường phân giác của các góc được tạo bởi hai đường thẳng này.

Lời giải

Công thức để tính đường phân giác của các góc tạo bởi hai đường d và d’ được trình bày như sau:

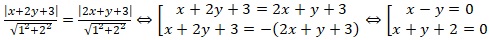
Phương trình của hai đường phân giác d và d’ là x - y = 0 và x + y + 2 = 0.

Kết luận

Trên đây là cách lập Phương trình đường phân giác của góc tạo bởi 2 đường thẳng và một số bài tập minh họa muốn gửi đến các bạn học sinh. Hãy bỏ túi những công thức hay để có thể áp dụng vào những bài tập khó nhằn hơn. Đừng quên truy cập vào Thayphu để có thể học hỏi được thêm nhiều bài toán hay nhé!