Khái niệm hàng và lớp toán lớp 4 và bài tập áp dụng

Khái niệm hàng và lớp toán lớp 4 được hiểu là mỗi hàng sẽ ứng với một lớp khác nhau. Hãy cùng chúng tôi tìm hiểu về định nghĩa, ví dụ và bài tập áp dụng nhé.

Trong hệ thống số, mỗi chữ số từ 0 đến 9 chiếm một hàng tương ứng với một đơn vị cụ thể. Ví dụ, hàng đơn vị biểu diễn các số từ 1 đến 9, hàng chục biểu diễn các số từ 10 đến 90, hàng trăm biểu diễn các số từ 100 đến 900, và hàng ngàn biểu diễn các số từ 1.000 đến 9.000.

Các hàng này được nhóm thành các lớp dựa trên đơn vị. Cụ thể, lớp đơn vị gồm hàng đơn vị, lớp chục gồm hàng chục, lớp trăm gồm hàng trăm, và lớp ngàn gồm hàng ngàn. Hiểu rõ mối quan hệ giữa hàng và lớp sẽ giúp chúng ta thành thạo các thao tác toán học như đọc, viết, so sánh và tính toán với các số. Trong bài viết này của thayphu chúng ta sẽ tìm hiểu sâu hơn về các khái niệm hàng và lớp toán lớp 4 hiểu được ý nghĩa và vai trò của chúng trong hệ thống số.

Định nghĩa của hàng và lớp toán trong toán học lớp 4

Định nghĩa của chúng trong toán học lớp 4 như sau:

Hàng (Place Value)

Trong hệ thống số, mỗi chữ số từ 0 đến 9 chiếm một hàng tương ứng với một đơn vị cụ thể. Các hàng bao gồm:

• Hàng đơn vị: Biểu diễn các số từ 1 đến 9.
• Hàng chục: Biểu diễn các số từ 10 đến 90.
• Hàng trăm: Biểu diễn các số từ 100 đến 900.
• Hàng ngàn: Biểu diễn các số từ 1.000 đến 9.000.

Các hàng tiếp theo là hàng triệu, hàng tỷ, v.v.

Lớp (Place Value Class)

Các hàng được nhóm thành các lớp dựa trên đơn vị. Các lớp bao gồm:

• Lớp đơn vị: Gồm hàng đơn vị.
• Lớp chục: Gồm hàng chục.
• Lớp trăm: Gồm hàng trăm.
• Lớp ngàn: Gồm hàng ngàn.

Các lớp tiếp theo là lớp triệu, lớp tỷ, v.v.

Ví dụ, trong số 2.345, ta có:

• Hàng đơn vị: 5
• Hàng chục: 4
• Hàng trăm: 3
• Hàng ngàn: 2
• Lớp đơn vị: 5
• Lớp chục: 4
• Lớp trăm: 3
• Lớp ngàn: 2

Tính chất và đặc điểm của hàng và lớp

Tính chất và đặc điểm của chúng trong toán học được hiểu như sau:

Tính chất và đặc điểm của hàng

• Giá trị: Mỗi hàng biểu diễn một giá trị cụ thể (từ 0 đến 9).
• Trật tự: Các hàng được xếp theo trật tự từ hàng đơn vị đến hàng lớn nhất.
• Vị trí: Vị trí của mỗi chữ số trong số quyết định giá trị của hàng.
• Căn cứ: Hàng được căn cứ vào hệ thống đếm dựa trên số 10 (hệ thập phân).

Tính chất và đặc điểm của lớp

• Đơn vị: Các lớp được xác định dựa trên đơn vị, như đơn vị, chục, trăm, ngàn, triệu, tỷ, v.v.
• Phân cấp: Các lớp được sắp xếp theo cấp bậc từ thấp đến cao.
• Mối quan hệ: Mỗi lớp cao hơn lớp trước gấp 10 lần.
• Tính chính xác: Lớp giúp chúng ta thực hiện các phép tính toán một cách chính xác.
• Đọc và viết: Lớp giúp chúng ta đọc và viết các số một cách rõ ràng và dễ hiểu.

Tổng hợp cách đọc và viết về khái niệm hàng và lớp toán lớp 4

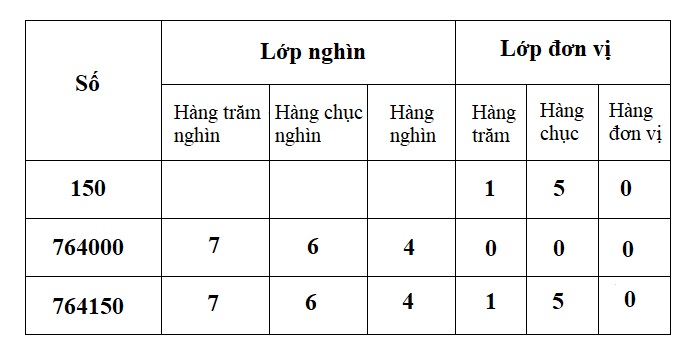
Tổng hợp cách đọc và viết giữa những hàng , lớp

Dưới đây chúng tôi đã tổng hợp những cách đọc và viết mà bạn có thể tham khảo

Cách đọc giữa những hàng, lớp

Đọc theo hàng:

• Bước 1: Bắt đầu từ hàng đầu tiên.
• Bước 2: Đọc các phần tử trong hàng đó từ trái sang phải.
• Bước 3: Sau khi đọc xong hàng đầu tiên, chuyển sang hàng thứ 2.
• Bước 4: Lặp lại bước 2, đọc các phần tử trong hàng thứ 2 từ trái sang phải.
• Bước 5: Tiếp tục chuyển sang các hàng tiếp theo và lặp lại bước 2 cho đến khi đọc hết tất cả các hàng.

Ví dụ :

1 2 3

4 5 6

7 8 9

Đọc theo hàng sẽ là: một hai ba , bốn năm sáu , bảy tám chín

Đọc theo lớp:

• Bước 1: Bắt đầu từ lớp đầu tiên (cột đầu tiên).
• Bước 2: Đọc các phần tử trong lớp đó từ trên xuống dưới.
• Bước 3: Sau khi đọc xong lớp đầu tiên, chuyển sang lớp thứ 2.
• Bước 4: Lặp lại bước 2, đọc các phần tử trong lớp thứ 2 từ trên xuống dưới.
• Bước 5: Tiếp tục chuyển sang các lớp tiếp theo và lặp lại bước 2 cho đến khi đọc hết tất cả các lớp.

Ví dụ:

1 2 3

4 5 6

7 8 9

Đọc theo lớp sẽ là: một bốn bảy, hai năm tám, ba sáu chín

Cách viết giữa những hàng, lớp

Viết theo hàng:

• Bước 1: Bắt đầu từ hàng đầu tiên.
• Bước 2: Viết các phần tử trong hàng đó từ trái sang phải, cách nhau bằng một khoảng trắng.
• Bước 3: Sau khi viết xong hàng đầu tiên, chuyển xuống hàng thứ 2.
• Bước 4: Lặp lại bước 2, viết các phần tử trong hàng thứ 2 từ trái sang phải, cách nhau bằng một khoảng trắng.
• Bước 5: Tiếp tục chuyển sang các hàng tiếp theo và lặp lại bước 2 cho đến khi viết hết tất cả các hàng.

Ví dụ:

1 2 3

4 5 6

7 8 9

Đáp án: 123, 456, 789

Viết theo lớp:

• Bước 1: Bắt đầu từ lớp đầu tiên (cột đầu tiên).
• Bước 2: Viết các phần tử trong lớp đó từ trên xuống dưới, cách nhau bằng một khoảng trắng.
• Bước 3: Sau khi viết xong lớp đầu tiên, chuyển sang lớp thứ 2.
• Bước 4: Lặp lại bước 2, viết các phần tử trong lớp thứ 2 từ trên xuống dưới, cách nhau bằng một khoảng trắng.
• Bước 5: Tiếp tục chuyển sang các lớp tiếp theo và lặp lại bước 2 cho đến khi viết hết tất cả các lớp.

Ví dụ:

1 4 7

2 5 8

3 6 9

Đáp án: 123, 456, 789

Bảng chuyển đổi giữa hàng và lớp

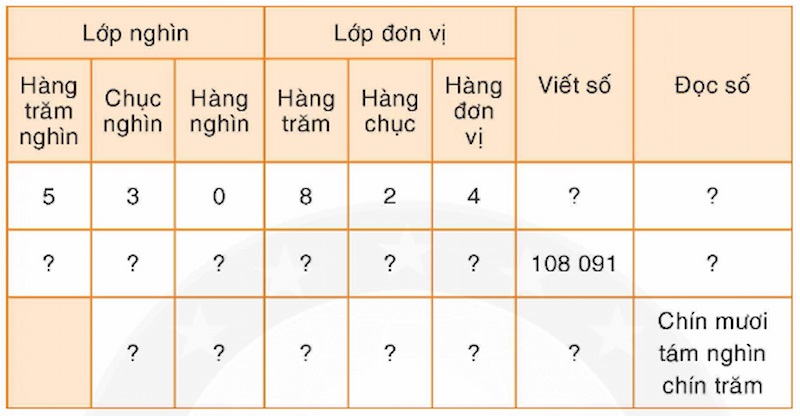
Bảng chuyển đổi giữa những hàng ứng với mỗi lớp

Để chuyển đổi giữa chúng qua lại với nhau bạn có thể sử dụng các công thức sau:

Chuyển đổi từ hàng sang lớp

Công thức: Lớp = 10^(Số hàng - 1)

Ví dụ:

• Hàng đơn vị (1) → Lớp = 10^(1-1) = 1 (Đơn vị)
• Hàng trăm (3) → Lớp = 10^(3-1) = 100 (Trăm)
• Hàng triệu (6) → Lớp = 10^(6-1) = 1.000.000 (Triệu)

Chuyển đổi từ lớp sang hàng

Công thức: Số hàng = Số chữ số trong lớp

Ví dụ:

• Lớp Đơn vị (1) → Số hàng = 1
• Lớp Trăm (100) → Số hàng = 3
• Lớp Triệu (1.000.000) → Số hàng = 6

Những dạng bài tập về hàng và lớp

Dưới đây chúng tôi đã tổng hợp những dạng thường hay gặp về những hàng ứng với mỗi lớp

Dạng 1: Xác định lớp của một số

Cách giải: Đếm số chữ số trong số đó và áp dụng công thức Lớp = 10^(Số hàng - 1)

Ví dụ: Xác định lớp của số 456.789.012.

Đáp án: 456.789.012 có 9 chữ số, nên lớp từ Đơn vị đến Tỷ.

Dạng 2: Xác định số hàng của một số

Cách giải: Đếm số chữ số trong số đó và áp dụng công thức Số hàng = Số chữ số trong lớp

Ví dụ: Xác định số hàng của số 678.901.234.567.

Đáp án: 678.901.234.567 có 12 hàng, từ Đơn vị đến Nghìn tỷ.

Dạng 3: Tính tổng các hàng của một số

Cách giải: Tách số thành các hàng, rồi cộng tổng các hàng lại

Ví dụ: Tính tổng các hàng của số 98.765.432.

Đáp án: 98.765.432 có 8 hàng, tổng các hàng là 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 = 44.

Dạng 4: Tìm số có lớp cho trước

Cách giải: Sử dụng công thức Lớp = 10^(Số hàng - 1) để tìm số có lớp cụ thể

Ví dụ: Tìm số có lớp Trăm nghìn.

Đáp án: 100.000, 200.000, 300.000, ..., 900.000.

Dạng 5: Tìm số có số hàng cho trước

Cách giải: Sử dụng công thức Số hàng = Số chữ số trong lớp để tìm số có số hàng cụ thể

Ví dụ: Tìm số có 6 hàng.

Đáp án: 1.000.000, 10.000.00, 100.000.00, 1.000.000.000, 10.000.000.000, 100.000.000.000.

Dạng 6: Thực hiện phép tính với các số lớn

Cách giải: Thực hiện phép tính như bình thường, chú ý đến việc đổi đơn vị

Ví dụ: Tính 456.789.012 + 678.901.234.

Đáp án: 1.135.690.246.

Dạng 7: Chuyển đổi từ số thập phân sang số hàng và lớp

Cách giải: Tách số thập phân thành các hàng và lớp tương ứng

Ví dụ: Chuyển số 123.456 từ số thập phân sang số hàng và lớp.

Đáp án: 123 hàng đơn vị, lớp trăm;

0.456 hàng phần thập phân, lớp phần trăm.

Dạng 8: Chuyển đổi từ số hàng và lớp sang số thập phân

Cách giải: Kết hợp các hàng và lớp để tạo thành số thập phân

Ví dụ: Chuyển số 789 hàng đơn vị, lớp trăm; 0.45 hàng phần thập phân, lớp phần trăm sang số thập phân.

Đáp án: 789.45

Dạng 9: Tính tổng các lớp của một số

Cách giải: Tách số thành các lớp, rồi cộng tổng các lớp lại

Ví dụ: Tính tổng các lớp của số 12.345.678.

Đáp án: 12 (Triệu) + 3 (Ngàn) + 4 (Trăm) + 5 (Chục) + 6 (Đơn vị) + 7 (Phần trăm) + 8 (Phần nghìn) = 12.345.678

Dạng 10: Tính tổng các hàng và lớp của một số

Cách giải: Tách số thành các hàng và lớp, rồi cộng tổng các hàng và lớp lại

Ví dụ: Tính tổng các hàng và lớp của số 987.654.321.

Đáp án: 9 (Tỷ) + 8 (Trăm triệu) + 7 (Chục triệu) + 6 (Triệu) + 5 (Ngàn) + 4 (Trăm) + 3 (Chục) + 2 (Đơn vị) + 1 (Phần trăm) = 987.654.321

Một số lưu ý khi giải bài tập hàng và lớp

Dưới đây chúng tôi đã tổng hợp một số lưu ý khi giải bài tập về hàng, lớp:

Xác định kích thước (số hàng, số cột) của ma trận

Số hàng thể hiện số dòng của ma trận.

Số cột thể hiện số cột của ma trận.

Tính toán các phép toán cơ bản trên ma trận

Tổng các phần tử trong hàng/cột.

Tìm giá trị lớn nhất/nhỏ nhất trong hàng/cột.

Tính tổng các phần tử trên đường chéo chính/phụ.

Nắm vững các định nghĩa và tính chất của các loại ma trận

Ma trận đơn vị.

Ma trận chuyển vị.

Ma trận nghịch đảo.

Ma trận đối xứng.

Bài tập áp dụng

Câu 1: Cho ma trận A = [1 2 3; 4 5 6; 7 8 9]. Số hàng của ma trận A là:

A. 2

B. 3

C. 4

D. 5

Đáp án: B. 3

Câu 2: Tổng các phần tử trong hàng thứ 2 của ma trận A = [1 2 3; 4 5 6; 7 8 9] là:

A. 12

B. 15

C. 18

D. 21

Đáp án: B. 15

Câu 3: Phần tử lớn nhất trong cột thứ 3 của ma trận A = [1 2 3; 4 5 6; 7 8 9] là:

A. 3

B. 6

C. 9

D. 12

Đáp án: C. 9

Câu 4: Tổng các phần tử trên đường chéo chính của ma trận vuông A = [1 2 3; 4 5 6; 7 8 9] là:

A. 12

B. 15

C. 18

D. 21

Đáp án: B. 15

Câu 5: Ma trận đơn vị kích thước 4x4 có dạng:

A. [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]

B. [0 0 0 0; 0 0 0 0; 0 0 0 0; 0 0 0 0]

C. [1 1 1 1; 1 1 1 1; 1 1 1 1; 1 1 1 1]

D. [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

Đáp án: A. [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]

Câu 6: Ma trận chuyển vị của ma trận A = [1 2 3; 4 5 6; 7 8 9] là:

A. [1 4 7; 2 5 8; 3 6 9]

B. [1 2 3; 4 5 6; 7 8 9]

C. [1 2; 3 4; 5 6]

D. [7 8 9; 4 5 6; 1 2 3]

Đáp án: A. [1 4 7; 2 5 8; 3 6 9]

Câu 7: Tích của ma trận A = [1 2; 3 4] và ma trận B = [5 6; 7 8] là:

A. [19 22; 43 50]

B. [12 16; 28 40]

C. [26 30; 58 66]

D. [7 10; 15 22]

Đáp án: A. [19 22; 43 50]

Câu 8: Ma trận nghịch đảo của ma trận A = [1 2; 3 4] là:

A. [0.4 -0.2; -0.6 0.4]

B. [0.5 0.25; 0.75 0.5]

C. [2 -1; -1.5 1]

D. [1 0; 0 1]

Đáp án: A. [0.4 -0.2; -0.6 0.4]

Câu 9: Định thức của ma trận A = [1 2; 3 4] là:

A. 0

B. 1

C. 2

D. -2

Đáp án: D. -2

Câu 10: Ma trận A = [1 2 3; 2 4 5; 3 5 6] là ma trận đối xứng:

A. Đúng

B. Sai

Đáp án: A. Đúng

Trên đây thayphu.net đã tổng hợp những lý thuyết về khái niệm hàng và lớp môn toán lớp 4 cũng như bài tập về hàng , lớp hi vọng các em đã nắm vững lý thuyết và kỹ năng này và nếu còn bất kì câu hỏi nào xin liên hệ chúng tôi nhé