Hình lăng trụ đứng tam giác lớp 7, lý thuyết & bài tập
Kiến thức về hình lăng trụ đứng tam giác lớp 7 và cách áp dụng để giải bài tập. Tổng hợp các dạng bài thường gặp và lời giải chi tiết.
Hình lăng trụ đứng tam giác lớp 7 là một phần nội dung cơ bản trong chương trình Toán hình lớp 7. Để làm tốt các dạng bài tập các em cần nắm vững công thức tính diện tích, thể tích. Hãy cùng thayphu ôn tập lại các lý thuyết cơ bản này nhé!
Lý thuyết hình lăng trụ đứng tam giác lớp 7
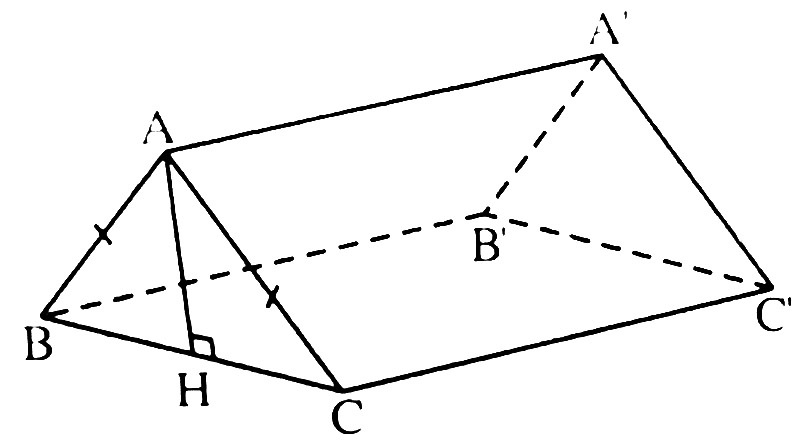
Trong hình lăng trụ đứng tam giác sẽ có 2 mặt đáy song song với nhau, các mặt bên là những hình chữ nhật. Và các cạnh bên song song, bằng nhau. Độ dài của 1 cạnh bên được gọi là chiều cao của lăng trụ đứng.
Ví dụ: Cho hình lăng trụ đứng tam giác ABC A’B’C’ ta có:
- Các đỉnh lần lượt là A, B, C, A’, B’, C’
- Các cạnh đáy lần lượt là AB, BC, AC,A’B’,B’C’, A’C’
- Các cạnh bên lần lượt là AA’, BB’, CC’
- Các mặt bên đó là các hình chữ nhật ABA’B’, ACA’C’, BCB’C’
- 2 mặt đáy đó là các tam giác ABC, A’B’C’
Tạo lập hình lăng trụ đứng tam giác lớp 7
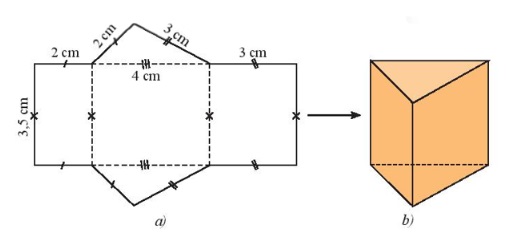
Để tạo lập một hình lăng trụ đứng tam giác với kích thước của 3 cạnh đáy lần lượt là 2cm, 3cm, 4cm và chiều cao là 3,5cm.
Ta thực hiện các bước như sau:
-
Trên 1 tấm bìa ta vẽ 3 hình chữ nhật và 2 tam giác có kích thước như hình a. Sau đó cắt miếng bìa như hình rồi gấp theo các đường nét đứt. Cuối cùng ta sẽ được hình lăng trụ đứng tam giác như hình b.
Diện tích xung quanh và thể tích hình lăng trụ đứng tam giác lớp 7
Công thức tính diện tích xung quanh của lăng trụ đứng tam giác đó là:
Sxq = C.h
Công thức tính thể tích lăng trụ đứng tam giác là:
V = Sđáy . h
Trong đó:
- Với Sxq - Diện tích xung quanh lăng trụ đứng
- V - Thể tích lăng trụ đứng
- C - Chu vi 1 đáy của hình lăng trụ đứng
- S đáy - Diện tích 1 đáy của hình lăng trụ đứng
- h - Chiều cao của lăng trụ đứng đó
Công thức tính diện tích toàn phần đó là:
Stp = Sxq + 2S đáy
Các dạng bài tập về hình lăng trụ đứng tam giác lớp 7
Sau đây là 2 dạng bài tập cơ bản về hình lăng trụ đứng tam giác, các em học sinh lớp 7 cùng tham khảo:
Dạng 1 - Nhận biết các yếu tố liên quan hình lăng trụ đứng tam giác
Phương pháp giải: Đầu tiên là vẽ hình, quan sát để xác định các mặt, các cạnh và các đỉnh. Tiến hành vẽ hình lăng trụ đứng bằng cách vẽ 1 đáy rồi vẽ các cạnh bên là các đoạn thẳng song song và bằng nhau.
Bài tập 1
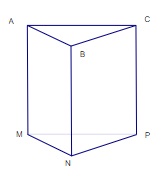
Cho hình lăng trụ đứng tam giác như hình vẽ bên dưới. Hãy quan sát và gọi tên các đỉnh, các mặt đáy, mặt bên, cạnh đáy, cạnh bên của hình.
Lời giải:
- Hình lăng trụ đứng tam giác ABC.MNP có các đỉnh là A, B, C, M, N, P
- Hình lăng trụ đứng tam giác ABC.MNP có các cạnh đáy là AB, AC, BC, MN, MP, NP
- Hình lăng trụ đứng tam giác ABC.MNP có các cạnh bên là AM, BN, CP
- Hình lăng trụ đứng tam giác ABC.MNP có các mặt đáy là các tam giác ABC, MNP
- Hình lăng trụ đứng tam giác ABC.MNP có các mặt bên là các hình chữ nhật ABNM, BCPN, ACPM.
Bài tập 2
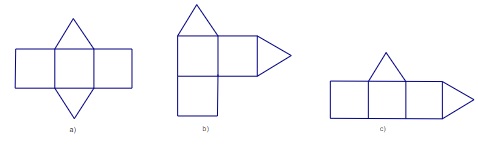
Trong các hình khai triển bên dưới đây, hình nào khi gấp lại sẽ được một hình lăng trụ đứng?
Lời giải:
Hình khai triển a sau khi gấp lại sẽ hình thành được 1 hình lăng trụ đứng tam giác.
Bài tập 3
Cho hình lăng trụ đứng tam giác như bên dưới:
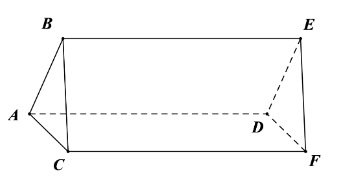
- Hãy chỉ ra các mặt đáy và mặt bên của hình lăng trụ đứng tam giác đó
- Tìm xem những cạnh nào có độ dài bằng với cạnh AD?
Lời giải:
-
2 mặt đáy của hình lăng trụ đứng là tam giác ABC và tam giác DEF
Các mặt bên lần lượt là các hình chữ nhật ABED, BCFE, ACFD.
-
Xét hình lăng trụ đứng tam giác ABCDEF có các mặt bên đều là các hình chữ nhật ABED, ACFD.
Từ đó suy ra AD = BE, AD = CF
Kết luận các cạnh có độ dài bằng với cạnh AD đó là BE và CF.
Dạng 2 - Tìm diện tích và thể tích của hình lăng trụ đứng tam giác
Phương pháp giải: Áp dụng các công thức tính diện tích xung quanh (Sxq = C.h), công thức tính diện tích toàn phần (Stp = Sxq + 2Sđáy), công thức tính thể tích (V = Sđáy . h)
Bài tập 1
Cho một hình lăng trụ đứng ABCA’B’C’, mặt đáy ABC là tam giác vuông cân có AB = AC = 3cm và BC = 5cm, AA’ = 4cm. Hãy tính diện tích xung quanh và thể tích của hình lăng trụ.
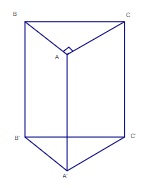
Lời giải:
Chu vi của tam giác ABC là AB + AC + BC = 3 + 3 + 5 = 11 cm
Diện tích xung quanh của hình lăng trụ ABC A’B’C’ là:
Sxq = C.h = 11.4 = 44 (cm2)
Diện tích của tam giác ABC là:
SABC = ½ AB. AC = ½ 3. 3 = 9/2 (cm2)
Thể tích của hình lăng trụ đứng ABC A’B’C’ là:
V = SABC. h = 9/2 . 4 = 18 cm3
Bài tập 2
Cho tấm lịch để bàn có dạng là 1 hình lăng trụ đứng, ACB là tam giác cân ở C. Hãy tính diện tích của miếng bìa để làm 1 tấm lịch như trên.
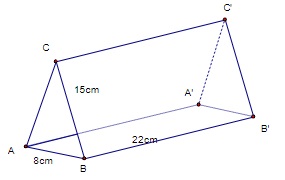
Lời giải:
Theo đề ra tam giác ACB cân tại C nên ta có: CA = CB = 15cm
Chu vi của tam giác ACB là:
C = 8 + 15 + 15 = 38 cm
Diện tích của miếng bìa để làm tấm lịch đó là diện tích xung quanh của hình lăng trụ đứng. Ta có:
Sxq = C.h = C.BB’ = 38 . 22 = 836 cm2
Kết luận diện tích miếng bìa để làm tấm lịch đó là 836 cm2.
Bài tập 3
Cho 1 lăng trụ đứng ABC DEF có mặt đáy là tam giác vuông ABC vuông tại A. Biết rằng chiều của hình lăng trụ là 9 cm và độ dài 2 cạnh góc vuông của đáy là 3 cm, 4 cm, cạnh huyền có độ dài là 5 cm.
- Hãy tính diện tích xung quanh của lăng trụ đứng đó
- Hãy tính diện tích toàn phần của lăng trụ đứng đó
- Hãy tính thể tích của lăng trụ đứng đó
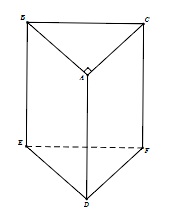
Lời giải:
-
Đầu tiên ta tìm chu vi của tam giác ABC
Chu vi của tam giác ABC sẽ là:
3 + 4 + 5 = 12 cm
Diện tích xung quanh của hình lăng trụ đứng tam giác ABC DEF là:
Sxq = 2p.h = 12. 9 = 108 (cm2)
-
Để tính diện tích toàn phần của lăng trụ ta tìm diện tích tam giác ABC.
Diện tích của tam giác ABC là:
SABC = ½ AB.AC = ½ 3.4 = 6 (cm2)
Diện tích toàn phần của hình lăng trụ đứng ABC DEF là
Stp = Sxq + 2S ABC = 108 + 2.6 = 120 cm2
-
Thể tích của hình lăng trụ đứng ABC DEF là:
V = SABC . h = 6.9 = 54 cm3
Bài tập tự luyện
Bài 1: Cho một hình lăng trụ đều ABC A’B’C’ với AB = 4cm, AA’ = 4cm. Hãy tính diện tích xung quanh và thể tích của hình lăng trụ đó.
Bài 2: Cho một chiếc lều có dạng là hình lăng trụ đứng có đáy là tam giác. Biết rằng thể tích phần không gian bên trong là 2,16cm3 và chiều dài CC’ của lều là 2,4m; chiều rộng BC là 1,2m. Hãy tính chiều cao của chiếc lều.
Bài 3: Cho hình lăng trụ đứng ABC A’B’C’ biết chiều cao là 5m, có đáy là tam giác vuông tại A và AB = 2m, thể tích của hình lăng trụ là 15m3. Hãy tính độ dài của cạnh AC.
Trên đây là tổng hợp các lý thuyết, công thức tính diện tích và thể tích của hình lăng trụ đứng tam giác lớp 7. Các em cùng tham khảo các dạng bài tập và phương pháp giải chi tiết để vận dụng làm bài. Để cập nhật thêm các bài học Toán lớp 7 hữu ích hãy truy cập ngay vào mục Toán 7 của thayphu.net nhé!


 Định nghĩa góc giữa hai đường thẳng
Định nghĩa góc giữa hai đường thẳng  Góc giữa hai vectơ
Góc giữa hai vectơ  Định lý cosin
Định lý cosin 