Hệ phương trình bậc nhất ba ẩn, lý thuyết và bài tập áp dụng

Định nghĩa, tính chất cùng các phương pháp giải toán liên quan đến hệ phương trình bậc nhất ba ẩn, các dạng bài tập vận dụng giúp bạn học rèn luyện thêm.

Trong chương trình toán lớp 10, hệ phương trình bậc nhất ba ẩn là kiến thức bạn học cần nắm vững để có thể vững vàng hơn ở khối lượng kiến thức về sau. Dưới đây là những kiến thức cơ bản kèm theo những dạng bài thường ra giúp bạn củng cố sau bài học. Cùng thayphu tìm hiểu kĩ hơn tại thayphu.net nhé!

Lý thuyết phương trình bậc nhất ba ẩn cần nắm:

Để có thể giải được các dạng toán xoay quanh hệ phương trình bậc nhất ba ẩn thì bạn học cần nắm được những lý thuyết liên quan bao gồm định nghĩa về phương trình bậc nhất ba ẩn cũng như định nghĩa về hệ phương trình.

Định nghĩa về phương trình bậc nhất ba ẩn:

Phương trình bậc nhất ba ẩn là hệ thức được viết dưới dạng: ax + by + cz = d. Trong đó x, y, z lần lượt là 3 ẩn và các hệ số a, b, c cho trước không được đồng thời bằng 0 ( Vì khi các hệ số bằng 0 thì phương trình vô nghiệm )

Nghiệm thỏa mãn của phương trình bậc nhất ba ẩn là ( x0, y0, z0 ) nếu các nghiệm thay thế vào phương trình ax + by + cz = d và trở thành mệnh đề đúng x=x0, y=y0, z=z0.

Định nghĩa về hệ phương trình bậc nhất ba ẩn:

Hệ phương trình bậc nhất ba ẩn là hệ phương trình mà mỗi phương trình trong hệ là một phương trình bậc nhất với ba ẩn đó.

Đối với hệ phương trình bậc nhất ba ẩn 3 ẩn lần lượt là x, y, z và các hệ số a, b, c trong mỗi phương trình không đồng thời bằng 0.

Bộ số ( x0, y0, z0 ) đồng thời nghiệm đúng tất cả các phương trình của một hệ phương trình bậc nhất ba ẩn được gọi là nghiệm của hệ phương trình đó.

Hệ phương trình bậc nhất ba ẩn được viết dưới dạng:

• a1x+bay+c1z=d1
• a2x+b2y+c2z=d2
• a3x+b3y+c3z=d3

Hệ phương trình bậc nhất ba ẩn

Một số nhận xét về hệ phương trình

Cho 2 hệ phương trình như dưới đây:

a1x+bay+c1z=d1 a1x+bay+c1z=d1

(I) a2x+b2y+c2z=d2 (II) a2x+b2y+c2z=d2

a3x+b3y+c3z=d3 a3x+b3y+c3z=d3

Nếu tập nghiệm của phương trình (I) bằng nghiệm của phương trình (II) thì 2 phương trình này được gọi là tương đương. Được biểu thị bằng dấu

Phép biến đổi hệ phương trình bậc nhất ba ẩn về hệ phương trình tương đương với nó được gọi là phép biến đổi tương đương hệ phương trình bậc nhất ba ẩn.

Ví dụ về phương trình bậc nhất ba ẩn và hệ phương trình bậc nhất ba ẩn

Ví dụ: Hệ phương trình nào dưới đây là hệ phương trình bậc nhất ba ẩn. Bộ số ( 2, 4, -6 ) có phải là nghiệm thỏa mãn của phương trình hay không.

1. 2x + 3y - 5z = 13

4x - 2y - 3z = 3

-x + 5y - 4z2= 5

2. -2x + y + z = 3

5x + y - 3z = 16

x+ 2y = 5

Lời giải:

Hệ phương trình bậc nhất ba ẩn là hệ phương trình b. Vì hệ phương trình a tại phương trình thứ ba có ẩn mũ hai.

Thay x=2, y=4, z=-6 ta được : -2.(2) + 4 + (-6) = 3

5.(2) + 4 - 3(-6) = 16

2+ 2.(4) = 5

Nhận xét: Khi thay bộ ba số ( 2, 4, -6 ) thì hệ phương trình thỏa mãn.

Bộ ba số ( 2, 4, -6 ) là nghiệm của hệ phương trình đã cho.

Phương pháp Gauss giúp giải hệ phương trình bậc nhất ba ẩn

Lý thuyết về phương pháp Gauss

Để giải được phương trình bậc nhất ba ẩn, ta thường biến đổi chúng về dạng hệ phương trình đơn giản hơn, có những hệ số và ẩn có thể sử dụng phương pháp loại trừ. Dưới đây là 3 cách thường được áp dụng khi biến đổi:

• Phương pháp 1: Nhân hai vế của một phương trình trong hệ với một hệ số khác 0
• Phương pháp 2: Đổi vị trí của 2 phương trình thuộc hệ phương trình.
• Phương pháp 3: Thực hiện phép cộng mỗi vế của phương trình với vế tương ứng của phương trình khác để được phương trình mới có ẩn số ít hơn.

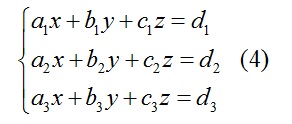
Lý thuyết về phương pháp Gauss

Bài tập áp dụng phương pháp Gauss

Ví dụ 1: Thực hiện lần lượt các yêu cầu a) b) c) và giải hệ phương trình dưới đây bằng phương pháp Gauss

x+y-2z=3

-x+y+6z=13

2x+y-9z=-5

1. Khử ẩn x có ở phương trình (II) bằng cách cộng phương trình (I) và (II)
2. Khử ẩn x có ở phương trình (III) bằng cách nhân phương trình (I) với hệ số (-2) sau đó cộng với phương trình (III). Viết phương trình (III) sau khi biến đổi , từ đó viết hệ mới lập.
3. Làm tương tự với hệ mới nhận ở câu b), khử ẩn y ở phương trình (III) bằng phương trình (II) (III).
4. Giải hệ tam giác có được từ câu a) b) c)

Lời giải:

1. Thực hiện phép cộng đối với phương trình (I) (II) ta được:

(x+y-2z)+(-x+y+6z)=3+13

2y+4z=16

y+2z=8

2. Thực hiện phép nhân phương trình (I) với hệ số (-2) sau đó cộng với phương trình (III) ta được:

-2.(x+y-2z)+(2x+y-9z)=(-2).3+(-5)

-y-5z=-11

y+5z=11

Hệ mới nhận được: x+y-2z=3

y+2z=8

y+5z=11

3. Thực hiện phép trừ giữa phương trình (II) và (III) ta được:

(y+2z)-(y+5z)=8-11

-3z=3

z=1

Hệ mới nhận được: x+y-2z=3

y+2z=8

z=1

4. Giải hệ có ở câu c)

• x+y-2z=3

y+2z=8

z=1

• x+y-2z=3

y+2.1=8

z=1

• x+y-2z=3

y=6

z=1

• x+6-2.1=3

y=6

z=1

x=-1

y=6

z=1

Vậy nghiệm của hệ phương trình đã cho trên là (-1; 6; 1)

Ví dụ 2: Giải hệ phương trình sau bằng phương pháp Gauss:

x-2y=1

x+2y-z=-2

x-3y+z=3

Lời giải:

x-2y=1

x+2y-z=-2

x-3y+z=-5

x-2y=1

-4y+z=3

x-3y+z=3

x-2y=1

-4y+z=3

y-z=-2

x-2y=1

-4y+z=3

-3z=-5

x-2y=1

-4y+5/3=3

z=5/3

x=1/3

y=-1/3

z=5/3

Vậy nghiệm của hệ phương trình đã cho trên là (⅓; -⅓; 5/3)

Kết luận

Bài viết trên là toàn bộ hệ thống kiến thức liên quan đến hệ phương trình bậc nhất ba ẩn cùng phương pháp Gauss giúp bạn học liên hệ. Với mục tiêu đem đến những nguồn kiến thức bổ ích về toán học cũng như giúp đỡ bạn học trong quá trình học toán 10. Hy vọng với những kiến thức đã cung cấp sẽ giúp bạn học tốt hơn chương trình toán 10.