Hai đường thẳng song song, tính chất, dấu hiệu và bài tập

Tập hợp các kiến thức cơ bản liên quan đến hai đường thẳng song song trong chương trình Toán lớp 7. Các dạng bài tập thường gặp và cách giải chi tiết.

Hai đường thẳng song song là gì? Làm thế nào để nhận biết 2 đường thẳng song song, chúng có tính chất gì đặc biệt? Bài viết sau đây thayphu sẽ tổng hợp đầy đủ các kiến thức cùng bài tập liên quan về nội dung này. Mời các em cùng theo dõi chi tiết!

Khái niệm về hai đường thẳng song song

Tổng hợp lý thuyết về 2 đường thẳng song song

Hai đường thẳng song song trong một mặt phẳng là hai đường thẳng không có điểm chung. Ký hiệu là a // b.

Hai đường thẳng phân biệt thì cắt nhau hoặc song song với nhau.

Dấu hiệu nhận biết hai đường thẳng song song

• Nếu 2 đường thẳng cắt 1 đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì 2 đường thẳng song song.
• Nếu 2 đường thẳng cắt 1 đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì 2 đường thẳng song song.
• Nếu 2 đường thẳng cắt 1 đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì 2 đường thẳng song song.

Ngoài ra còn có dấu hiệu là: Nếu 2 đường thẳng cắt một đường thẳng thứ 3 tạo thành 1 cặp góc so le ngoài bằng nhau thì 2 đường thẳng song song.

Ví dụ minh họa:

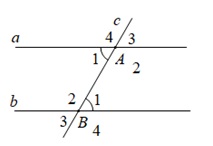
Ta có: A1 = B1 mà 2 góc này ở vị trí so le trong => a // b

A3 = B1 mà 2 góc này ở vị trí đồng vị => a // b

A2 + B1 = 180 độ mà 2 góc này ở vị trí trong cùng phía => a // b.

Tiên đề Ơ-clit về 2 đường thẳng song song: Qua 1 điểm nằm ngoài 1 đường thẳng chỉ có 1 đường thẳng song song với đường thẳng đó.

Tính chất của hai đường thẳng song song

Nếu 2 đường thẳng song song bị cắt bởi 1 đường thẳng thứ 3 thì:

• Hai góc so le trong còn lại bằng nhau
• Hai góc đồng vị bằng nhau
• Hai góc trong cùng phía bù nhau.

Ví dụ minh họa:

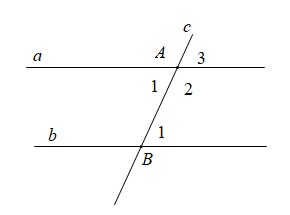
Nếu a // b thì A1 = B1, A3 = B1 và A2 + B1 = 180 độ.

Vẽ 2 đường thẳng song song

Vẽ 1 đường thẳng b đi qua điểm M và song song với đường thẳng a (M không thuộc a) bằng êke.

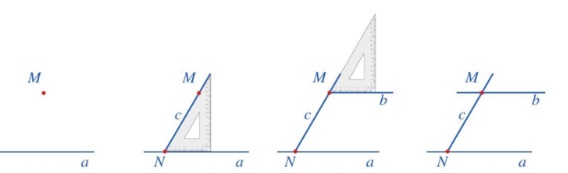
• B1: Vẽ đường thẳng a và điểm M không thuộc a
• B2: Đặt êke sao cho cạnh ngắn của góc vuông nằm trên đường thẳng a và cạnh huyền đi qua điểm M. Vẽ theo cạnh huyền 1 phần đường thẳng c đi qua điểm M (đường thẳng c cắt đường thẳng a tại điểm N).
• B3: Dịch chuyển êke sao cho cạnh huyền của êke vẫn nằm trên đường thẳng c còn cạnh ngắn của góc vuông đi qua điểm M. Vẽ theo cạnh ngắn của góc vuông 1 phần đường thẳng b đi qua điểm M.
• B4: Vẽ hoàn thiện đường thẳng b.

Nhận xét: Qua 1 điểm ở ngoài 1 đường thẳng luôn có 1 đường thẳng song song với đường thẳng đó.

Các dạng toán về hai đường thẳng song song thường gặp

Dạng 1 - Nhận biết và chứng minh 2 đường thẳng song song

Phương pháp giải:

• Xét cặp góc so le trong, cặp góc đồng vị hoặc cặp góc trong cùng phía.
• Sử dụng dấu hiệu nhận biết 2 đường thẳng song song để chứng minh.

Bài tập: Cho hình vẽ biết góc CFE = 55 độ, góc E1 = 125 độ. Hãy chứng minh AB // CD.

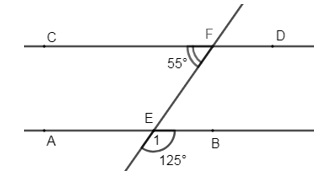
Cách giải:

Vì E1 và BEF là 2 góc kề bù (giả thiết)

=> E1 + BEF = 180 độ => BEF = 180 độ - E1 = 180 độ - 125 độ = 55 độ

=> BEF = CFE = 55 độ.

Mà BEF và CFE là 2 góc so le trong nên suy ra AB // CD (dấu hiệu nhận biết 2 đường thẳng song song).

Dạng 2 - Tính số đo góc tạo bởi đường thẳng cắt 2 đường thẳng song song

Phương pháp giải: Sử dụng tính chất của 2 đường thẳng song song.

Bài tập: Cho hình vẽ dưới đây, biết a // b. Hãy tính các góc x; y

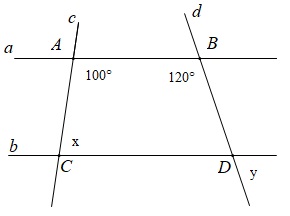
Cách giải:

Vì a // b nên BAC + ACD = 180 độ (hai góc trong cùng phía bù nhau)

=> 100 độ + x = 180 độ => x = 80 độ

Tương tự ta có: ABD + CDB = 180 độ => CDB = 60 độ.

Suy ra y = CDB = 60 độ (2 góc đối đỉnh)

Kết luận x = 80 độ và y = 60 độ.

Dạng 3 - Xác định các góc bằng nhau hoặc bù nhau dựa vào tính chất 2 đường thẳng song song.

Phương pháp giải: Đầu tiên chứng minh 2 đường thẳng song song (nếu chưa có). Sau đó sử dụng tính chất liên quan đến 2 đường thẳng song song ở trên.

Bài tập: Cho hình vẽ, biết a // b, A1 - C1 = 40 độ, hãy tính A2, C2

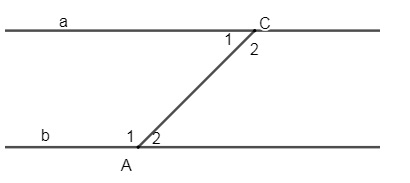
Theo đề bài ta có a // b

=> A1 + C1 = 180 độ (2 góc trong cùng phía bù nhau)

Ta lại có:

A1 - C1 = 40 độ => A1 = (180 độ + 40 độ) : 2 = 110 độ

=> C1 = 110 độ - 40 độ = 70 độ

Vì a // b => A1 = C2 = 110 độ và C1 = A2 = 70 độ (2 góc sole trong)

Vậy nên A2 = 70 độ và C2 = 110 độ.

Bài tập vận dụng

Bài tập 1

Cho hình vẽ sau đây:

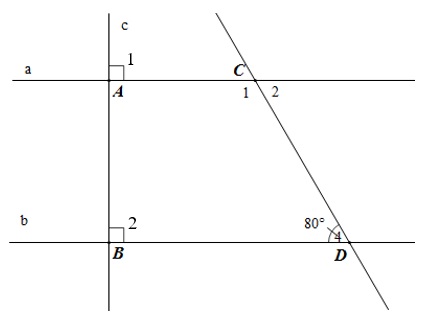
1. Vì sao a // b?
2. Tính số đo của các góc C1, C2

Cách giải:

1. Ta có góc A1 và góc B2 là 2 góc ở vị trí đồng vị, mà góc A = góc B = 90 độ.

Vậy nên a // b (dấu hiệu nhận biết).

2. Ta có C1 và D4 là 2 góc trong cùng phía.

Mà a // b nên C1 + D4 = 180 độ

=> C1 = 180 độ - D4 = 180 độ - 80 độ = 100 độ

C2 và D4 ở vị trí so le trong nên C2 = D4 = 80 độ.

Kết luận C1 = 100 độ và C2 = 80 độ.

Bài tập 2

Cho hình vẽ

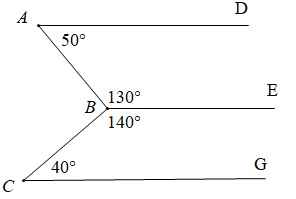
Hãy chọn phát biểu đúng:

1. AD // BE
2. BE // CG
3. Cả A, B đều sai
4. Cả A, B đều đúng.

Cách giải:

Vì A + ABE = 50 độ + 130 độ = 180 độ mà 2 góc ở vị trí trong cùng phía nên AD // BE.

Tương tự: CBE + C = 140 độ + 40 độ = 180 độ mà 2 góc ở vị trí trong cùng phía nên BE // CG.

Vậy là cả câu A, B đều đúng.

Bài tập 3

Trên đường thẳng xx’ lấy 2 điểm M và N. Trên 2 nửa mặt phẳng đối nhau bờ là xx’ lần lượt dựng các tia Ma, Nb sao cho xMa = 100 độ, bNx = 80 độ.

1. Chứng minh Ma // Nb
2. Gọi Mt và Nz lần lượt là các tia phân giác của aMx' và xNb. Tia Mt có song song với tia Nz không? Vì sao?

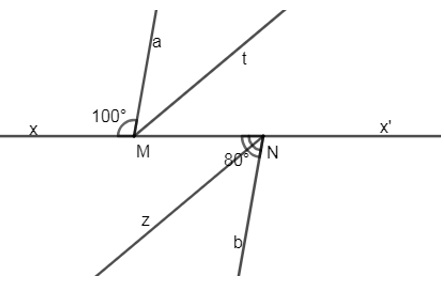
Cách giải:

1. Ta có: xMa + aMx' = 180 độ (kề bù)

=> aMx' = 180 độ - 100 độ = 80 độ

=> aMx' = xNb = 80 độ

Mà 2 góc này ở vị trí so le trong nên suy ra Ma // Nb.

2. Vì Mt là tia phân giác của aMx' (giả thiết)

=> tMx' = aMx' / 2 = 80 độ : 2 = 40 độ (tính chất tia phân giác)

Vì Nz là tia phân giác của xNb (giả thiết)

=> xNz = xNb / 2 = 80 độ : 2 = 40 độ (tính chất tia phân giác)

Mà 2 góc tMx' và xNz là 2 góc ở vị trí so le trong => Mt // Nz (dấu hiệu nhận biết).

Trên đây là tổng hợp về khái niệm, tính chất và dấu hiệu nhận biết hai đường thẳng song song. Bên cạnh đó là các dạng bài tập liên quan kèm cách giải. Chúc các em ôn tập tốt và hoàn thành các bài tập được giao nhé!