Góc nội tiếp chắn nửa đường tròn, lý thuyết & bài tập

Góc nội tiếp chắn nửa đường tròn là gì? Tổng kiến thức và các dạng bài tập cơ bản về góc nội tiếp kèm phương pháp giải hay, dễ hiểu.

Trong chương trình Toán học lớp 9, các em sẽ được làm quen với bài học về góc nội tiếp. Bài viết sau đây sẽ ôn lại các định nghĩa, hệ quả và tính chất góc nội tiếp, tìm hiểu về góc nội tiếp chắn nửa đường tròn. Và thực hành giải các dạng bài tập thường gặp nhất. Hãy cùng thayphu theo dõi ngay nhé!

Kiến thức về góc nội tiếp

Góc nội tiếp là góc có 2 cạnh chứa 2 dây cung của đường tròn và có đỉnh nằm trên đường tròn. Cung bị chắn là cung nằm trong góc nội tiếp.

Định lý: Trong đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.

Hệ quả:

• Góc nội tiếp bằng nhau thì chắn các cung bằng nhau
• Các góc nội tiếp đường tròn cùng chắn 1 cung hay chắn các cung bằng nhau thì có số đo bằng nhau.
• Góc nội tiếp (nhỏ hơn hoặc bằng 90 độ) có số đo bằng 1 nửa số đo của góc ở tâm tương ứng cùng chắn 1 cung.
• Góc nội tiếp chắn nửa đường tròn là góc vuông.

Các dạng toán liên quan đến góc nội tiếp chắn nửa đường tròn

Dạng 1 - Chứng minh tam giác đồng dạng, 2 góc bằng nhau, các hệ thức về cạnh

Phương pháp giải: Dùng hệ quả đã nêu để chứng minh

Bài 1

Cho đường tròn tâm O và 2 dây cung song song AB, CB. Trên cung AB lấy điểm M, hãy chứng minh rằng AMC = BMD .

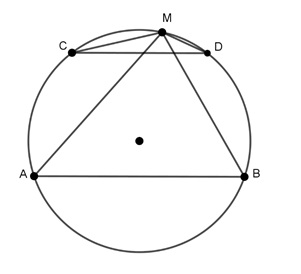
Cách giải:

Ta có: AMC là góc nội tiếp chắn cung AC

BMD là góc nội tiếp chắn cung DB

Ta lại có AB // CD nên cung AC = cung BD

Vì vậy AMC = BMD (2 góc nội tiếp chắn 2 cung bằng nhau).

Bài 2

Cho tam giác nhọn ABC nội tiếp đường tròn tâm O, biết góc BAC = 45 độ. Hãy tính số đo góc CBA.

Cách giải:

Ta có: CDB = CAB = ½ sđ CB => CDB = 45 độ

Cùng với đó: DCB = 90 độ (góc nội tiếp chắn nửa đường tròn)

=> CBD = 180 độ - CDB - DCB = 180 độ - 45 độ - 90 độ = 45 độ

Kết luận CBD = 45 độ.

Bài 3

Cho đường tròn tâm O với đường kính BC cố định. Điểm A di động trên đường tròn không trùng B và C. Hãy vẽ đường kính AD và xác định vị trí A để tam giác ABC có diện tích lớn nhất. Và lúc này góc ADC bằng bao nhiêu?

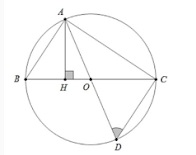
Cách giải:

Vẽ đường cao AH của ABC

AHO vuông tại H nên AH <= AO (dấu bằng xảy ra khi H trùng với O)

S(ABC) = ½ AH.BC <= ½ AO.BC = ½ R.2R = R^2 (dấu bằng xảy ra khi H trùng với O)

Vậy diện tích tam giác ABC đạt giá trị lớn nhất khi H trùng O.

Khi đó A là điểm chính giữa BC => ADC = 45 độ.

Dạng 2 - Chứng minh 2 đường thẳng vuông góc hoặc song song

Phương pháp giải: Chúng ta sử dụng hệ quả để suy ra các góc bằng nhau. Từ đó chứng minh theo yêu cầu của bài toán.

Bài 1

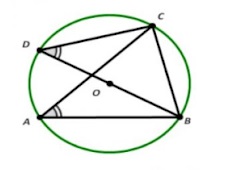
Cho đường tròn tâm O đường kính AB, 2 điểm E và F nằm trên một đường tròn. Các đường thẳng AE, BF cắt nhau tại điểm P nằm ngoài đường tròn. AF và BE cắt nhau tại Q. Hãy chứng minh rằng PQ vuông góc với AB.

Cách giải:

Ta có: AEB và AFB là góc nội tiếp chắn nửa đường tròn nên AEB = AFB = 90 độ.

=> AF vuông góc PB, BE vuông góc PA

Xét PAB ta có: AF vuông góc PB và BE vuông góc PA

Mà AF BE = {Q}

=> Q là trực tâm của PAB

Từ đó kết luận PQ vuông góc với AB.

Bài 2

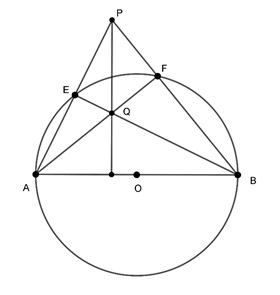
Cho đường tròn tâm O, bán kính R và điểm M bên trong đường tròn đó. Qua M kẻ 2 dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE, hãy chứng minh rằng:

1. MA.MB = MC.MD
2. Tứ giác ABEC là hình thang cân
3. Tổng MA^2 + MB^2 + MC^2 + MD^2 có giá trị không thay đổi khi M đổi vị trí trong đường tròn.

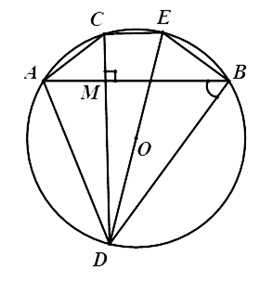
Cách giải:

1. Xét AMC và DMB ta có:

ACD = ABD (hai góc nội tiếp cùng chắn cung AD)

AMC = BMD = 90 độ

=> AMC ∼ DMB

=> MA/MD = MC/MB ⇔ MA.MB = MC.MD

2. Ta có: DCE = 90 độ (góc nội tiếp chắn nửa đường tròn)

=> CD vuông góc CE mà CD vuông góc AB

=> AB // CE

=> Tứ giác ABEC là hình thang (1)

Mặt khác: CE và AB là 2 dây song song của đường tròn tâm O chắn 2 cung AC và BE nên cung AC = cung BE.

Ta lại có: cung AE = cung AC + cung CE

Cung BC = cung BE + cung CE

=> cung AE = cung BC => ABE = BAC (hai góc nội tiếp chắn 2 cung bằng nhau (2)

Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân.

3. Vì cung AE = cung BC (chứng minh ở trên) => AE = BC

Mặt khác DAE = 90 độ (góc nội tiếp chắn nửa đường tròn)

Xét vuông tại A ta có: AD^2 + AE^2 = DE^2 (định lý Py-ta-go)

Xét tổng MA^2 + MB^2 + MC^2 + MD^2 = (MA^2 + MD^2) + (MB^2 + MC^2)

= AD^2 + BC^2 = AD^2 + AE^2 = DE^2 = 4R^2 không đổi.

Tổng kết

Bài viết trên đây vừa tổng hợp các kiến thức về lý thuyết và các dạng bài tập liên quan đến góc nội tiếp chắn nửa đường tròn kèm lời giải chi tiết nhất. Hy vọng có thể hỗ trợ các em học tập hiệu quả và đạt điểm cao trong các bài thi sắp tới. Nhớ theo kênh thường xuyên để cập nhật thêm nhiều bài học mới nhất và hữu ích nhất nhé!