Lý thuyết về các phép toán giao hợp hiệu & bài tập đặc trưng

Tổng hợp đầy đủ lý thuyết về các phép toán giao hợp hiệu. Các dạng bài tập liên quan kèm lời giải chi tiết, dễ hiểu nhất.

Các phép toán tập hợp giao hợp hiệu là một phần kiến thức trong chương trình Toán lớp 10. Để làm tốt bài tập dạng này các em cần nắm chắc lý thuyết và luyện tập thường xuyên. Cùng thayphu tham khảo ngay bài viết sau đây để cập nhật các nội dung hữu ích nhé!

Lý thuyết các phép toán tập hợp: Giao hợp hiệu

Phép hợp

Hợp của 2 tập hợp A và B là tập hợp bao gồm tất cả các phần tử thuộc A hoặc thuộc B và được ký hiệu là A U B.

A ∩ B ⇔ {x| x thuộc A và x thuộc B}

Ví dụ ta cho tập hợp A = {2;3;4} và B = {1;2}. Vậy A U B = {1;2;3;4}

Phép hợp hợp bao gồm các phần tử thuộc A hoặc thuộc B

Phép giao

Giao của 2 tập hợp A, B là tập hợp bao gồm tất cả các phần tử thuộc cả A và B. Được ký hiệu là A ∩ B. A U B ⇔ {x|x thuộc A hoặc x thuộc B}

Nếu cả 2 tập hợp A và B không có phần tử chung thì A ∩ B = rỗng. Khi đó ta nói A và B là 2 tập hợp rời nhau.

Ví dụ ta có tập A = {2;3;4} và B = {1;2}. Vậy A ∩ B = {2}

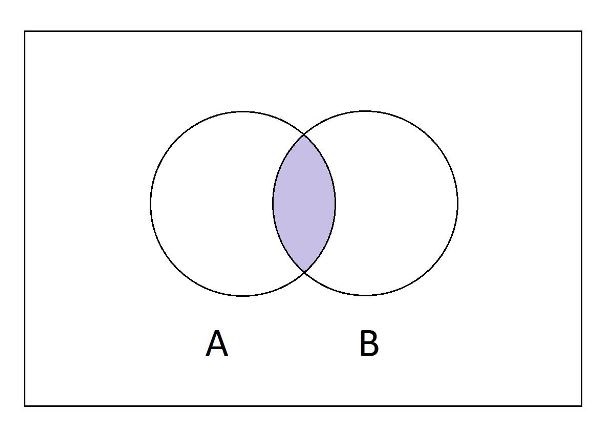
Phép giao bao gồm các phần tử thuộc A và B

Phép hiệu

Hiệu của tập hợp A và B là tập hợp tất cả các phần tử thuộc A nhưng lại không thuộc B và được ký hiệu là A\B.

A\B = x|x thuộc A và x không thuộc B.

Ví dụ ta cho tập hợp A = {2;3;4} và B = {1;2} thì:

A\B = {3;4}

B\A = {1}

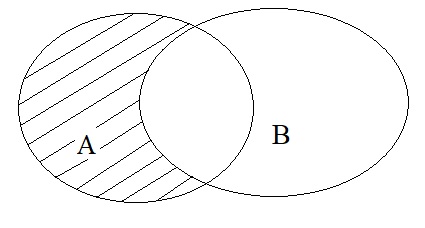
Phép hiệu tập hợp tất cả các phần tử thuộc A nhưng lại không thuộc B

Một số bài tập về các phép toán giao hợp hiệu

Bài 1

Cho A là tập hợp học sinh lớp 10 đang học ở trường. B là tập hợp các học sinh đang học tiếng Anh của trường. Hãy diễn đạt các tập hợp A U B; A ∩ B; A\B và B\A.

Giải:

• A U B: Tập hợp các học sinh hoặc học sinh lớp 10 hoặc học sinh học môn tiếng Anh của trường.
• A ∩ B: Tập hợp học sinh lớp 10 học môn tiếng Anh của trường.
• A\B: Tập hợp các học sinh học lớp 10 nhưng không học môn tiếng Anh của trường.
• B\A: Tập hợp các học sinh học môn tiếng Anh của trường em nhưng không học lớp 10 của trường.

Bài 2

Cho 3 tập là A = {1;2;3;4;5;6;9}, B = {1;2;4;6;8;9} và C = {3;4;5;6;7}

1. Hãy tìm 2 tập hợp (A\B) U (B\A) và (A U B) \\ (A ∩ B). Vậy 2 tập hợp nhận được có bằng nhau không?
2. Tìm A ∩ (B\C) và (A ∩ B) \ C. Vậy 2 tập hợp nhận được có bằng nhau không?

Giải:

1. Ta có A\B = {3;5} và B\A = {8}

=> (A\B) U (B\A) = {3;5;8}

A U B = {1;2;3;4;5;6;8;9}

A ∩ B = {1;2;4;6;9}

=> (A U B) \\ (A ∩ B) = {3;5;8}

Từ đó kết luận: (A\B) U (B\A) = (A U B) \\ (A ∩ B)

2. B\C = {1;2;8;9}

=> A ∩ (B\C) = {1;2;9}

A ∩ B = {1;2;4;6;9}

=> (A ∩ B) \ C = {1;2;9}

Từ đó kết luận A ∩ (B\C) = (A ∩ B) \ C.

Bài 3

Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó:

1. A = {2;3;5;7}
2. B = {-3;-2;-1;0;1;2;3}
3. C = {-5;0;5;10;15}

Giải:

1. A là tập hợp các số nguyên tố nhỏ hơn 10
2. B là tập hợp các số nguyên có giá trị tuyệt đối không vượt quá 3

B = {x thuộc Z ||x| <= 3}

3. C là tập hợp các số nguyên n chia hết cho 5 sao cho không nhỏ hơn - 5 và không lớn hơn 15.

C = {n thuộc Z|-5 <= n <= 15; n chia hết cho 5}

Tổng hợp các câu hỏi trắc nghiệm về các phép giao hợp hiệu kèm đáp án

Câu 1

Đề cho các tập hợp A = {M thuộc N| m là ước của 16}; B = {n thuộc N| n là ước của 24}

Vậy tập hợp A ∩ B sẽ là:

1. A ∩ B = rỗng
2. A ∩ B = {1;2;4;8}
3. A ∩ B = {+-1; +-2; +-4; +-8}
4. A ∩ B = {1;2;4;8;16}

Giải:

Ta có: A = {M thuộc N | m là ước của 16} = {1;2;4;8;16}

B = {N thuộc N | n là ước của 24} = {1;2;3;4;6;8;12;24}

=> A ∩ B = {1;2;4;8}

Lưu ý A ∩ B chính là tập hợp các ước số tự nhiên của 8 = Ước chung lớn nhất (16;24).

Như vậy A ∩ B = {1;2;4;8} => chọn đáp án B.

Câu 2

Xác định tập hợp X sao cho thỏa mãn 2 điều kiện X U {1;2;3} = {1;2;3;4} và X ∩ {1;2;3;a} = {2;3}

1. X = {2;3}
2. X = {1;2;3;4}
3. X = {2;3;4}
4. X = {2;3;4;a}

Giải:

Vì X U {1;2;3} = {1;2;3;4} nên 4 thuộc X và tập X {1;2;3;4}

Vì X ∩ {1;2;3;a} = {2;3} nên 2;3 thuộc X và 1 không thuộc X, a không thuộc X.

Do đó X = {2;3;4} => chọn đáp án C.

Câu 3

Cho A = {a,b,c,d,e} và B = {c,d,e,k} thì tập hợp A ∩ B sẽ là:

1. A ∩ B = {a,b}
2. A ∩ B = {c,d,e}
3. A ∩ B = {a,b,c,d,e,k}
4. A ∩ B = {a,b;k}

Giải:

Ta có A = {a,b,c,d,e} và B = {c,d,e,k}

Tập hợp A ∩ B = {c,d,e} => chọn đáp án B.

Vừa rồi là tổng hợp phần lý thuyết và các bài tập kèm lời giải cho phép toán giao hợp hiệu. Hy vọng các em đã có những phút giây học tập hữu ích và hoàn thành tốt mọi đề thi. Đừng quên theo dõi kênh thường xuyên để cập nhật nhiều bài học hay nhé!