Đường trung trực của tam giác, định nghĩa và bài tập

Trong 1 tam giác, đường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó. Tính chất và các dạng bài tập liên quan đến đường trung trực.

Đường trung trực của tam giác là một nội dung quan trọng trong chương trình Toán lớp 7. Hãy cùng thayphu ôn tập lại các khái niệm, tính chất và bài tập liên quan đến đường trung trực qua bài viết sau đây!

Lý thuyết đường trung trực của tam giác

Đường trung trực của tam giác là gì?

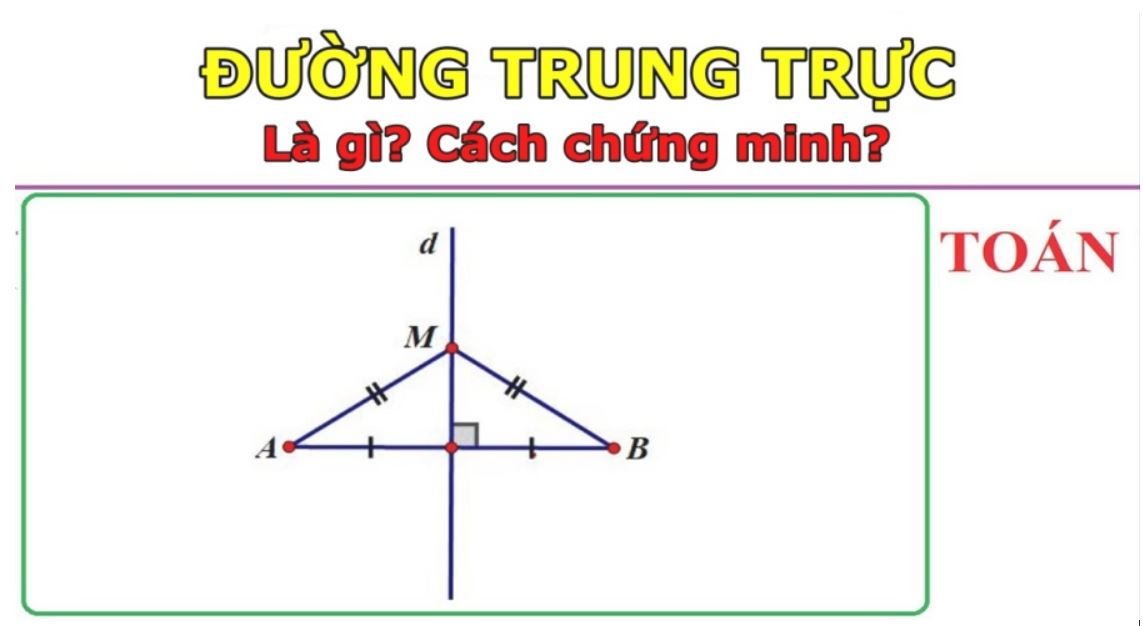
Đường trung trực của tam giác là đường thẳng vuông góc và đi qua trung điểm của mỗi cạnh của tam giác đó.

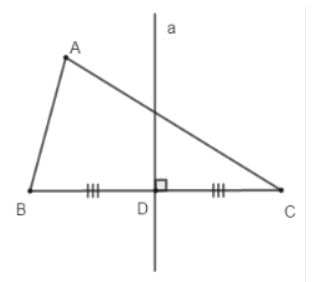
Ví dụ: a là đường trung trực ứng với cạnh BC của tam giác ABC.

• Mỗi tam giác có 3 đường trung trực.

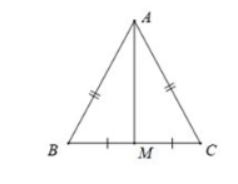
Tính chất: Trong 1 tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.

Ta có: Tam giác ABC cân tại A có đường trung trực của đoạn thẳng BC là AM. Khi đó AM cũng là trung tuyến ứng với cạnh BC của tam giác ABC.

Tính chất ba đường trung trực của tam giác

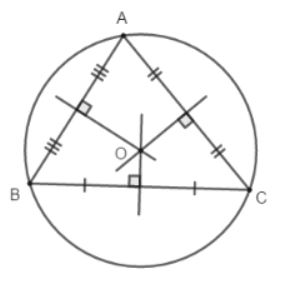
Ba đường trung trực của 1 tam giác cùng đi qua 1 điểm. Điểm này cách đều 3 đỉnh của tam giác đó.

Điểm O là giao điểm 3 đường trung trực của tam giác ABC. Ta có: OA = OB = OC.

Lưu ý:

Vì giao điểm O của 3 đường trung trực của tam giác ABC cách đều 3 đỉnh của tam giác đó nên có 1 đường tròn tâm O đi qua 3 đỉnh A, B, C. Đường tròn đó được gọi là đường tròn ngoại tiếp tam giác ABC.

Các dạng bài tập về đường trung trực của tam giác

Trong Toán học lớp 7, có tổng cộng 4 dạng bài tập về đường trung trực của một tam giác, để biết cụ thể hãy cùng xem ngay bên dưới:

Dạng 1 - Vận dụng tính chất của đường trung trực

Phương pháp giải:

Sử dụng định lí 1: Điểm nằm trên đường trung trực của 1 đoạn thẳng thì cách đều 2 mút của đoạn thẳng đó.

Bài tập vận dụng:

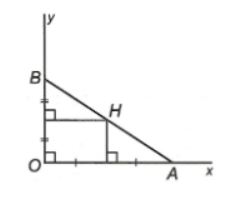
Cho góc vuông xOy, trên các tia Ox, Oy lần lượt lấy 2 điểm A, B (không trùng với O). Đường trung trực của các đoạn thẳng OA và OB cắt nhau tại H.

1. Chứng minh rằng các điểm A, H, B thẳng hàng

2. Chứng minh H là trung điểm của AB

Cách giải:

1. Ta có H thuộc trung trực của OA, OB

=> HA = HO = HB

=> AHO, BHO cân tại H

=> AHO = 180 độ - 2AOH (tổng 3 góc trong tam giác)

BHO = 180 độ - 2BOH

=> AHB = AHO + BHO = 180 độ - 2AOH + 180 độ - 2BOH

= 360 độ - 2(AOH + BOH)

= 360 độ - 2AOB = 360 độ - 2.90 độ = 180 độ

Như vậy A, H, B thẳng hàng.

2. Từ kết quả của a) ta có: HA = HB và 3 điểm A, H, B thẳng hàng nên H là trung điểm của AB.

Dạng 2 - Chứng minh 1 điểm thuộc đường trung trực, 1 đường thẳng là đường trung trực của 1 đoạn thẳng

Phương pháp giải:

• Sử dụng định lí 2: Điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. Hoặc dùng định nghĩa đường trung trực.

• Để chứng minh đường thẳng d là đường trung trực của đoạn thẳng AB, ta chứng minh d chứa 2 điểm cách đều A và B, hoặc dùng định nghĩa đường trung trực.

Bài tập vận dụng:

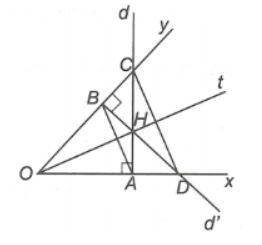
Cho góc xOy (0 < xOy < 90 độ), Ot là tia phân giác của xOy và H là 1 điểm bất kỳ thuộc tia Ot. Qua H lần lượt vẽ đường thẳng d và d’ thỏa mãn d vuông góc với Ox tại A, cắt Oy tại C. d’ vuông góc với Oy tại B, cắt Ox tại D. Hãy chứng minh:

1. OH là đường trung trực của AB

2. Điểm H thuộc đường trung trực của CD

Cách giải:

1. Xét HAO và HBO có:

HAO = HBO = 90 độ (vì HA Ox, HB Oy)

HOA = HOB (do OH là phân giác của xOy

OH là cạnh chung

Do đó: HAO = HBO (cạnh huyền - góc nhọn)

=> OA = OB và HA = HB (các cạnh tương ứng)

=> OH là trung trực của AB (tính chất đường trung trực của 1 đoạn thẳng)

2. Xét 2 OAC và OBD có:

OAC = OBD = 90 độ (HA Ox, HB Oy)

OA = OB (chứng minh trên)

Góc O chung

Do đó OAC = OBD (g.c.g) => OD = OC (2 cạnh tương ứng)

• Xét 2 ODH và OCH có:

OD = OC (chứng minh trên)

HOD = HOC (do OH là phân giác xOy

OH là cạnh chung

Do đó ODH = OCH (g.c.g) => HD = HC (2 cạnh tương ứng)

=> H thuộc đường trung trực của CD (tính chất đường trung trực của 1 đoạn thẳng)

Dạng 3 - Xác định vị trí của điểm thỏa mãn yêu cầu đề bài

Phương pháp giải:

Sử dụng định lí 2: Điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó. Từ đó chúng ta xác định 1 điểm nằm trên đường trung trực của đoạn thẳng.

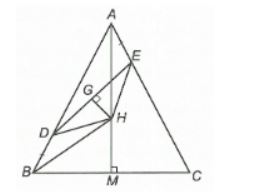
Bài tập vận dụng: Cho ABC cân tại A, trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho BD = AE. Chứng minh đường trung trực của DE luôn đi qua 1 điểm cố định.

Cách giải:

Gọi H là giao điểm của 3 đường trung trực của ABC

=> HA = HB (tính chất đường trung trực của 1 đoạn thẳng)

ABH cân tại H (định nghĩa tam giác cân)

=> HBA = HAB (tính chất tam giác cân) (1)

Vì ABC cân tại A nên đường trung trực AH đồng thời là đường phân giác của góc A.

=> HAB = HAC (2)

Từ (1) (2) ta có: HBA = HAC hay HBD = HAE

Xét 2 HBD và HAE ta có:

• HA = HB (chứng minh trên)

• HBD = HAE (chứng minh trên)

• BD = AE (giả thiết)

Do đó: HBD = HAE (c.g.c) => HD = HE (2 cạnh tương ứng)

=> H thuộc trung trực của DE (tính chất đường trung trực của 1 đoạn thẳng)

Mà H cố định nên đường trung trực của DE luôn đi qua 1 điểm cố định.

Dạng 4 - Sử dụng tính chất đường trung trực vào bài toán về cực trị

Phương pháp giải:

• Sử dụng tính chất đường trung trực để thay đổi độ dài một đoạn thẳng bằng độ dài một đoạn thẳng khác bằng nó.

• Sử dụng bất đẳng thức tam giác để tìm giá trị nhỏ nhất, giá trị lớn nhất.

Bài tập vận dụng:

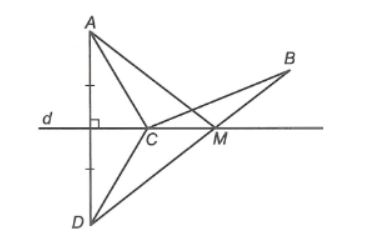
Hai điểm A và B cùng nằm trên nửa mặt phẳng có bờ là đường thẳng d. Tìm vị trí của điểm C trên đường thẳng d sao cho giá trị của tổng CA + CB là nhỏ nhất.

Cách giải:

Bước 1: Xây dựng cặp tổng độ dài đoạn thẳng trung gian

Lấy điểm D đối xứng với A qua d. Theo tính chất đường trung trực ta có: CA = CD.

Do đó: CA + CB = CD + CB

Bước 2: Lập luận để xác định vị trí điểm cần tìm

Gọi M là giao điểm của BD và d.

Nếu C không trùng với M thì xét BCD ta có:

CB + CD > BD hay CA + CB > BD (1)

Nếu C trùng với M thì:

CA + CB = MA + MB = MD + MB = BD (2)

Từ (1) (2) => CA + CB >= BD

Do đó khi C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB nhỏ nhất.

Bài tập tự luyện

Bài tập 1:

Cho tam giác ABC cân tại A. Hai đường trung tuyến BM, CN cắt nhau tại I. Hai tia phân giác trong của góc B và C cắt nhau tại O. Hai đường trung trực của 2 cạnh AB và AC cắt nhau tại K.

1. Chứng minh rằng BM = CN

2. Chứng minh rằng OB = OC

3. Chứng minh các điểm A, O, K thẳng hàng

Bài tập 2: Trên đường thẳng d là trung trực của đoạn thẳng AB lấy điểm M, N nằm ở 2 nửa mặt phẳng đối nhau có bờ là đường thẳng AB.

1. Chứng minh MAN = MBN

2. Chứng minh MN là tia phân giác của AMB

Bài tập 3: Cho 2 điểm A và B nằm trên cùng 1 nửa mặt phẳng có bờ là đường thẳng d. Vẽ điểm C sao cho d là trung trực của đoạn thẳng BC, AC cắt d tại E. Trên d lấy điểm M bất kỳ.

1. So sánh MA + MB và AC

2. Tìm vị trí của M trên d để MA, MB ngắn nhất

Qua bài viết trên, thayphu.net đã chia sẻ nội dung kiến thức về đường trung trực của tam giác và các dạng bài tập liên quan. Các em nắm vững phương pháp giải để áp dụng thực hành hiệu quả nhé!