Đường elip Toán lớp 10, tổng hợp kiến thức và các dạng bài tập

Cùng tìm hiểu về đường elip Toán lớp 10 với đầy đủ các phần lý thuyết, công thức, phương pháp giải và bài tập dụng chi tiết.

Đường elip Toán lớp 10 là một trong những nội dung quan trọng. Để hoàn thành tốt các dạng bài này các em phải nắm vững phần lý thuyết, công thức, phương phương giải. Và đặc biệt là thực hành làm nhiều bài tập. Hãy cùng theo ngay bài viết sau đây của thayphu để bổ sung các kiến thức hữu ích nhé!

Lý thuyết về đường elip trong Toán lớp 10

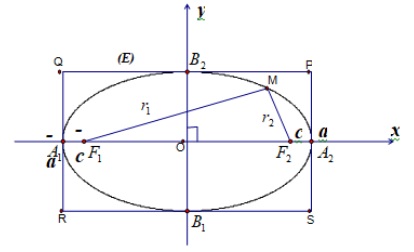
Trong mặt phẳng, cho 2 điểm cố định F1, F2 và tập hợp các điểm M sao cho tổng F1M + F2M = 2a không đổi được gọi là elip. Các điểm F1, F2 được gọi là tiêu điểm của elip. Khoảng cách F1F2 = 2c được gọi là tiêu cự của elip.

Phương trình chính tắc của elip

Ta cho elip có tiêu điểm F1, F2 chọn hệ trục tọa độ Oxy với F1(-c;0) và F2(c;0). Khi đó chứng minh được M (x;y) thuộc elip => x^2 / a^2 + y^2 / b^2 = 1 (1)

Trong đó: b^2 = a^2 - c^2

Như vậy phương trình (1) được gọi là phương trình chính tắc của đường elip.

Ví dụ:

Trong mặt phẳng hệ trục tọa độ Oxy, cho elip có độ dài trục lớn là 12, độ dài trục bé là 6. Yêu cầu viết phương trình chính tắc của elip?

Cách giải:

Theo công thức, phương trình chính tắc của elip sẽ có dạng là x^2 / a^2 + y^2 / b^2 = 1 với a,b > 0.

Ta có độ dài trục lớn là 12 => 2a = 12 => a = 6

Tương tự độ dài trục bé là 6 => 2a = 6 => b = 3

Kết luận phương trình chính tắc của elip là x^2 / 6^2 + y^2 / 3^2 = 1

Thành phần và hình dạng của elip

Với elip có phương trình chính tắc x^2 / a^2 + y^2 / b^2 = 1

Nếu điểm M(x;y) thuộc elip thì các điểm M1 (-x;y), M2(x;-y) cũng thuộc elip.

Như vậy elip sẽ có các trục đối xứng là Ox, Oy và tâm đối xứng là gốc O.

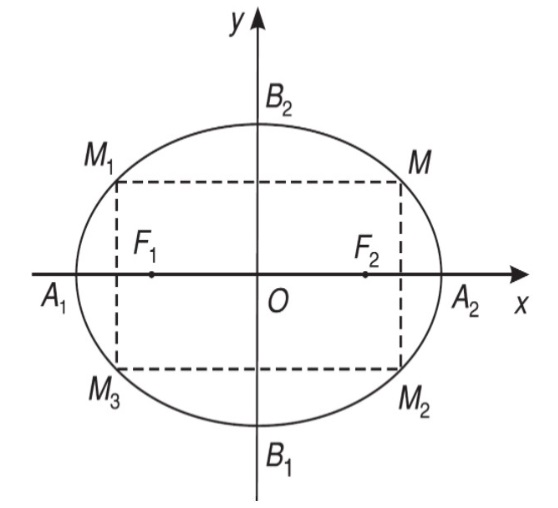
Thay y = 0 vào x^2 / a^2 + y^2 / b^2 = 1 ta có x = +- a

Như vậy đường elip cắt Ox tại 2 điểm là A1(-a;0) và A2(a;0).

Tương tự thay x = 0 vào x^2 / a^2 + y^2 / b^2 = 1 ta được y = b.

Như vậy đường elip cắt Oy tại 2 điểm B1(0;-a), B2(a;0).

Các điểm A1, A2, B1, B2 được gọi là các đỉnh của elip. Đoạn thẳng A1, A2 là trục lớn, đoạn thẳng B1, B2 là trục nhỏ của elip.

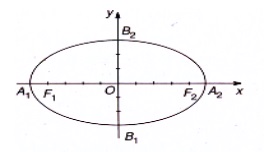
Ví dụ: Hãy xác định độ dài các trục, tọa độ các tiêu điểm, tọa độ các đỉnh và vẽ elip có phương trình là x^2/25 + y^2/9 = 1.

Ta có phương trình elip có dạng là x^2 / a^2 + y^2 / b^2 = 1

Theo đề bài ta được: a^2 = 25 và b^2 = 9 ⇔ a = 5 và b = 3

c = a2 - b2 = 4

Như vậy elip sẽ có trục lớn là A1A2 = 2a = 10

• Trục nhỏ là B1B2 = 2b = 6
• Hai tiêu điểm là F1(-4;0), F2(4;0)
• Bốn đỉnh là A1(-5;0), A2(5;0), B1(0;-3), B2(0;3).

Các dạng bài tập về đường elip Toán lớp 10

Bài tập 1

Cho phương trình elip (E) là x^2/16 + y^2/12 = 1 cùng điểm M nằm trên (E). Giả sử điểm M có hoành độ = 1 thì khoảng cách từ M đến 2 tiêu điểm của (E) bằng bao nhiêu?

Giải:

Ta có a^2 = 16 và b^2 = 12 nên c^2 = a^2 - b^2 = 4 => a = 4, c = 2.

Hai tiêu điểm có tọa độ là F1(-2;0) và F2(2;0).

Điểm M thuộc (E), xM = 1 => yM = +- 35/2

Tâm sai của elip là e = c/a => e = 2/4 = ½

=> MF1 = a + exM = 4 + 0.5 = 4.5

MF2 = a - exM = 4 - 0.5 = 3.5

Bài tập 2

Cho mặt phẳng tọa độ Oxy, hãy viết phương trình chính tắc của elip (E) biết tâm sai là 3/3, độ dài đường chéo hình chữ nhật cơ sở là 25.

Giải:

Ta có phương trình chính tắc của elip có dạng là x^2/a^2 + y^2/b^2 với a > b > 0.

Tâm sai là e = c/a = 3/3 ⇔ c^2 = a^2 / 3.

Độ dài của đường chéo hình chữ nhật là (2a)2 + (2b)2 = 25

⇔ a^2 + b^2 = 5 ⇔ b^2 = 5 - a^2

Như vậy a^2 = b^2 + c^2 ⇔ a^2 = 5 - a^2 + a^2 / 3 ⇔ a^2 = 3 => b^2 = 2

Kết luận phương trình chính tắc của elip cần lập là x^2 / 3 + y^2 / 2 = 1.

Bài tập 3

Trong mặt phẳng tọa độ Oxy, hãy viết phương trình chính tắc của elip (E). Cho 2 tiêu điểm F1, F2 với F1(-3; 0) và một điểm M thuộc elip để tam giác F1MF2 vuông tại M, có S = 1.

Giải:

Ta có phương trình chính tắc của (E) là x^2/a^2 + y^2/b^2 (1) a > b > 0.

Với F1(-3; 0) thì ta được c = 3 => a^2 - b^2 - c^2 = 3 hay a^2 = b^2 + 3 (1)

Gọi điểm M có tọa độ (x0; y0)

=> MF1 = (-3 - x0; -y0) và MF2 = (3 - x0; -y0)

Lúc này góc F1MF2 = 90 độ ⇔ MF1. MF2 = 0

⇔ x0^2 - 3 + y0^2 = 0 ⇔ x0^2 + y0^2 = 3.

Ta có diện tích S(F1MF2) = ½ d(M,Ox).F1F2 = ½ |y0|.23 = 3 |y0| = 1

⇔ y0^2 = ⅓ => x0^2 = 8/3.

Bên cạnh đó M(x0;y0) thuộc elip

⇔ x0^2 / a^2 + y0^2 / b^2 = 1 ⇔ 8/3a^2 + 1/3b^2 = 1 (2)

Thực hiện thay (1) vào (2) ta có:

8/ 3(b^2 + 3) + 1/3b^2 = 1 ⇔ 3b^4 = 3 ⇔ 1 => a^2 = 4.

Kết luận phương trình chính tắc của elip cần tìm chính là x^2 / 4 + y^2 = 1.

Trên đây là tổng hợp các kiến thức và bài tập liên quan đến đường elip Toán lớp 10. Chúc các em học thật tốt và hoàn thành các bài thi chính xác nhất nhé!