Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc 4

Tổng hợp kiến thức liên quan đến đồ thị hàm số bậc 4, cách khảo sát sự biến thiên, vẽ đồ thị hàm số bậc 4 và bài tập áp dụng.

Xác định đồ thị hàm số bậc 4 là dạng bài gây không ít khó khăn cho các em khi giải. Tuy nhiên chỉ cần nắm phương pháp giải cùng 1 số mẹo nhỏ thì sẽ thấy đơn giản và dễ hiểu hơn.

Hãy cùng thayphu.net tham khảo ngay các nội dung, đặc điểm, phương pháp khảo sát hàm số bậc 4. Cùng với đó là bài tập minh họa chi tiết nhất!

Định nghĩa về hàm số bậc 4

Tổng hợp kiến thức liên quan đến hàm số và đồ thị hàm số bậc 4

Hàm số bậc 4 là phương trình có dạng y = ax^4 + bx^3 + cx^2 + dx + e với a khác 0 và a, b, c, d, e là các hệ số thực. Đồ thị của hàm số bậc 4 có tối đa 4 điểm uốn. Điểm uốn chính là điểm mà độ cong của đồ thị thay đổi từ uốn lên uốn xuống hay ngược lại.

Để xác định đồ thị hàm số ta thực hiện theo các bước:

• Đầu tiên xác định điểm uốn: Bằng cách tính đạo hàm bậc 2 (đạo hàm của hàm số) và giải phương trình f\’\’(x) = 0.
• Xác định điểm cực trị (điểm trong đồ thị mà giá trị hàm số đạt cực đại hoặc cực tiểu): Bằng cách giải phương trình f\’(x) = 0.
• Xác định điểm cắt trục hoành: Bằng cách giải phương trình f(x) = 0.
• Cuối cùng xác định đường viền bằng cách phân tích dấu của đạo hàm bậc 2.

Sau khi tìm được các điểm trên, ta tiến hành vẽ đồ thị, biểu diễn sự biến thiên và các giá trị cực trị, điểm uốn, điểm cắt trục hoành.

Đặc điểm của đồ thị hàm số bậc 4

• Tính đơn điệu: Có thể tăng hoặc giảm trên toàn miền xác định
• Điểm uốn: Đồ thị có thể có tối đa 3 điểm uốn
• Điểm cực trị: Tùy thuộc vào dạng hàm số mà có tối đa 3 điểm cực tiểu hoặc điểm cực đại.
• Đồ thị có thể bị chặn hoặc không bị chặn tùy vào dạng của hàm số.
• Với các nghiệm của phương trình bậc 4, hàm số có thể có tối đa 4 điểm cắt trục Ox.
• Đồ thị của hàm số có thể đối xứng hoặc không đối xứng qua trục đối xứng.

Ta có thể sử dụng các kiến thức thức về đạo hàm và nghiệm của phương trình bậc 4 như sau:

• Hàm số có 1 cực trị ⇔ ab >= 0
• Hàm số có 3 cực trị ⇔ ab < 0
• Hàm số có duy nhất 1 cực trị và cực trị là cực tiểu ⇔ a > 0 và b >= 0
• Hàm số có duy nhất 1 cực trị và cực trị là cực đại ⇔ a < 0 và b <= 0
• Hàm số có 2 cực tiểu và 1 cực đại ⇔ a > 0 và b < 0
• Hàm số có 1 cực tiểu và 2 cực đại ⇔ a < 0 và b > 0.

Sơ đồ khảo sát và vẽ đồ thị hàm số bậc 4

Cho hàm số bậc 4 có dạng là y = ax^4 + bx^2 + c (với a khác 0). Tập xác định D = R.

Đầu tiên xét chiều biến thiên của hàm số:

• Tính đạo hàm y’ = 4ax^3 + 2bx

y’ = 0 ⇔ 4a^3 + 2bx = 0 ⇔ 2x(2ax^2 + b) = 0

⇔ x = 0 ⇔ x = 0 và 2a^2 + b = 0 ⇔ x^2 = -b/2a

Xét dấu đạo hàm y ’và suy ra chiều biến thiên của hàm số.

Tiếp đó tìm cực trị và tìm các điểm giới hạn tại vô cực (x đến âm vô cực hoặc dương vô cực). Lập bảng biến thiên thể hiện đầy đủ và chính xác các giá trị bao gồm x, y’,y).

Vẽ đồ thị hàm số bậc 4

• Giao của đồ thị với trục Oy có x = 0 => y = c => (0;c)
• Giao của đồ thị với trục Ox có y = 0 ⇔ ax^4 + bx^2 + c = 0 ⇔ x = ? => (?;0)
• Tìm các điểm cực đại, cực tiểu nếu có.

Lưu ý: Giải phương trình bậc 4 các em sử dụng máy tính như giải phương trình bậc 2 nhưng chỉ lấy nghiệm không âm để tìm x.

• Nhận xét về đặc trưng của đồ thị ta có y(-x) = a(-x)^4 + b(-x)^2 + c = ax^4 + bx^2 + c = y(x). Như vậy đồ thị hàm số trên là hàm số chẵn nên nhận trục Oy làm trục đối xứng.

Các dạng đồ thị hàm số bậc 4: y = ax^4 + bx^2 + c (với a khác 0)

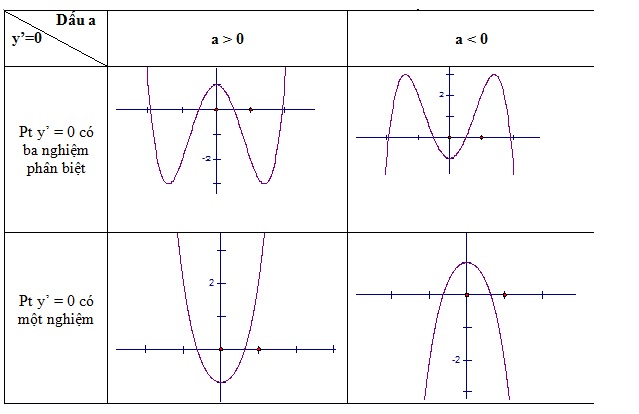
Các dạng đồ thị của hàm số bậc 4

Bài tập ứng dụng

Cho hàm số y = x^4 - 2x^2 - 3, yêu cầu khảo sát sự biến thiên và vẽ đồ thị của hàm số.

Hàm số y = x^4 - 2x^2 - 3 có tập xác định là R.

Giới hạn của hàm số tại vô cực là lim y (x->âm vô cực) = dương vô cực và lim y (x ->dương vô cực) = dương vô cực.

Ta có: y’ = 4x(x^2 - 1)

y’ = 0 ⇔ x = 0, x = 1, x = -1

Tiến hành lập bảng biến thiên như sau:

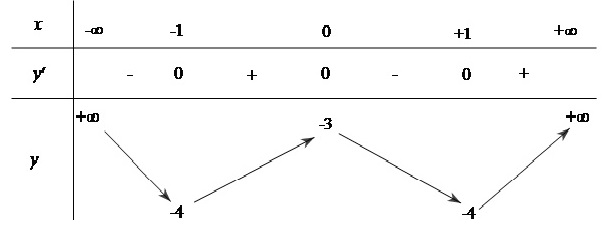
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên mỗi khoảng (âm vô cùng; -1) & (0; 1) và đồng biến trên mỗi khoảng (-1; 0) & (1; dương vô cùng).

Hàm số đạt cực đại tại điểm x = 0, giá trị cực đại tại y (0) = -3.

Hàm số đạt cực tiểu tại điểm x = 1 và x = -1, hàm số đạt giá trị cực tiểu tại điểm y(+-1) = -4.

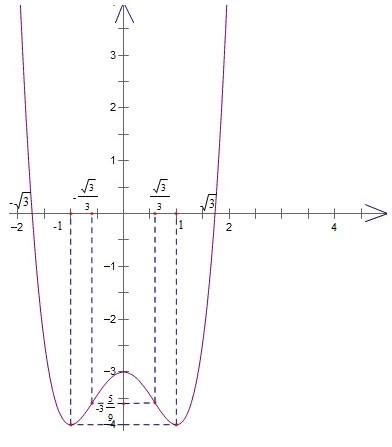
Với y” = 12x^2 - 4

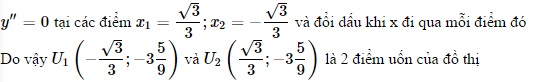
Đồ thị của hàm số giao với trục tung tại điểm (0;-3)

Lưu ý

Gọi C là đồ thị hàm số y = ax^4 + bx^2 + c (với a khác 0).

• Nếu phương trình f”(x) = 0 có 2 nghiệm phân biệt x = +- x0 (x0 > 0) thì C có 2 điểm uốn U1 (x0; f(x0)) và U2(-x0; f(-x0)) x0 đối xứng với nhau qua 2 trục tung.
• Nếu phương trình có 1 nghiệm kép hoặc vô nghiệm thì C không có điểm uốn.

Vừa rồi là các kiến thức cùng hướng dẫn khảo sát, vẽ đồ thị hàm số bậc 4 và bài tập ứng dụng. Chúc các em có những giờ phút học tập bổ ích và hoàn thành tốt các đề bài nhé!