Cách vẽ đồ thị hàm số bậc 2 và các dạng bài tập áp dụng

Tổng hợp lý thuyết, cách vẽ đồ thị hàm số bậc 2, các dạng bài tập thường gặp, phương pháp giải và ví dụ chi tiết nhất.

Đồ thị hàm số bậc 2 là phần kiến thức chủ đạo trong chương trình Đại số lớp 10. Các dạng toán từ cơ bản đến nâng cao về hàm số bậc 2 xuất hiện trong rất nhiều kỳ thi quan trọng. Vì vậy bài viết hôm nay của thayphu sẽ tổng hợp đầy đủ các phần lý thuyết, cách vẽ đồ thị, các dạng bài và phương pháp giải chi tiết.

Kiến thức về đồ thị hàm số bậc 2

Hàm số bậc 2 là hàm số có công thức tổng quát dạng y = ax^2 + bx + c. Trong đó a, b, c là các hằng số cho trước và a khác 0. Hàm số sẽ có tập xác định là D = R. Biệt thức Delta (ký hiệu ????) được tính theo công thức ???? = b^2 - 4ac.

Cách vẽ đồ thị hàm số bậc 2 chuẩn nhất

Các cách vẽ đồ thị hàm số bậc 2

Xét chiều biến thiên và bảng biến thiên

Để vẽ được đồ thị hàm số bậc 2 chúng ta phải thực hiện xét chiều biến thiên và bảng biến thiên. Ta cho hàm số y = ax^2 + bx + c với a > 0 thì chiều biến thiên của hàm số sẽ là:

• Đồng biến trên khoảng từ -b/2a cho đến dương vô cùng.
• Nghịch biến trên khoảng từ âm vô cùng đến -b/2a.
• Hàm số đạt giá trị cực tiểu tại (-b/2a; -????/4a). Lúc này giá trị nhỏ nhất của hàm số là -????/4a tại điểm x = -b/2a.

Trường hợp hàm số bậc 2 y = ax^2 + bx + c với a < 0 thì chiều biến thiên sẽ là:

• Đồng biến trên khoảng từ âm vô cùng đến -b/2a.
• Nghịch biến trên khoảng từ -b/2a đến dương vô cùng.
• Hàm số đạt giá trị cực đại tại (-b/2a; -????/4a). Lúc này hàm số có giá trị lớn nhất là -????/4a tại điểm x = -b/2a.

Sau khi xét được chiều biến thiên của hàm số bậc 2 ta tiến hành vẽ được bảng biến thiên như bên dưới:

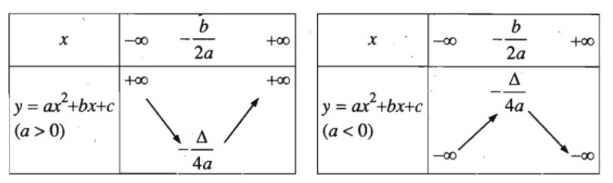
Bảng chiều biến thiên của hàm số bậc 2

Các bước vẽ đồ thị hàm số bậc 2

Đồ thị hàm số y = ax^2 + bx + c (điều kiện a khác 0) là đường parabol có:

• Đỉnh là điểm I (-b/2a; -????/4a)
• Trục đối xứng là đường thẳng x = -b/2a
• Trường hợp a > 0 thì phần lõm của đường parabol sẽ quay lên trên. Ngược lại nếu a < 0 thì phần lõm của đường parabol quay xuống dưới.
• Đồ thị giao với trục tung tại điểm A(0; c)
• Hoành độ giao điểm với trục hoành chính là nghiệm của phương trình dạng ax^2 + bx + c = 0.

Để vẽ đồ thị hàm số bậc hai y = ax^2+ bx + c ta có 2 cách như sau:

Cách 1:

• Đầu tiên xác định tọa độ đỉnh I
• Tiếp đó vẽ trục đối xứng của đồ thị
• Cuối cùng xác định tọa độ các giao điểm của đường parabol với trục tung và trục hoành.

Cách 2:

Cách này sẽ được áp dụng khi đồ thị hàm số có dạng y = ax^2.

• Trường hợp b/2a > 0 tịnh tiến song song với trục hoành |b/2a| đơn vị về bên trái. Hoặc về bên phải trong trường hợp b/2a < 0.
• Xét -????/4a > 0 tịnh tiến song song với trục tung |-????/4a| đơn vị lên trên. Hoặc xuống dưới nếu như -????/4a < 0.

Dạng bài liên quan đến đồ thị hàm số bậc 2 và phương pháp giải

Các dạng bài tập về hàm số bậc 2 khá phổ biến với nhiều cấp độ khác nhau. Sau đây là chi tiết các dạng bài và cách giải kèm ví dụ giúp các em dễ dàng hình dung.

Dạng 1 - Xác định hàm số y = ax^2 + bx + c

Chúng ta thực hiện giải theo các bước như sau:

• Đầu tiên gọi hàm số cần tìm là y = ax^2 + bx + c (với a khác 0)
• Tiếp đó dựa theo giả thiết ở đề ra để thiết lập mối tương quan và giải hệ phương trình theo ẩn a, b, c.
• Cuối cùng kết luận hàm số bậc 2 cần tìm.

Bài tập ứng dụng

Cho hàm số y = -0,00188(x - 251,5)^2 + 118 và yêu cầu các em:

1. Viết công thức xác định của hàm số y
2. Xác định bậc của hàm số đã cho bằng bao nhiêu?
3. Xác định hệ số của x^2, hệ số của x và hệ số tự do?

Giải:

1. Ta có y = -0,00188(x - 251,5)^2 + 118

⇔ y = -0,00188(x^2 - 503x + 63252,25) + 118

⇔ y = -0,00188x^2 + 0,94564x - 118,91423 + 118

⇔ y = -000188x^2 + 0,94564x - 0,91423

Vậy kết luận công thức của hàm số y sẽ có dạng là y = -000188x^2 + 0,94564x - 0,91423.

2. Dựa theo kết quả của 1) thì đa thức -000188x^2 + 0,94564x - 0,91423 có bậc là 2.

3. Trong đa thức: y = -000188x^2 + 0,94564x - 0,91423 ta có:

• Hệ số x^2 là -000188
• Hệ số x là 0,94564
• Hệ số tự do là - 0,91423

Dạng 2 - Lập bảng biến thiên và vẽ đồ thị hàm số bậc 2

Cho hàm số y = ax^2 + bx + c (a khác 0) ta sẽ thực hiện các bước lập bảng biến thiên và vẽ đồ thị như sau:

• Đầu tiên tìm tọa độ đỉnh I (-b/2a; -????/4a)
• Sử dụng công thức x = -b/2a để tìm trục đối xứng của đồ thị
• Tiếp theo là tìm hoành độ và tung độ của các điểm mà đồ thị giao nhau với trục hoành và trục tung (nếu có). Ngoài ra có thể tìm thêm điểm cắt, điểm đối xứng.
• Cuối cùng tiến hành vẽ đồ thị hàm số bậc 2 theo các điểm đã xác định.

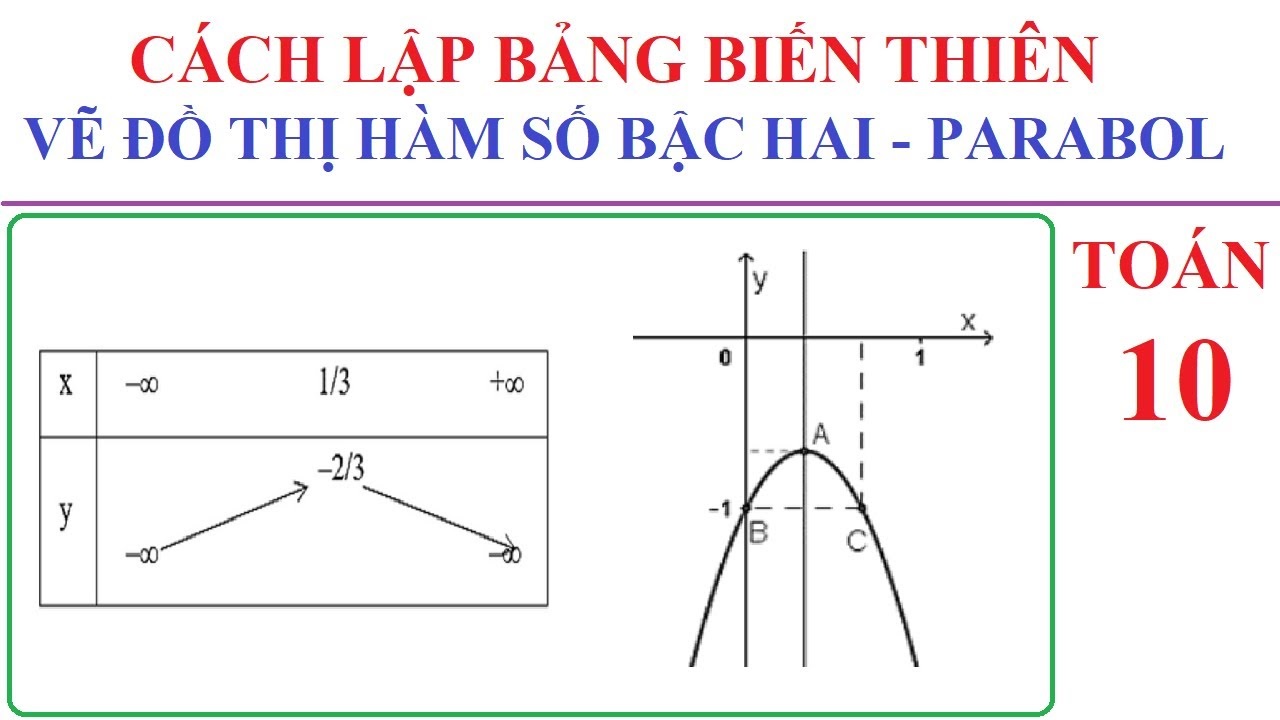Lập bảng biến thiên và vẽ đồ thị hàm số bậc 2

Bài tập ứng dụng

Vẽ đồ thị cho hàm số y = x^2 - 4x - 3

Theo đề bài ta có: a = 1, b = -4, c = -3

Áp dụng công thức tính được: ???? = (-4)^2 - 4.1(-3) = 28.

• Tọa độ đỉnh I là (2; -7)
• Trục đối xứng là x= 2
• Giao điểm của đường parabol với trục tung là A(0;-3)
• Giao điểm của đường parabol với trục hoành là điểm B(2-7; 0) và điểm C(2+7;0)
• Điểm đối xứng với điểm A (0;-3) qua x = 2 là điểm D(4;-3).

Phần lõm của parabol hướng lên trên bởi vì có a > 0.

Cuối cùng ta vẽ được đồ thị hàm số bậc 2 là y = x^2 - 4x - 3 như bên dưới:

Dạng 3 - Xác định tọa độ giao điểm hàm số bậc 2

Đối với bài toán dạng tìm tọa độ giao điểm của 2 đồ thị f(x) và g(x), các em cần giải phương trình f(x) = g(x).

• Để tìm tung độ, ta thay x vào hàm số y = f(x) hoặc y = g(x) để tính giá trị y.
• Nếu phương trình f(x) = g(x) có n nghiệm thì đồ thị của f(x) và g(x) có n điểm chung.

Bài tập ứng dụng

Cho hàm số (P) có dạng y = x^2 - 2x - 1 và đường thẳng d có dạng y = x-1. Hãy tìm tọa độ giao điểm của chúng.

Tiến hành xét phương trình hoành độ giao điểm của (P) và (d), ta có:

x^2 - 2x - 1 = -2x - 2

⇔ 2x^2 - 2x = 0

⇔ x = 1 hoặc x = 0

Với x = 0 => y(0) = 0-1 = -1

Với x = 1 => y(1) = 1-1 = 0

Kết luận tọa độ giao điểm cần tìm sẽ là (0;-1) và (1;0).

Qua bài viết này, hy vọng các em có thể nắm chắc kiến thức và hoàn thành tốt các bài tập về đồ thị hàm số bậc 2. Chúc các em có những phút giây học tập bổ ích và đừng quên theo dõi kênh thường xuyên nhé!