Cách xét dấu đa thức bậc 2 và bài tập liên quan

Dấu của đa thức bậc 2 Toán lớp 10 là một nội dung quan trọng đòi hỏi các em cần nắm lý thuyết và thường xuyên vận dụng vào bài tập.

Toán là môn học chủ chốt nhưng khá khó nhằn nên chúng ta không được lơ là bất kỳ chương nào hết. Ngày hôm nay xoilac tv sẽ thông tin đến các em học sinh những kiến thức về dấu của đa thức bậc 2 Toán lớp 10, gồm phần lý thuyết, các dạng bài tập vận dụng thường gặp, hãy cùng theo dõi chi tiết nhé!

Kiến thức về dấu của đa thức bậc 2 Toán lớp 10

Dấu của đa thức bậc hai là một nội dung quan trọng trong chương trình Toán lớp 10 mà các em cần nắm

Cho a,b,c là những hệ số cho trước và a khác 0 thì đa thức bậc hai sẽ là biểu thức có dạng ax^2 + bx + c = 0. Điển hình như: f(x) = x^2 - 4x + 5 là đa thức bậc hai. Ngược lại f(x) = x^2(2x - 7) không phải là đa thức bậc hai. Nghiệm của phương trình ax^2 + bx + c = 0 chính là nghiệm của đa thức bậc hai.

Các định lý về dấu của tam thức bậc hai

Cho đa thức bậc hai ax^2 + bx + c = 0 với a khác 0 và có ∆ = b^2 - 4ac. Đầu tiên theo định lý thuận ta có:

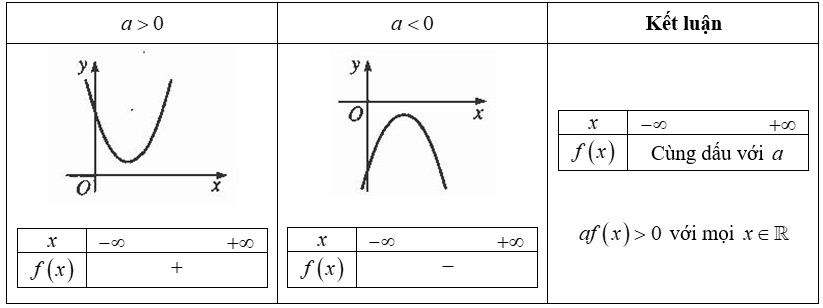
• Trường hợp ∆ > 0 thì f(x) sẽ luôn cùng dấu với a
• Trường hợp ∆ = 0 thì f(x) sẽ nhận nghiệm kép là bằng -b/2a
• Trường hợp ∆ < 0 thì f(x) sẽ có hai nghiệm x1, x2 (x1 < x2). Và f(x) cùng dấu với a khi x thuộc âm vô cùng đến x1 và x2 đến dương vô cùng. f(x) trái dấu với a khi x1< x < x2.

Các em có thể lưu ngay mẹo ghi nhớ: Khi xét dấu của đa thức bậc 2 Toán lớp 10 mà có hai nghiệm phân biệt thì sử dụng quy tắc “Trong trái, ngoài cùng”. Tức là f(x) trái dấu với trong khoảng 2 nghiệm và nếu ngoài khoảng hai nghiệm thì f(x) sẽ cùng dấu với a.

Thứ hai là theo định lý đảo dấu của đa thức bậc 2 ta có:

Tam thức bậc hai f(x) = ax^2 + bx + c = 0 với a khác 0. Nếu có số α thỏa mãn được điều kiện là α.f(α) < 0 thì lúc đó f(x) sẽ có hai nghiệm khác biệt là x1, x2 : x1 < α < x2.

Xét dấu của một đa thức bậc hai

Sử dụng máy tính tay để tính nghiệm của đa thức bậc hai rồi lập bảng xét dấu và kết luận

Các em học sinh cần lưu ý để xét dấu của đa thức bậc 2 Toán lớp 10 chúng ta thực hiện theo 3 bước sau:

• Đầu tiên là bấm máy tính ∆, tìm nghiệm của đa thức bậc hai.
• Tiếp theo lập bảng xét dấu dựa trên hệ số a.
• Cuối cùng xét dấu của đa thức bậc 2 rồi đi đến kết luận.

Ứng dụng dấu của đa thức bậc 2

Trong trường hợp a>0 và a<0 thì f(x) sẽ có đủ cả 2 loại dấu âm, dương nếu ∆ > 0. Và f(x) chỉ có 1 dấu âm hoặc dương khi ∆ < hoặc = 0. Từ đó chúng ta sẽ có:

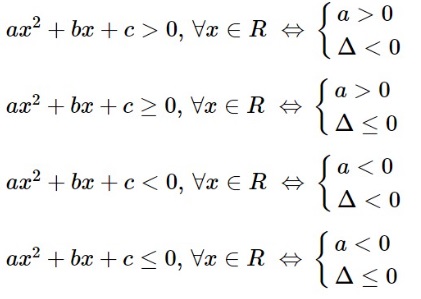
Bài tập về dấu của đa thức bậc 2 Toán lớp 10

Bài tập liên quan đến dấu của đa thức bậc hai khá đa dạng đòi hỏi phải thường xuyên luyện tập

Sau khi tìm hiểu phần lý thuyết về các định lý, cách xét dấu và ứng dụng của đa thức bậc hai. Bây giờ chúng ta sẽ cùng khám phá các dạng bài tập và bắt tay thực hành để làm tốt nội dung này nhé.

Dạng bài 1 - Giải bất phương trình bậc 2

Đây là bài tập cơ bản và các em chỉ cần áp dụng theo phương pháp:

• Biến đổi bất phương trình bậc hai về dạng một vế bằng 0 và một vế sẽ là tam thức bậc hai.
• Tiếp theo là tiến hành xét dấu vế trái tam thức bậc hai và đưa ra kết luận.

Ví dụ: Giải bất phương trình sau:

4x^2 - x + 1 < 0

Xét tam thức f(x) = 4x^2 - x + 1 ta có: ∆ = -15 < 0 và a = 4 > 0 nên f(x) > 0 với mọi x thuộc R. Từ đó suy ra bất phương trình đã cho vô nghiệm.

Dạng bài thứ 2 - Giải bất phương trình bậc hai dạng tích

• Đầu tiên chúng ta cần biến đổi cho bất phương trình bậc hai về dạng tích và thương các nhị thức bậc nhất và tam thức bậc hai.
• Sau đó tiến hành xét dấu các nhị thức bậc nhất và tam thức bậc hai đã biến đổi. Cuối cùng kết luận nghiệm đã giải ra được.

Ví dụ: Giải và biện luận bất phương trình x^2 + 2x + 6m > 0

Đặt f(x) = x^2 + 2x + 6m > 0 ta có: Δ' = 1 - 6m và a = 1, xét theo 3 trường hợp:

• Thứ nhất: Nếu Δ' < 0 tương đương m > ⅙, suy ra f(x) >0 với mọi x thuộc R.

Như vậy tập nghiệm của bất phương trình là S = R.

• Thứ hai: Nếu Δ' = 0 tương đương m = ⅙ suy ra f(x) > 0 với mọi x thuộc R \ {-1}. Như vậy S = R \ {-1}.
• Thứ 3: Nếu Δ' > 0 tương đương m < ⅙.

Dạng bài thứ 3 - Giải bất phương trình chứa ẩn ở mẫu

• Thực hiện biến đổi giải bất phương trình cho về dạng tích và thương các nhị thức bậc nhất và tam thức bậc hai.
• Sau đó xét dấu của nhị thức bậc nhất, tam thức bậc hai và kết luận nghiệm. Tuy nhiên chúng ta cần chú ý các điều kiện xác định của bất phương trình khi giải bài này.

Ví dụ: Giải bất phương trình chứa ẩn ở mẫu sau:

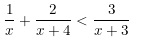
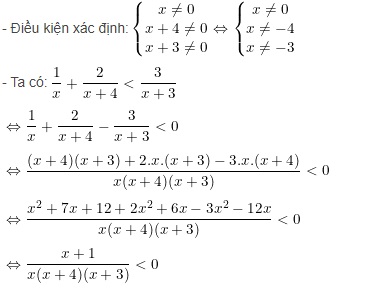
Vậy tập nghiệm của bất phương trình là S = (-12; -4) u (-3;0).

Như vậy các em đã được ôn tập lại đầy đủ về kiến thức cũng như bài tập xét dấu của đa thức bậc 2 Toán lớp 10. Chúc các em sẽ có những giây phút học tập thật vui và đạt điểm tốt trong bài kiểm tra môn Toán. Hãy cùng theo dõi kênh thường xuyên để xem thêm nhiều bài học thú vị và bổ ích nhé!