Công thức tính diện tích tam giác thường, vuông, cân, đều

Chúng ta cần ghi nhớ và hiểu rõ về công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10 để vận dụng linh hoạt vào từng đề bài đưa ra.

Để giải quyết nhanh và chính xác một bài toán, các em học sinh cần nắm vững công thức, sau đó tùy vào dữ liệu bài đưa ra để ứng dụng cho phù hợp nhất. Theo xoilac tv (kientructhienkieu.com), giữa rất nhiều kiến thức các em sẽ không tránh khỏi sự nhầm lẫn giữa tam giác thường, vuông, cân, đều,.... Vì vậy bài viết của thayphu sẽ tổng hợp đầy đủ các công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10 cho các em dễ dàng theo dõi nhé!

Tổng hợp công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10

Chỉ cần ghi nhớ và sử dụng đúng công thức thì các em sẽ nhanh chóng chinh phục được các dạng bài tính diện tích tam giác

Các bài học về diện tích tam giác rất quan trọng sẽ đi suốt chương trình học của chúng ta. Mỗi loại tam giác sẽ có công thức tính riêng và bắt buộc phải áp dụng đúng.

Công thức tính diện tích tam giác giác thường

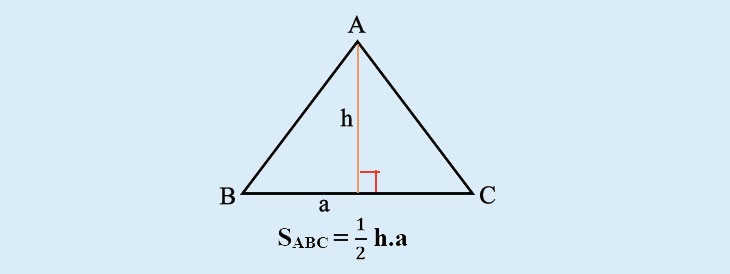
Tam giác có độ dài 3 cạnh khác nhau và số đo 3 góc khác nhau, các cạnh và các góc tạo thành 1 tam giác được gọi là tam giác thường. Ta có tam giác thường ABC, cùng các cạnh a,b,c và đường cao là ha. Như vậy diện tích tam giác sẽ bằng ½ tích chiều cao hạ từ đỉnh của tam giác tới cạnh đối diện của đỉnh đó.

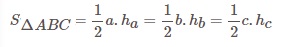
Công thức tính diện tích tam giác vuông

Tam giác với 1 góc vuông được gọi là tam giác vuông. Cách tính diện tích tam giác vuông cũng là trường hợp đặc biệt của tam giác thường khi biết 2 cạnh và góc xen giữa.

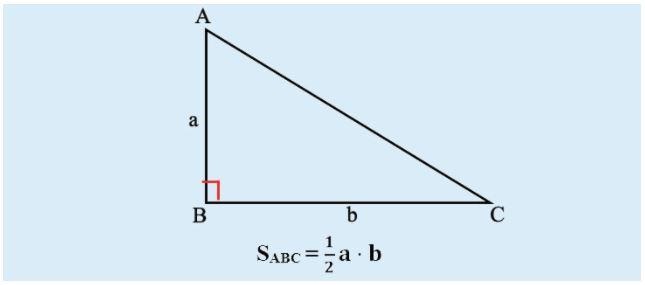
Công thức tính diện tích tam giác vuông cực kỳ đơn giản và dễ dàng ghi nhớ

Ta có công thức: S=½ a.b trong đó a, b là độ dài tương ứng của 2 cạnh góc vuông. Có thể nói công thức tính diện tích tam giác vuông khá đơn giản trong các công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10.

Công thức tính diện tích tam giác cân

Tam giác có độ dài 2 cạnh bên hoặc 2 cạnh đáy bằng nhau được gọi là tam giác cân. Diện tích tam giác cân được tính bằng một nửa chiều cao nhân cho cạnh đáy tương ứng.

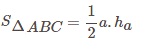
Trường hợp đặc biệt khi 2 cạnh góc vuông bằng nhau là tam giác vuông cân thì diện tích được tính bằng ½ a2. Trong đó a là độ dài của cạnh góc vuông cân.

Công thức tính diện tích tam giác đều

Tam giác thường nhưng có độ dài 3 cạnh bằng nhau và tất cả các góc trong tam giác đều bằng 60 độ thì được gọi là tam giác đều. Như vậy diện tích tam giác đều được tính theo công thức S = ½. A2. sin 60o = A2. (3 /4) với A là cạnh của tam giác đó.

Các em hãy nhớ lưu lại công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10 và học thuộc nhé.

Các dạng bài tập liên quan đến tính diện tích tam giác

Áp dụng ngay các công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10 vào bài tập

Sau khi học lý thuyết chắc chắn các em phải bắt tay thực hành các bài tập thì mới có thể dễ dàng hiểu bài được. Vậy nên đừng bỏ qua một số dạng bài tập được liệt kê ngay bên dưới đây:

Bài 1 - Tính diện tích tam giác trong hệ tọa độ Oxyz

Diện tích tam giác trong hệ trục tọa độ Oxyz sẽ có công thức riêng là SABC= ½ [AB;AC]. Trước tiên chúng ta phải tính được [AB;AC]. Cho tọa độ điểm A là A (a1, b1, c1); tọa độ điểm B là B (a2, b2, c2); tọa độ điểm C là C (a3, b3, c2). Ta có, AB = (a2-a1; b2-b1; c2-c1); AC = (a3-a1; b3-b1; c3-c1).

Như vậy chúng ta sẽ có cách tính: [AB;AC]= ( b2−b1 c2−c1) b3−b1 c3−c1 ; c2−c1 a2−a1 c3−c1 a3−a1; ; a2−a1 b2−b1 a3−a1 b3−b1 )

Cuối cùng chúng ta trừ chéo từng biểu thức cho nhau sẽ ra kết quả của [AB;AC] là tọa độ gồm 3 điểm.

Ví dụ: Trong hệ trục tọa độ Oxyz cho trước 3 điểm D (1;2;1), E (2;-1;3), F (5;2;-3). Bài toán yêu cầu tính diện tích tam giác trong hệ trục tọa độ?

DE = (1; -3; 2); DF = (4; 0; -4)

[DE;DF]= ( −3 2 0 −4 ; 2 1 −4 4 ; 1 −3 4 0 ) = (10; 12; 13)

Suy ra S DEF= ½ [DE;DF] = ½. 102+122+132 = 413/2

Bài 2 - Tính diện tích tam giác biết độ dài 3 cạnh và đường tròn ngoại tiếp

Khi đọc đề bài chúng ta phải hết sức lưu ý và xác định nên áp dụng công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10 nào phù hợp. Trong trường hợp này, diện tích tam giác sẽ tính bằng tích độ dài 3 cạnh, chia cho 4 lần bán kính (4R) của đường tròn ngoại tiếp tam giác.

Chúng ta cũng có thể áp dụng công thức Hê - rông như sau: S ABC= pp−ap−b(p−c). Với abc sẽ là độ dài của 3 cạnh và p là nửa chu vi của tam giác đó.

Vừa rồi là tổng hợp các kiến thức và bài tập liên quan đến công thức tính diện tích tam giác thường, vuông, cân, đều lớp 10. Chúc các em học sinh áp dụng thành công, hoàn thành tốt các dạng bài và nâng cao điểm số môn Toán nhé!