Modun số phức, công thức và phương pháp giải bài tập hiệu quả

Modun số phức dạng bài toán min, max thường được sử dụng rất nhiều trong các bài thi THPT quốc gia. Được tiếp cận cuối cùng trong chương trình toán học.

Modun số phức đang là một trong những chương trình đại số được tìm kiếm nhiều nhất hiện nay. Bởi nó đã xuất hiện rất nhiều trong những bài thi THPT và các bạn học sinh cùng mong muốn tìm hiểu các dạng bài tập về nó. Dưới đây Thayphu sẽ hướng dẫn các em hiểu hơn về bài học này nhé!

Khái niệm số phức

Hiểu rõ về số phức để vận dụng vào modun

Đây là một trong những con số có sự khác biệt về cách viết trong cấu tạo của các con số còn lại.

Cấu tạo số phức

Số phức sẽ được ký hiệu như sau: Z = ( a+bi) ta có a,b là số thực với:

a: là phần thực

b: là phần ảo của số phức

i: đơn vị ảo (i^2= -1)

Như vậy có thể hiểu rằng trong số phức cấu tạo khi i^2 cũng có thể bằng -1.

Ví dụ: Z= 1+2i thì ta có thể nói rằng 1 là phần thực số phức

2 là phần ảo của số phức

i là một đơn vị ảo

Số phức là gì?

• Số thuần ảo: là số chỉ có phần ảo mà không có những phần khác và không có phần thực. Lúc này ta có thể hiểu được phần thực sẽ bằng 0
• Số thực: là khi không còn phần ảo nữa lúc này hệ số ảo sẽ bằng 0
• Hai số phức bằng nhau khi đồng thời cả phần thực và phần ảo phải bằng nhau.

Xết khái niệm và cấu tạo modun số phức

Hãy học thuộc những công thức và tính chất của modun

Xét Z=a+bi cho điểm biểu diễn M(a,b) thì ta cần phải nhớ những khái niệm sau:

Số phức liên hợp được ký hiệu là = a-bi

Modun của số phức được ký hiệu 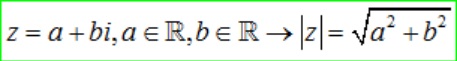. Như vậy modun số phức chính là trị tuyệt đối của số phức.

Ví dụ: Cho modun số phức sau:

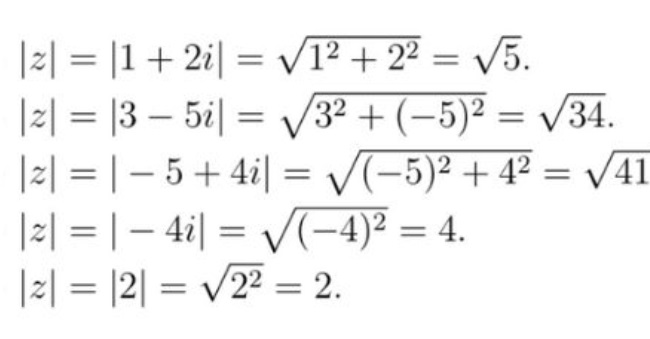
Modun số phức về mặt hình học:

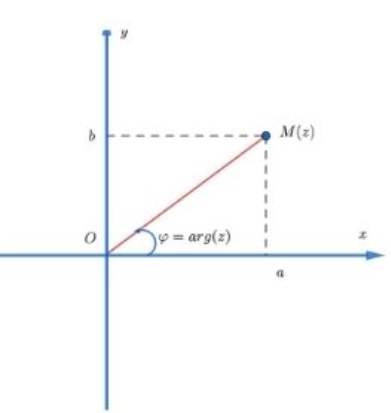
Mỗi số phức z = a + bi (với a, b thuộc R) có thể được đại diện bởi một điểm M(z) = (a, b) trên mặt phẳng Oxy và ngược lại. Modun của z có thể được biểu diễn bằng độ dài của đoạn thẳng OM(z). Modun của z là một số thực không âm và chỉ bằng 0 khi z = 0.

Những tính chất cơ bản của modun số phức

Ta có thấy được những tính chất cơ bản sau của modun số phức:

khi |z|=|-z| tức là hai số phức đối nhau sẽ có modun bằng nhau

|a+bi|=|a-bi| là hai số phức liên hợp có modun bằng nhau

Modun của Z bằng 0 ⇔ z=0

Tích hai số phức liên hợp bằng bình phương modun được thể hiện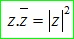

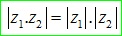moodun của một tích sẽ được bằng tích của các modun

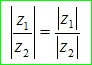modun của 1 thương sẽ bằng với thương của các modun

Bất đẳng thức của modun số phức

Modun số phức chính là độ dài đoạn thẳng trong mặt phẳng cho nên từ các bất đẳng thức của tam giác ta có thể suy ra được các bất đẳng thức modun. Dưới đây chính là các bất đẳng thức của modun:

• Bất đẳng thức cho biết rằng tổng của hai cạnh bất kỳ trong tam giác luôn lớn hơn cạnh còn lại ta có :

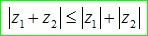
Lúc này dấu bằng sẽ xảy ra khi: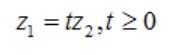

• Từ các bất đẳng thức tam giác đã được đề cập ở trên, chúng ta có thể suy ra được những điều sau đây:

Dấu bằng sẽ xảy ra khi: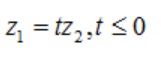

Từ hai điều trên ta có thể biểu diễn biểu đồ lần lượt là:

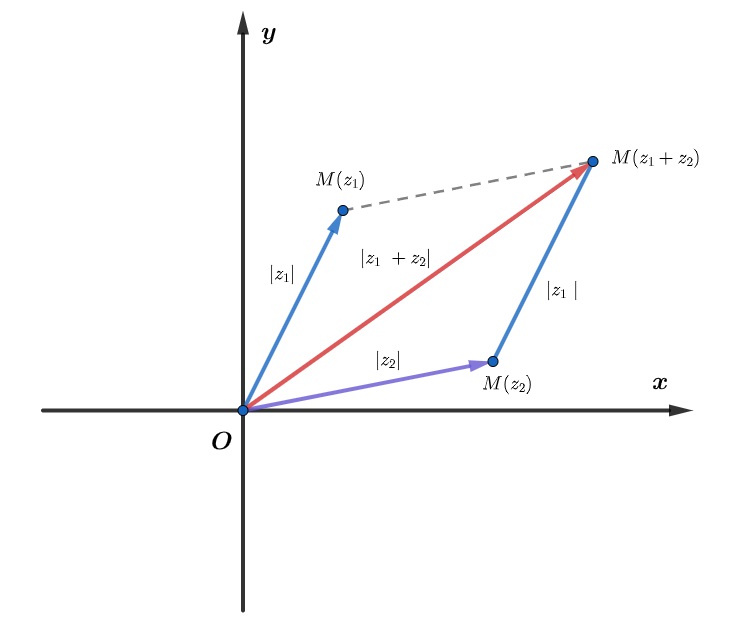
Biểu đồ biểu diễn khi tổng của hai cạnh bất kỳ trong tam giác luôn lớn hơn cạnh còn lại

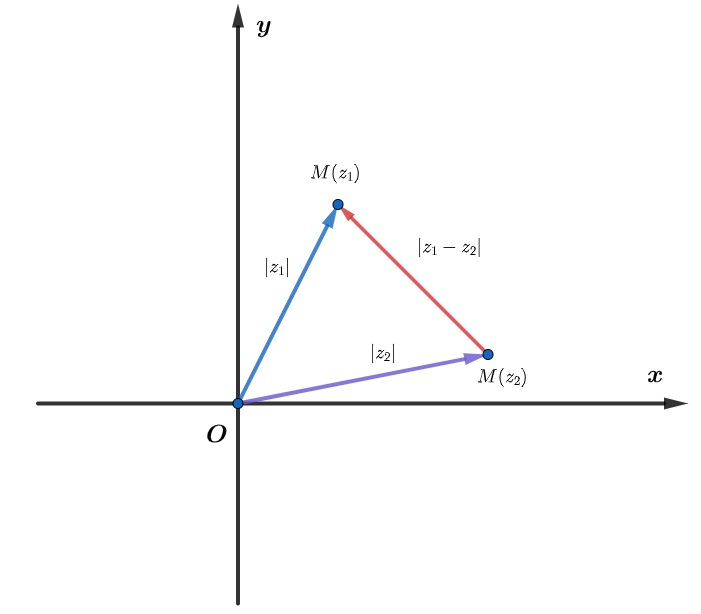
Biểu đồ thể hiện công thức số của modun

• Có thể dùng bất đẳng thức tam giác để suy ra các bất đẳng thức sau đây: "Hiệu của hai cạnh trong một tam giác luôn nhỏ hơn cạnh thứ ba".

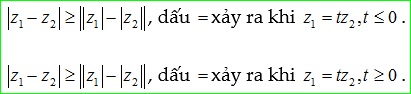
Các dạng bài tập về modun số phức

Các dạng bài tập về modun số phức thường khá là đơn giản dễ dàng tiếp cận. Tuy nhiên, nó bắt buộc các bạn phải hiểu được bản chất của bài. Vậy nên, dưới đây là một số dạng bài tập thường hay gặp trong những bài thi:

Bài tập 1: Tìm modun số phức của z= 1+4i+(1-i)^3

Lời giải

Ta có: (1-i)^3 = 1^3 - 3i + 3i^2-i^3

= 1-3i-3+i = -2-2i => z= 1+4i+(1-i)^3 = 1+4i - 2-2i = -1+2i

Vậy modun số phức sẽ bằng :|z|= √(-1)^2+ (2)^2 = √5

Bài tập 2: Tính môđun của số phức của hàm số sau z = 6 – 8i

Lời giải:

Ta có z= 6-8i => modun sẽ bằng |z| = √ 6^2 + (-8)^2 = 10

Bài tập 3: Tính modun số phức 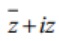khi biết z thỏa mãn :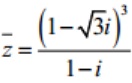

Lời giải

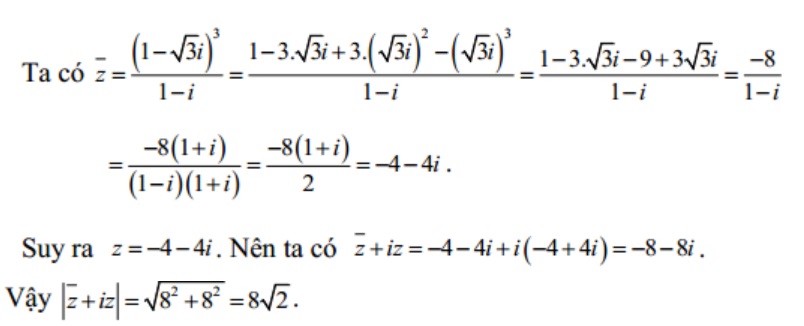
Bài tập 4: Cho số phức z thỏa mãn: 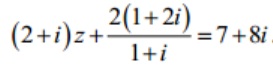hãy tìm modun số phức w= z+1+i

Lời giải

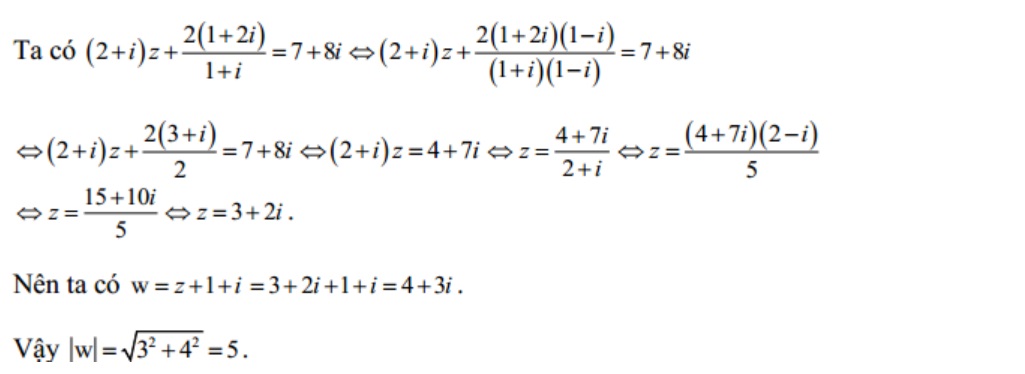
Bài tập 5: Cho số phứ z thỏa mãn : 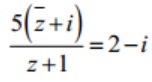. Hãy tính modun số phức .

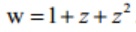Lời giải

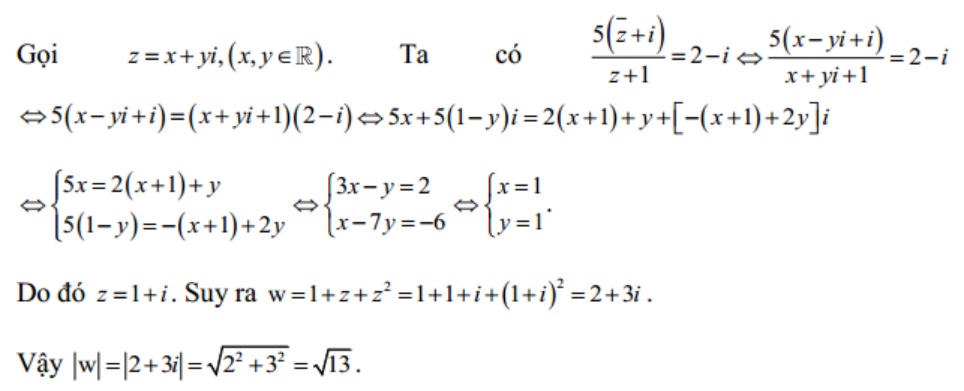
Bài tập 6: tìm số phức z khi thỏa mãn: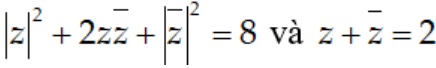

Lời giải

|z|^2 + 2zz +z^2=> ta có 4(x^2 + y^2 ) = 8 → x^2 + y^2 = 2

từ đó ta có thể => x=1 và y1= -1, y2= 1

Vận dụng lý thuyết giải bài tập về nhà

Bài 1: Cho số phức z = 2 - 3i. Tính modun số phức

Bài 2: Cho hai số phức z1 = 4 + 3i ; z2 = 2 - 3i Tính P = |z1 + z2|

Bài 3: Cho số phức z = (5-6i)(3+i)^2. Môđun của w = iz + z

Bài 4: Giả sử có một số phức z thỏa mãn điều kiện:

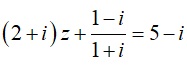
Hãy tính modun của số phức w = 1 + 2z + z^2

Bài 5: Cho số phức z = 7 - 3i. Tính modun số phức này.

Kết luận

Bài viết trên là những tổng hợp lý thuyết về dạng bài modun số phức. Về cơ bản dạng bài tập này khá đơn giản và dễ dàng áp dụng. Vậy nên hãy học thuộc thật kỹ và nắm chắc kiến thức về modun. Hy vọng rằng bài viết mà thayphu cung cấp sẽ giúp các em dành được điểm cao hơn trong kỳ thi THPT.