Công thức bất đẳng thức toán lớp 10 và bài tập vận dụng

Công thức bất đẳng thức có liên quan đến hầu hết các bài tập. Nắm vững phần lý thuyết sẽ giúp các em hoàn thành tốt nhiều dạng đề.

Công thức bất đẳng thức được xem là một trong kiến thức quan trọng, liên quan đến nhiều dạng bài tập trong môn Toán. Bài viết sau đây sẽ tổng hợp đầy đủ các thông tin giúp các em dễ dàng nắm vững. Đặc biệt không thể thiếu các ví dụ minh họa dễ hiểu, hãy cùng thayphu theo dõi ngay nhé!

Khái niệm về bất đẳng thức

Kiến thức cơ bản về bất đẳng thức

Bất đẳng thức thường có các dạng như A > B, A < B, A >= B, A <= B chính là một mệnh đề xác định. Như vậy A được gọi là vế trái của bất đẳng thức và B là vế phải của bất đẳng thức. Với A, B là những biểu thức có chứa số và phép toán. Từ đó ta có hệ quả:

• Trường hợp A < B => C < D được xác định là mệnh đề đúng thì bất đẳng thức C < D là bất đẳng thức hệ quả của bất đẳng thức A < B.
• Trường hợp A < B => C < D và C < D => A < B đều là mệnh đề đúng thì 2 bất đẳng thức A < B và C < D có giá trị tương đương nhau.

Tính chất của bất đẳng thức

Trước khi áp dụng công thức bất đẳng thức, các em không thể qua các tính chất thường gặp của bất đẳng thức như:

• Tính chất bắc cầu: Ví dụ nếu như cùng lúc có 2 biểu thức A < B và B < C thì có thể suy ra ngay A < C.
• Cộng 2 vế của bất đẳng thức với cùng 1 số. Điều này khá đơn giản chỉ cần nhớ: A < B ⇔ A + C < B + C
• Cộng 2 bất đẳng thức cùng chiều, nếu đề cho 2 bất đẳng thức cùng chiều là A < C và B < D ta sẽ có: A + C < B + D
• Nhân 2 vế của bất đẳng thức với 1 số, khi cho A < B và C > 0 ta có AC < BC. Ngược lại nếu A < B và C < 0 ta có AC > BC.
• Nhân 2 vế của bất đẳng thức cùng chiều. Đề ra 0 < A < B và 0 < C < D thì có ngay kết quả là AC < BD.

Tổng hợp các công thức bất đẳng thức

Bất đẳng thức Cô-si

Bất đẳng thức Cô-si hay còn được là bất đẳng thức trung bình cộng, trung bình nhân hay AM - GM.

Công thức bất đẳng thức Cô-si cho a và b với điều kiện a, b không âm có dạng:

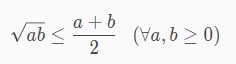
Lúc này dấu = chỉ xảy ra a = b. Từ đó ta có bất đẳng thức Cô-si cho 3 số a, b, c không âm như sau:

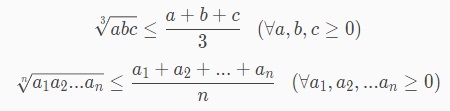
Theo đó, nếu 2 số dương bất kỳ có tổng không đổi thì tích của 2 số này sẽ lớn nhất nếu giá trị 2 số bằng nhau. Trường hợp 2 số dương xác định có tích không đổi thì tổng của 2 số nhỏ nhất khi giá trị 2 số bằng nhau.

Công thức bất đẳng thức chứa giá trị tuyệt đối

Các em có thể áp dụng một số bất đẳng thức chứa dấu giá trị tuyệt đối này để giải các dạng toán bất đẳng thức nâng cao.

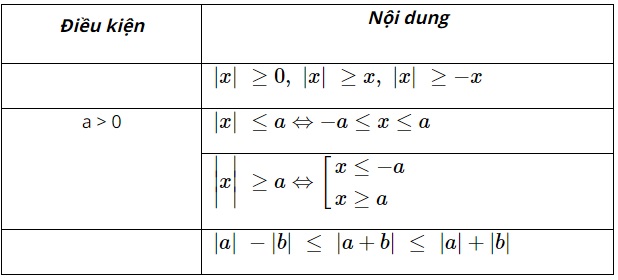
Bất đẳng thức chứa dấu giá trị tuyệt đối

Bất đẳng thức tam giác

Cho a,b, c là 3 cạnh trong tam giác, ta sẽ có các bất đẳng thức tam giác như sau:

• a > 0, b > 0, c > 0
• |b - c| < a < b + c
• |c - a| < b < c + a
• |a - b| < c < a + b

a > b > c ⇔ A > B > C với A, B, C lần lượt là các góc đối diện của các cạnh a, b, c.

Các dạng toán liên quan đến công thức bất đẳng thức

Bất đẳng thức là nội dung xuất hiện khá nhiều trong chương trình THCS và THPT. Vậy nên sau khi nắm về lý thuyết, các em hãy cùng tham khảo các dạng bài tập liên quan để hiểu rõ.

Dạng 1: Áp dụng bất đẳng thức Cô-si

Lưu khi áp dụng công thức bất đẳng thức Cô-si:

• Các số trong đó phải là những số không âm.
• Bất đẳng thức theo đề ra có tổng và tích
• Điều kiện khi xảy ra dấu = đó là các số bằng nhau

Ngoài ra bất đẳng thức Cô-si còn có hình thức khác thường dùng với 2 số: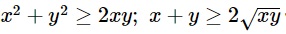

(điều kiện với mọi x,y >= 0)

Với 3 số:

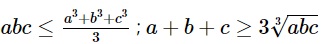
(điều kiện với mọi a,b,c >=0)

Bài tập ứng dụng

Cho 3 số thực dương x, y, z. Các em hãy chứng minh rằng: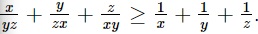

Giải:

Bởi các số x, y, z là các số thực dương nên ta có

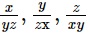cũng là các số dương.

Theo công thức bất đẳng thức Cô-si ta được:

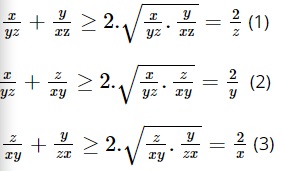
Cộng các vế (1), (2), (3) kết quả là:

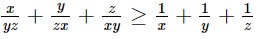
Như vậy dấu = xảy ra khi và chỉ khi x = y = z.

Dạng 2: Chứng minh bất đẳng thức dựa vào định nghĩa

Để chứng minh bất đẳng thức A >= B (hoặc A > B) đầu tiên ta xét hiệu A - B. Tiếp tục sử dụng linh hoạt kiến thức để chứng minh A - B >= 0 hoặc A - B > 0. Cuối cùng kết luận và xét A = B trong trường hợp nào.

Bài tập ứng dụng

Cho a, b > 0 và hãy chứng minh rằng

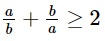
Do a, b > 0 nên ta có:

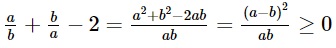
Vì vậy:

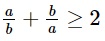
Lúc này dấu = xảy ra khi và chỉ khi a = b.

Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của 1 đại lượng

Khi gặp dạng bài này chúng ta cần vận dụng tính chất, công thức bất đẳng thức Cô-si, công thức bất đẳng thức chứa dấu giá trị tuyệt đối,... Từ đó tìm ra các giá trị lớn nhất, giá trị nhỏ nhất.

Bài tập áp dụng

Tìm giá trị nhỏ nhất của biểu thức bên dưới:

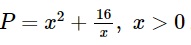
Theo bài ra ta có:

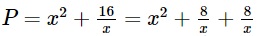
Áp dụng bất đẳng thức Cô-si 3 số ta được

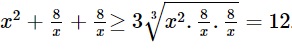
Như vậy giá trị nhỏ nhất của P sẽ là 12.

Dấu = xảy ra trong trường hợp x = 2.

Với những kiến thức lý thuyết về công thức bất đẳng thức và bài tập chia sẻ ở trên hy vọng các em có thể chinh phục chủ đề này và đạt nhiều điểm tốt. Đừng quên theo dõi kênh để cập nhật nhiều bài học hay và hữu ích nhé!