Cách vẽ đồ thị Parabol chi tiết và chính xác nhất

Hướng dẫn cách vẽ đồ thị Parabol chi tiết và chính xác nhất. Các bài tập vận dụng liên quan kèm lời giải đơn giản và dễ hiểu.

Lý thuyết và bài tập về cách vẽ đồ thị Parabol chính là kiến thức quan trọng trong chương trình Toán lớp 10. Và đây cũng là kiến thức sẽ có trong các đề thi THPT. Chính vì vậy các em cần nắm vững và giải thành thạo các bài toán. Bài viết sau đây của thayphu sẽ cung cấp đầy đủ các thông tin chính xác và dễ hiểu, hãy cùng tham khảo ngay nhé!

Cách vẽ đồ thị Parabol bằng dụng cụ thước kẻ và compa

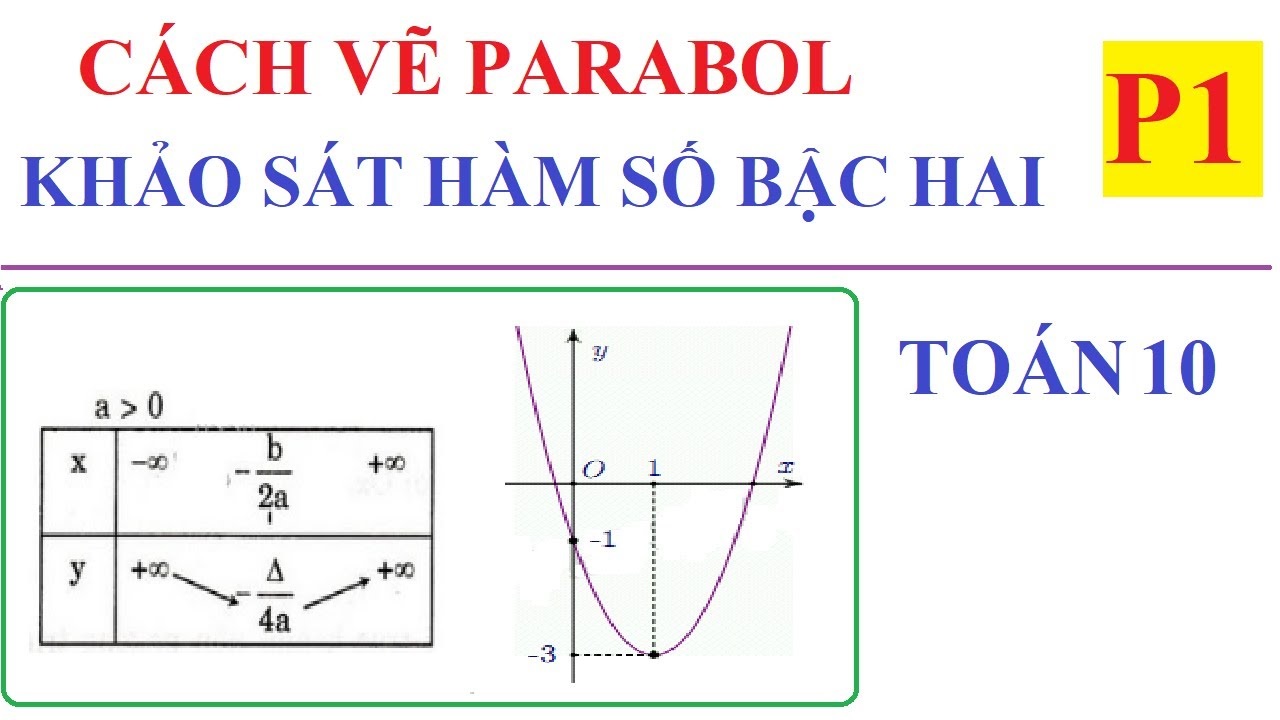
Cách vẽ đồ thị hàm số bậc 2 chi tiết và chính xác

Cách này được áp dụng khá phổ biến nhờ thuận tiện và dễ dàng.

Bước 1: Tiến hành khảo sát các điểm có trên parabol. Các điểm đối xứng với nhau qua trục nên có thể khảo sát một bên của parabol.

Bước 2: Ta kẻ trục Ox vuông góc với trục Oy tại điểm O.

Bước 3: Trên trục Ox, xác định 2 điểm E và M, sao cho điểm M là trung điểm của OE. Tức là OM = OE.

Bước 4: Tìm điểm M’ bất kỳ trong ME và dùng thước thẳng kẻ một đường đi qua M’. Đồng thời phải song song với đường thẳng đã biết.

Bước 5: Sử dụng compa quay đúng 1 vòng cung với bán kính bằng kích thước đoạn OM’. Điểm thuộc parabol chính là điểm cắt giữa cung và nằm trên đường thẳng song song với OM.

Bước 6: Chọn thêm các điểm bất kỳ thuộc ME, dùng thước nối các điểm lại với nhau để được parabol hoàn chỉnh.

Cách vẽ đồ thị Parabol bằng hàm bậc 2

Bước 1: Tìm điểm tọa độ của đỉnh parabol là (-b/2a; -Δ/4a)

Bước 2: Tìm trục đối xứng đi qua đỉnh và song song với trục tung là x = -b/2a

Bước 3: Tìm tọa độ các giao điểm của parabol với trục tung là điểm (0; c) và trục hoành nếu có.

Tìm thêm các điểm khác như những điểm đối xứng với điểm (0; c) qua trục đối xứng của parabol sẽ giúp vẽ parabol chính xác hơn.

Bước 4: Dựa vào tính chất đối xứng, xác định bề lõm, hình dạng của parabol để nối các điểm lại và hoàn thành đồ thị.

Chú ý:

Hàm số bậc 2 có dạng là y = ax^2 + bx + c (với a khác 0)

Trong đó a, b, c là các hằng số. Đồ thị của hàm số bậc 2 là một đường cong hình chữ U được gọi là parabol. Trong đồ thị, đường parabol hướng lên hay xuống phụ thuộc vào hằng số a.

• Nếu a < 0 thì bề lõm đường parabol quay xuống dưới
• Nếu a > 0 thì bề lõm đường parabol quay lên trên.

Độ chính xác của đồ thị phụ thuộc vào lượng nhiều hay ít của các điểm. Vì vậy chúng ta có thể tìm nhiều điểm khác nhau cho đồ thị.

Các đặc điểm của parabol

Đầu tiên là đỉnh parabol. Khi parabol hướng lên trên thì đỉnh sẽ biểu diễn điểm thấp nhất trên đồ thị. Hoặc giá trị nhỏ nhất của hàm số. Khi parabol hướng xuống, đỉnh biểu thị điểm cao nhất trên đồ thị. Hoặc giá trị lớn nhất của hàm số.

Trục đối xứng parabol. Parabol nào cũng sẽ có trục đối xứng và luôn song song với trục y. Trục đối xứng là một đường thẳng đứng vẽ đi qua đỉnh.

Giao điểm y là điểm mà tại đó parabol đi qua trục y. Và chỉ có một điểm như vậy đối với đồ thị của hàm số bậc 2. Nếu có thì đường cong sẽ không phải một hàm. Vì có hai y cho một x bằng 0.

Bài tập vận dụng

Bài 1

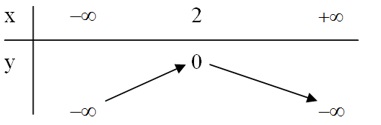
Lập bảng biến thiên và vẽ đồ thị của hàm số y = -x^2 + 4x - 4

Với hàm số y = -x^2 + 4x - 4 ta sẽ có:

Tập xác định là tập R

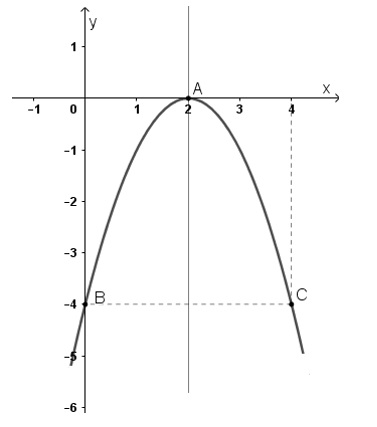
Đỉnh I có tọa độ là (2; 0)

Đường thẳng x = 2 chính là trục đối xứng

Giao điểm với trục hoành là điểm A (2;0)

Giao điểm với trục tung là điểm B (0; -4)

Điểm đối xứng với điểm B(0; -4) qua đường thẳng x = 2 là điểm C(4; -4).

Lập bảng biến thiên:

Tiến hành vẽ đồ thị hàm số như sau:

Bài 2

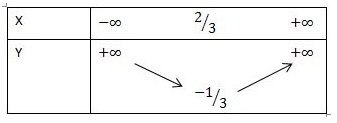
Lập bảng biến thiên và vẽ đồ thị cho hàm số y = 3x^2 - 4x + 1

Với hàm số y = 3^2 - 4x + 1 ta có: a = 3; b = -4; c = 1

Tập xác định là D = R

Điểm I (2/3 ; -1/3 ) là tọa độ đỉnh

Đường thẳng x = ⅔ là trục đối xứng

Xét tính biến thiên:

Vì a = 3 > 0 nên hàm số nghịch biến trên khoảng (âm vô cùng; ⅔) và đồng biến trên khoảng (⅔; dương vô cùng)

Lập bảng biến thiên

Đồ thị giao trục hoành y = 0 với x = 1 và x = ½

Đồ thị giao trục tung: x = 0 => y = 1

Như vậy đồ thị hàm số y = 3x^2 - 4x + 1 là đường parabol có:

Đỉnh I (⅔; -⅓), trục đối xứng là x = ⅔ nên parabol quay bề lõm lên trên.

Bài tập tự luyện

Bài 1: Vẽ đồ thị của hàm số y = 2x^2 - 7x + 4 và xét tính đồng biến, nghịch biến của nó trên tập xác định.

Bài 2: Vẽ đồ thị của hàm số y = -3x^2 - 5x + 3 và xét tính đồng biến, nghịch biến của nó trên tập xác định.

Vừa rồi là hướng dẫn cách vẽ đồ thị Parabol, bài tập vận dụng và lời giải chi tiết. Các em đừng quên thực hành cùng các bài tập tự luyện để nắm vững và thành thạo nội dung này nhé!